屋盖结构的风振分析及等效静风荷载研究

马 超，石碧青

(华南理工大学土木与交通学院，广东广州 510641)

屋盖结构的风振分析及等效静风荷载研究

马 超，石碧青

(华南理工大学土木与交通学院，广东广州 510641)

结合刚性屋盖模型的风洞试验，在采用HEM方法精确分析结构风致响应的基础上，根据位移等效原则，结合荷载响应相关法(LRC)可以计算出大跨度屋盖空间结构的等效静风荷载(ESWL)，并将其应用于某体育场馆的风振分析和ESWL计算，结果显示了该方法的有效性和正确性。

风洞试验；大跨度屋盖；风致响应；风荷载

由于大跨度屋盖空间结构具有自重轻、阻尼小、柔性大、自振频率低等特点，对风荷载非常敏感，因此，风荷载往往是这类结构的主要控制荷载。如果运用随机振动理论来进行结构设计，计算过程将会十分复杂，因此，为便于结构设计人员的计算分析，工程上采用等效静风荷载来计算屋盖结构的风致响应。所谓的等效静风荷载，是指将该荷载作为静力荷载作用在结构上时，它所引起结构的某一响应与实际风荷载作用时该响应的最大值一致。

DAVENPORT根据阵风荷载因子法(GLF)将动力学问题转化为静力分析[1]，最早提出了等效静风荷载的概念，该方法也编入了包括中国在内的许多国家的高层建筑设计规范，由于GLF法具有简单快捷的优点，早期也被许多科研人员用来研究大跨度屋盖结构的风振分析。KASPERSKI等在1992年提出了荷载响应相关法(load-response-correlation，即LRC)，该方法物理意义明确，但并未考虑共振部分，只能计算背景响应，因此只适用于刚性屋盖结构[2]。HOLMES提出将LRC法与惯性力法相结合，将等效静风荷载分为平均风荷载、背景风荷载以及由多阶共振响应分量产生的惯性风荷载[3]。谢壮宁等在2007年提出了测点影响系数的方法，实现了测点风压系数向结点荷载的快捷转换，提高了求解效率[4]。由于传统的完全二次型组合法计算十分复杂，耗时长，占用计算机内存大，谢壮宁等提出了风致复杂结构随机振动分析的一种快速算法——谐波激励法(HEM)，并将其用于某实际工程[5-6]，该方法大大提高了计算速度并降低了计算机所耗费的内存。

由于屋盖结构会存在多阶振型参与振动，使得结构上的一些关键响应并不完全相关，针对不同的响应存在着不同的等效静风荷载形式，这给结构设计带来诸多不便。因此，如何以尽可能少的等效静风荷载来实现较多的目标等效，成为大跨度屋盖结构等效静风荷载研究中的一个重要问题。KATSUMURA等在2007年提出了一致等效静风荷载的分析方法(Universal ESWL)[7]，其基本思路为将脉动风荷载的本征模态作为等效静风荷载的基本分布模式，采用最小二乘法计算出各分布模式的最优组合系数，以满足多目标的要求。陈波等在此基础上，以风荷载的主要本征模态和结构主导振型惯性力作为基本向量来构造多目标等效静风荷载，使该方法具有一定的物理意义[8]。吴迪等根据静力学原理和风荷载各方向分量的关系分别建立多目标等效方程组和约束方程组，避免了某些不合理作用模式的出现，而且提高了计算效率[9]。多目标等效静风荷载分析方法的提出实现了以少量的等效荷载模式保证多个目标等效，但实际上，屋盖结构各节点的响应一般并不会同时达到峰值，使得这种等效方法可能会高估风荷载对结构的作用，造成不必要的浪费。所以就目前来看，具体问题具体分析并以单目标等效的大跨度屋盖结构等效静风荷载理论仍然具有较大的工程使用价值。

本研究在精确分析屋盖结构的风振响应基础上，以位移等效为原则计算了结构的等效静风荷载以及风振响应，并将其应用于某体育场馆，结果显示了该方法的有效性和合理性。

1 等效静风荷载的计算

结构在脉动风荷载作用下的响应可由如下动力学方程求得：

(1)

式中：[M]、[C]、[K]分别为结构的质量矩阵、阻尼矩阵以及刚度矩阵；{y(t)}为结构的位移；{f(t)}是作用在结构上的脉动风荷载。

根据模态展开定理，结构的弹性恢复力可表示为

{F(t)}= [K]{y(t)}=[K][Φ]{q(t)}=

[M][Φ][Λ]{q(t)}。

(2)

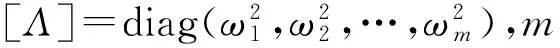
根据式(3)所求得的弹性恢复力，屋盖结构上的响应r(t)可利用影响系数表示为式(4)形式[10]:

{r(t)}=[A]{F(t)}。

(3)

式中：{r(t)}为n×1阶响应向量；[A]为影响系数矩阵(当所计算的响应是位移时，则[A]为结构的柔度矩阵)，矩阵[A]中的元素aij表示在坐标j上作用单位荷载而在杆件i中所产生的响应。响应的协方差为

[Crr]=[A][CFF][A]T。

(4)

式中：[Crr]为响应的n×n阶协方差矩阵，对角元素为响应的均方值；[CFF]为荷载的n×n阶协方差矩阵。令[D]=[M][Φ][Λ]，根据式(3)可以得到弹性恢复力的协方差矩阵为

[CFF]=[M][Φ][Λ][Cqq][D]T。

(5)

式中：[Cqq]为模态响应的m×m阶协方差矩阵，可采用HEM方法计算得到。根据以上关系，可以推出{F(t)}和{r(t)}的协方差矩阵为

[CrF]=[A][CFF]。

(6)

式中：[CrF]为响应荷载的n×n阶协方差矩阵，矩阵中的元素表示响应ri与荷载Fj的协方差。由此，根据LRC法可以得到结构产生最大响应的等效静风荷载为

(7)

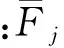
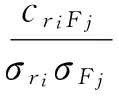
(8)

式中：σri和σFj分别为响应ri和Fj的标准差，上述等效静风荷载产生的最大响应为

(9)

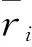
2 风洞试验

在汕头大学风洞实验室中对一个门式钢架结构的体育场馆进行了风洞试验，结构原型最大高度为36 m，檐口最低高度为23.7 m，模型的几何缩尺比为1∶150，见图1。根据有关设计部门的要求，风洞试验建筑模型的上游地貌设定为建筑结构荷载规范的B类地貌，分别取50年和100年重现期进行计算，对应的该地区基本风压为0.40 kN/m2和0.45 kN/m2，指数律地貌粗糙度α为0.16。根据试验要求，在该结构模型上共布置了347个测压点，每个测压点的样本长度为20 480个数据，采样频率为312.5 Hz。

试验采用同步多点压力扫描系统DSM3200测压，进而根据结构的动力特性分析模型，按上述方法分析结构的风振响应和节点的等效静风荷载。

图1 安装在风洞转盘上的建筑模型Fig.1 Building model in the wind tunnel

3 结果分析

3.1结构动力特性

使用SAP2000有限元软件对该屋盖进行结构模态分析，根据结构在不同振型下的变形状况，分别选取第1阶、第2阶、第7阶以及第20阶模态进行研究，相应的结构自振频率分别为0.733 1,0.942 0,1.303 8,1.834 8 Hz，屋盖的结构阻尼比为0.02，图2为该屋盖结构的有限元模型。

图2 结构的有限元模型Fig.2 Finite element model of the structure

图3为使用SAP2000计算得到的结构前几阶模态的振型。分析发现，屋盖的第1阶以及第2阶振型并非结构振动时的主导振型，这2种情况下的屋盖主要是以水平方向的振动为主，而第7阶和第20阶模态下的竖向振动则较为明显，对于大跨度屋盖的结构设计，一般以竖向振动为主要研究对象。由此可以看出，大跨度屋盖结构在风荷载作用下的振动分析要比高层结构复杂得多，屋盖的共振响应并非完全由前几阶振型主导，也可能会存在一些对振动贡献占主导地位的高阶振型，如采用传统的CQC方法来计算屋盖的响应，计算量将十分巨大。因此，本研究对屋盖风振响应的分析采用HEM法，在减少计算量和计算机所耗费内存的同时，能够保证较高的精度。

图3 体育馆在不同振型下的振动形态Fig.3 Vibration of the stadium in different modes

3.2结构气动力分布及响应的基本特征

1) 结构整体基础合力随风向角的变化

图4为结构在风荷载作用下基础底部所受到的竖向力，根据曲线上荷载大小的峰值分布情况可以看出，当风荷载沿着屋盖的对角线作用在结构上时，所受到的基底反力出现较大值，因此，这几种工况下的结构响应值得注意。

图4 结构基底反力Fig.4 Base force of the structure

2) 结构最大位移分布

图5为屋盖在不同风向角工况下的结点最大位移的精确结果与按静力学原理将等效静风荷载施加到结构上所求解到的相应位移值的对比图。由图5可知，不同工况下的2组位移值是完全一致的，这也证明了本文所述方法的有效性和正确性；同时，结合曲线中响应值大小的分布以及上述基底反力大小的分布情况，分别取风向角60°，150°，250°以及320°等工况进行研究。

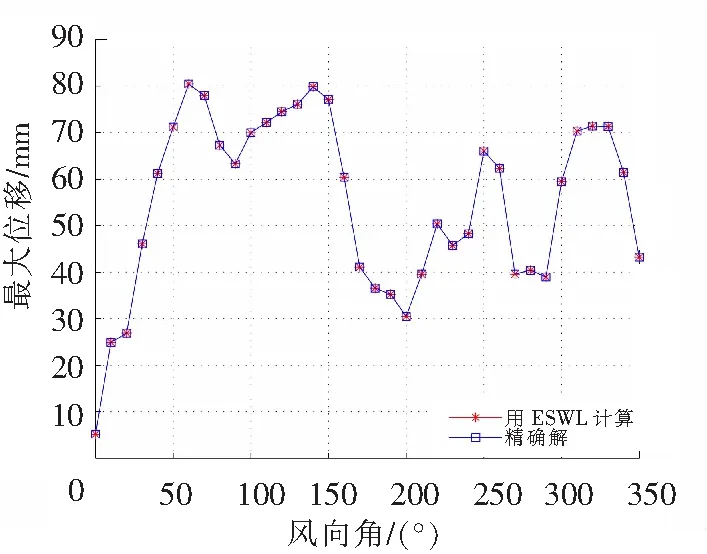
图5 不同风向角下的结点最大位移Fig.5 Maximum node displacement versus wind direction

3) 风压系数分布

以上述4个敏感风向角中的60°和150°为代表，图6为屋盖在风向角为60°和150°时B类地貌下的风压系数分布。由图6可以看出，在迎风面的结构边缘处的风压较大，且均为负压，即屋盖在边缘处承受较大的升力，而在远离迎风面的部位，其平均风压也越来越小，甚至为0。

图6 屋盖的风压系数分布Fig.6 Wind pressure coefficient distribution of the roof

3.3推荐的等效静力风荷载

由于大跨度屋盖结构存在多阶振型参与振动的特点，使得结构的一些关键响应并不完全相关，针对不同的目标响应，会有不同形式的等效静风荷载，给结构设计人员带来诸多不便。KATSUMURA等相关科研人员提出的多目标等效静风荷载计算方法，达到了以尽可能少的等效静风荷载模式完成多个目标的等效，一定程度上简化了工程设计，但同时也存在着一些问题[7]。

4 结 语

大跨度屋盖结构的振动贡献并非完全由第1阶振型主导， 往往会存在一些对振动贡献较大的高阶振型，与高层建筑的结构振动有很大的不同，使得屋盖的结构设计变得十分复杂。为此，本研究在多点同步测压的风洞试验基础上，采用HEM方法分析了大跨度屋盖空间结构的风致响应，分别以位移等效和应力等效为原则，并结合LRC法计算了结构的等效静风荷载以及相应的响应。将其用于某体育馆的风振分析，计算结果证明了该方法的有效性和正确性。同时，指出了多目标等效静风荷载分析方法所存在的一些问题。虽然该方法能够以较少的等效静风荷载模式描述多个目标的等效，简化结构设计，但该方法会高估风荷载对结构的作用，在工程上造成不必要的浪费。因此，就目前的研究状况来看，单目标等效依然是较为理想的等效静风荷载求解方法。

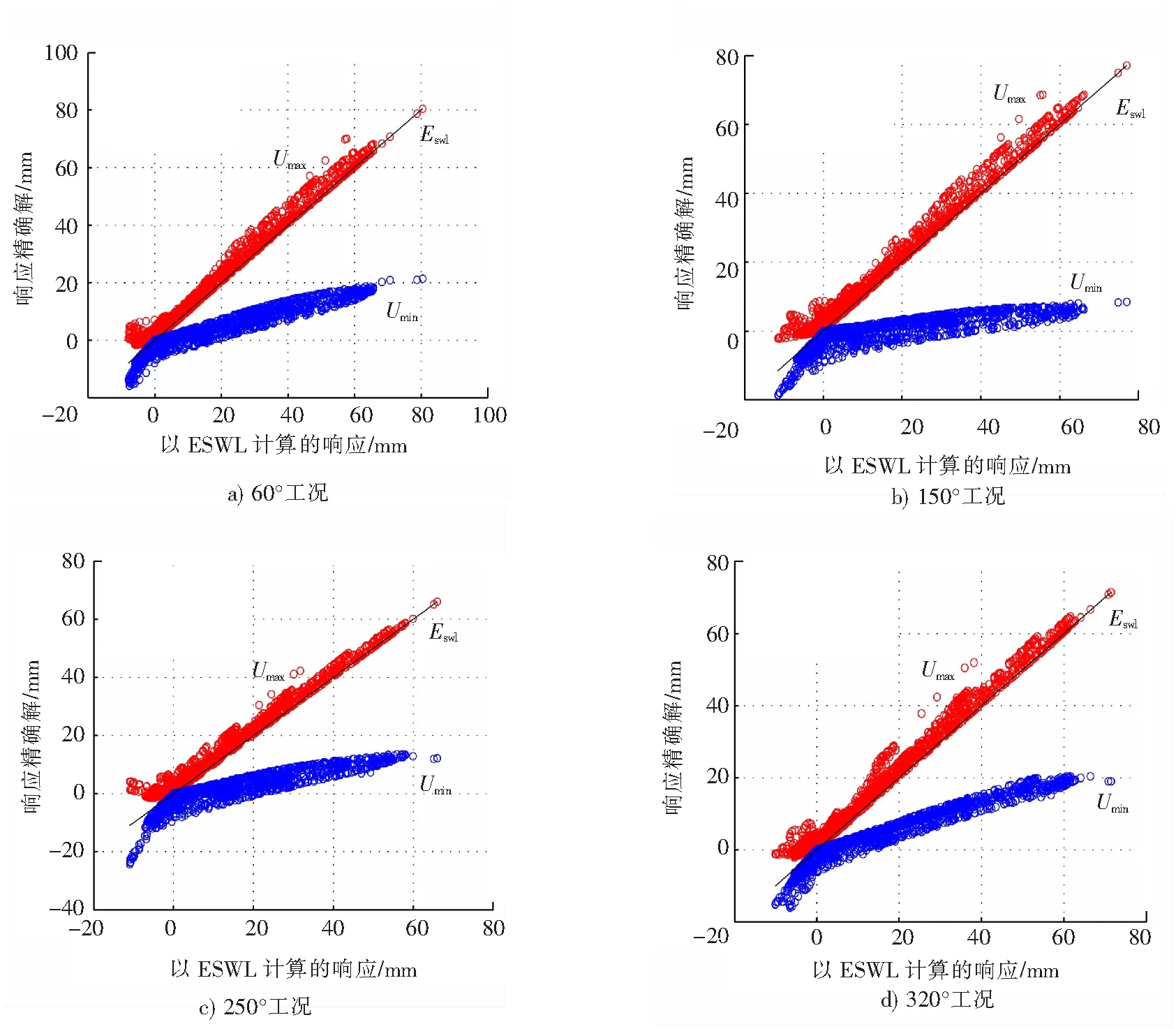
图7 屋盖各结点在不同工况下的位移Fig.7 Node displacement versus wind direction

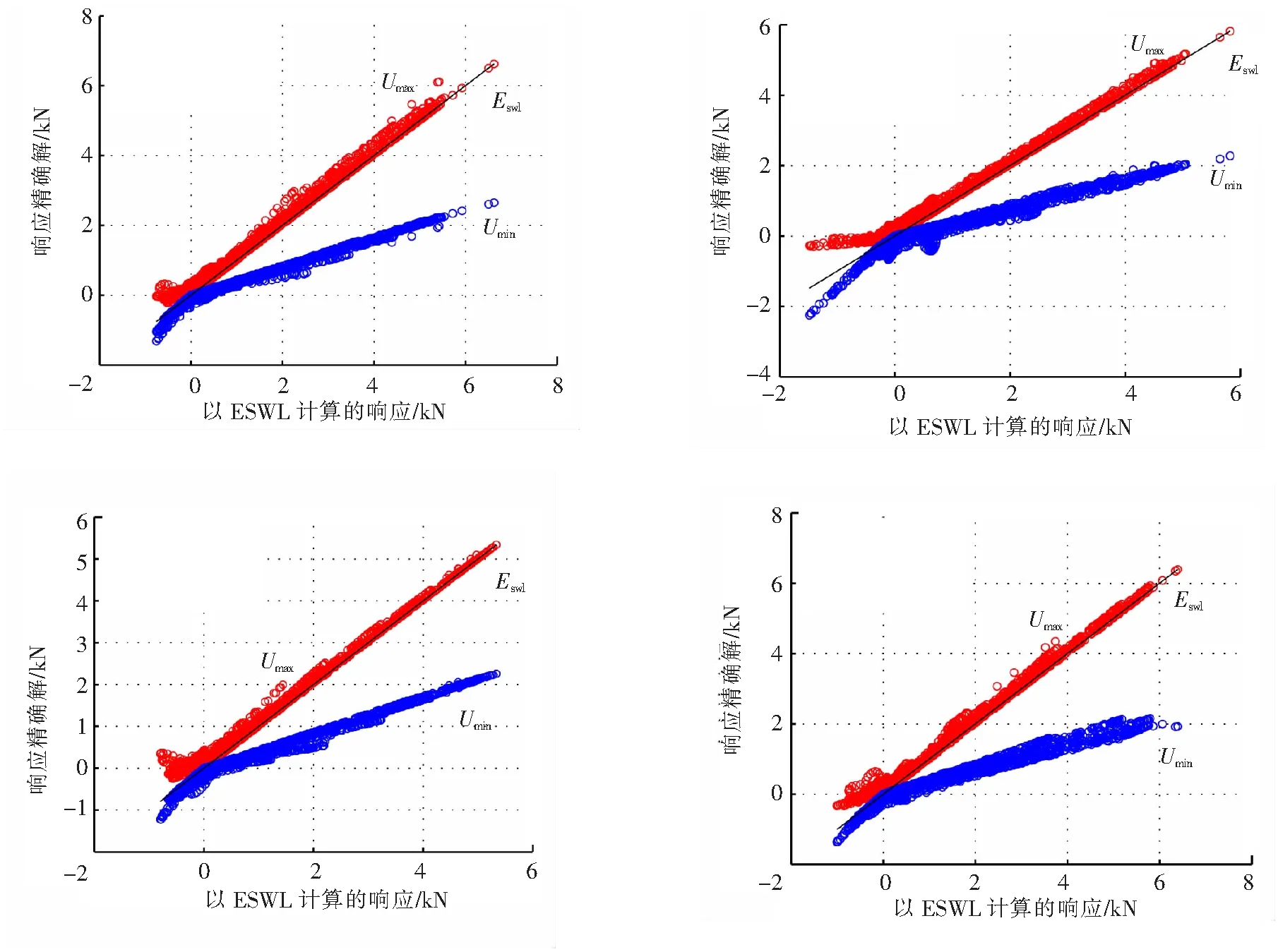
图8 屋盖在不同工况下的杆件内力Fig.8 Internal force of roof links versus wind direction

/

[1] DAVENPORT A G. Gust loading factors[J]. ASCE J Struct Division,1967,93:11-34.

[2] KASPERSKI M, NIEMANN H J. The LRC (Load-response-correlation) method: A general method of estimating unfavourable wind load distributions for linear and nonlinear structural behavior[J]. J Wind Eng Ind Aerodyn,1992,43:1 753-1 763.

[3] HOLMES J D. Equivalent static load distributions for resonant dynamic response of bridges[A]. Proceedings of the 10th International Conference on Wind Engineering[C]. Copenhagen:[s.n.], 1999.907-911.

[4] 谢壮宁,倪振华,石碧青.大跨度屋盖结构的等效静风荷载[J].建筑结构学报, 2007,28(1):113-118.

XIE Zhuangning, NI Zhenhua, SHI Biqing. Equivalent static wind loads on large span roof structures[J]. Journal of Building Structures, 2007,28(1):113-118.

[5] 谢壮宁. 风致复杂结构随机振动分析的一种快速算法——谐波激励法[J]. 应用力学学报, 2007,24(2):263-267.

XIE Zhuangning.New rapid algorithm for wind-induced random vibration of complex structures[J]. Chinese Journal of Applied Mechanics, 2007,24(2):263-267.

[6] 李小康,谢壮宁.大跨度屋盖结构风振响应和等效静风荷载的快速算法和应用[J].土木工程学报,2010,43(7):29-36.

LI Xiaokang, XIE Zhuangning. Efficient algorithm and application for the wind-induced response and equivalent static wind load of large-span roof structures[J]. China Civil Engineering Journal,2010,43(7):29-36.

[7] KATSUMURA A, TAMURA Y, NAKAMURA O. Universal wind load distribution simultaneously reproducing largest load effects in all subject members on large-span cantilevered roof[J].Journal of Wind Engineering and Industrial Aerodynamics, 2007,95:1 145-1 165.

[8] 陈 波,杨庆山,武 岳.大跨空间结构的多目标等效静风荷载分析方法[J].土木工程学报,2010,43(3):62-67.

CHEN Bo,YANG Qingshan, WU Yue. Multi-objective equi-valent static wind loads for large-span structures[J]. China Civil Engineering Journal,2010,43(3):62-67.

[9] 吴 迪,武 岳,张建胜.大跨屋盖结构多目标等效静风荷载分析方法[J].建筑结构学报,2011,32(4):17-23.

WU Di, WU Yue, ZHANG Jiansheng. Multi-objective equi-valent static wind loads for large span roofs[J]. Journal of Building Structures, 2011,32(4):17-23.

[10] HOLMES J D. Effective static load distributions in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002,90(2):91-109.

Wind-induced vibration and equivalent static wind load of roof structures

MA Chao, SHI Biqing

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou Guangdong 510641, China)

The wind-induced response is analyzed by HEM method based on wind tunnel test of rigid building model. Then by using displacement equivalent principle, the equivalent static wind load (ESWL) can be estimated by load response correlation approach. The calculated ESWL and wind-induced response of a gymnasium prove its effectiveness and correctness.

wind tunnel experiment; large span roof; wind-induced response; wind load

1008-1534(2013)04-0233-06

TU312

A

10.7535/hbgykj.2013yx0404

2013-04-07;

2013-05-12

责任编辑：冯 民

马 超(1987-)男，湖北赤壁人，硕士研究生，主要从事结构抗风方面的研究。

E-mail：279158594@qq.com