精密三维坐标法在钢索塔立式匹配测量中的应用

孙景领，黄 腾

（1.南京信息工程大学 遥感学院，江苏 南京 210044；2.河海大学 地球科学与工程学院，江苏 南京 210098）

桥梁结构中的索塔一般是采用混凝土材料或钢材制作完成，但相比较于混凝土索塔而言，钢索塔具有工厂化加工、体积小、自重轻、施工进度快、外形美观、环保等特点，在日本、美国及欧洲各国得到了广泛应用［1］。钢索塔施工阶段一般分为机加工厂房内节段制作加工和桥位现场拼装。钢索塔各节段在工厂机加工完成后，需要对两相邻节段进行立式匹配预拼装（见图1），其目的是为了检验节段间接口的匹配、金属接触率、端面垂直度和塔柱曲线度，同时标定出用于桥位现场拼装的测控特征点和控制轴线，并进行空间坐标测量，所获得的空间坐标和控制轴线是指导桥位现场索塔拼装施工的主要依据［2］。因此，如何获取高精度的三维坐标成为钢索塔立式匹配中的关键工序之一。基于此目的，本文以南京长江三桥钢索塔立式匹配实践为例，对全站仪精密三维坐标法在立式匹配中应用进行探讨，证明此方法的可行性，为类似工程提供借鉴。

1 工程概况

南京长江三桥位于南京长江大桥上游约19km处的大胜关，它是上海至成都国道主干线的重要组成部分。主桥为钢索塔钢箱梁双索面5跨连续斜拉桥，主跨648m，全长1 288m。主塔为国内也是世界上已建桥梁中首次采用外侧线形由倾斜直线段、圆曲线段及竖直直线段组成的“人”字形钢结构索塔，高215m，共设4道横梁，其中下塔柱和下横梁为钢筋混凝土结构，下横梁以上部分全为钢结构。除了钢混结合段外，每个索塔共分为21个节段，每节段长7.7～11.42m，最大吊重不超过160t，节段间采用端面金属接触，M24高强螺栓连接。钢索塔总重约12 000t，其概貌及节段划分如图2所示［3］。

2 专用测量控制网的建立

为了获取钢索塔每节段测控点的三维坐标及节段间相关数据信息，必须先在立式匹配现场建立高精度的专用测量控制网。如图3所示，将需要匹配的钢节段以每两节为单位架设在长、宽、高分别为6.8m、5.0m、0.5m的钢结构胎架上。专用测量控制网是以支撑胎架几何中心为坐标原点，以垂直主轴线为基准。由于胎架中心无法确定，采用多次逐步归化法设置A、B、C、D4个基准点，网形为大地四边形，网的边长约为35m。在4个基准点上现浇注带有强制对中基座的混凝土观测墩，确保对中误差小于±0.05mm，以提高测量精度。按边角网，采用Leica TCA2003（标称精度：测角0.5″，测距1mm＋1ppm）高精度全站仪观测全网的边长和角度。经过严密平差后，求得各点点位中误差均小于±0.35mm。

图3 钢索塔立式匹配专用测量控制网

高程控制网选择胎架顶面为0m基准高程，使用精密水准仪，以二等水准测量技术要求测定各混凝土观测墩对中基座顶面的高程值，各点高程中误差均小于±0.07mm。

3 钢索塔节段测量点布设

在T2～T21每个钢节段靠岸侧壁板上设定特征点4个，其中位于中轴线上2个（U、D），分别距上边缘和下边缘1.0m；壁板左、右角各1个（L、R），分别距上边缘150mm、侧边缘10mm，如图4所示。点位用φ1mm洋冲眼标定，周边贴直径为15mm圆形荧光纸，洋冲眼位于圆形荧光纸中心，便于夜晚测量时搜寻目标。钢节段是个刚性体，桥位现场拼装时，只要测出4个特征点的空间坐标，通过其几何关系及数学转化，即可确定钢节段的空间姿态。因此，立式匹配时4个特征点的三维坐标必须精确测定［4］。

T1是桥位现场架设测控方法的过渡节段［4］，不仅在靠岸侧壁板上设定4个特征点，在靠桥轴线的内侧壁板上同样设定了4个特征点（见图4）。

图4 钢节段测量点布设示意图

4 全站仪精密三维坐标法及精度分析

4.1 测量方法

根据摆放在胎架上钢节段岸侧壁板的朝向，在设置特征点的壁板正面控制点上（A点）架设全站仪，后视另一控制点（D点），以全站仪三维坐标法直接测出特征点的三维坐标，如图5所示。

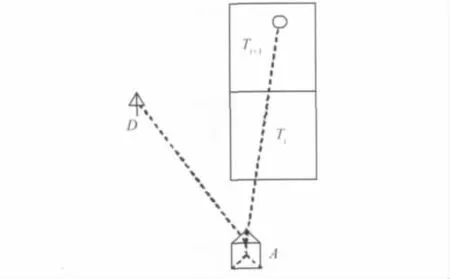
图5 全站仪三维坐标测量法示意图

全站仪精密三维坐标法测得的坐标为［5］

式中：（X0，Y0，Z0）为测站点坐标，S，D分别为测站点和目标点之间的斜距和平距，α，β分别为测站点和目标点之间的竖直角和方位角，i为仪器高，v为棱镜高，K为测站点到目标点的单向大气折光系数，R为地球曲率半径。

由于钢节段特征点上不能安放常规棱镜，因此，采用自制加工的手持棱镜作为照准标志，如图6所示，并在测量前采用比对法测出棱镜常数［6］。测量时，全站仪首先瞄准目标点洋冲眼，再将特制棱镜的“定位点”精确对准洋冲眼，使棱镜面朝向全站仪即可精确测定洋冲眼的三维坐标。

图6 特制手持棱镜示意图

4.2 测量精度分析

4.2.1 平面精度分析

在钢索塔立式匹配测量的各项误差中，由于专用控制网中点位均采用强制对中装置［7－8］，对中误差很小，可忽略不计；各节段的测量特征点在厂房节段加工时均已标定出来，匹配测量时用专用手持棱镜的定位点直接对准作为特征点的洋冲眼，这样标定误差也可以忽略不计。

由式（1）根据误差传播定律可求得点位在X和Y方向上的坐标中误差为

所以，平面点位中误差为

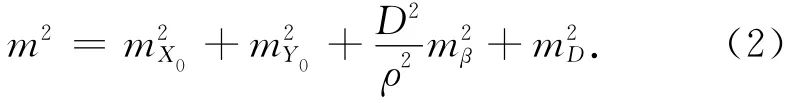
式中：mX0，mY0为控制点误差，mβ为方位角观测中误差，mD为边长观测误差。各项误差对测量点精度影响如下：

1）专用控制网点的影响误差m1不考虑控制点点位在X，Y方向上的互协方差，则其对点位的影响值为

控制网中最大点位中误差不超过0.35mm，因此，取m1＝0.35mm。

2）mβ的影响误差为

其中，D为测站点到测量点的水平距离。根据匹配现场的实际情况及不利因素，取D＝50m，mβ＝0.8″，ρ＝206 265″，则有m2＝0.19mm。

3）mD的影响误差m3一般采用全站仪的标称精度来计算边长测量误差对测量点位的影响，其计算公式为

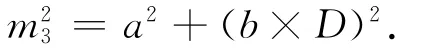
其中距离D＝0.05km，TCA2003全站仪中，a和b的值都为1，则有m3＝1.00mm。

综上分析，测量点的平面点位总误差为

因此，采用全站仪精密三维坐标法能够满足钢索塔立式匹配各节段平面精度的要求。

4.2.2 高程定位精度分析

由式（1）根据误差传播定律可知Z方向上的中误差为

式中：mα为竖直角测量误差，mD为边长观测误差，mk为大气折光系数误差，mi为量仪器高误差，mv为目标量高误差。各项误差对点位高程测量影响如下：

1）竖直角观测对测量点的影响

根据匹配现场的实际情况及最不利因素，取D＝50m，α＝23°，mα＝0.8″，ρ＝206 265″，则有：m4＝0.23mm。

2）距离D的测量误差对测量点的影响

大气折光系数K的取值为0.14，α＝23°，D＝50m，R＝6 370km，1.00mm，则得m5＝0.43mm。

3）仪器高、目标高量取误差用游标卡尺从3个不同方向量取仪器高度，取其误差mi＝±0.2mm；使用专用手持棱镜作为照准目标，因此，目标高mv＝0。

4）大气折光系数误差mk的影响。钢索塔立式匹配测量时间选在凌晨3：00～5：00进行，此时间段内大气温度变化相对比较平缓，大气折光系数较为稳定，而且观测距离也较短，所以不考虑大气折光系数误差mk对高程测量的影响。

综上分析，测量点的高程总误差可按下式计算：

因此，采用全站仪精密三维坐标法也能够满足钢索塔立式匹配各节段高程测量的精度要求。

5 结 论

通过全站仪精密三维坐标法在南京长江第三大桥钢索塔立式匹配测量中的实际应用，并根据匹配区的实际情况及不利观测条件，计算和分析了精密三维坐标法的实测精度，得出以下结论：

1）采用全站仪精密三维坐标法获取钢节段特征点的空间位置信息是可行的，精度满足设计要求，为钢索塔桥位施工现场拼装测量提供了可靠依据，同时也为钢索塔竣工后的最终线形符合设计要求奠定了基础。

2）钢索塔立式匹配测量定位精度要求较高，而且要获得节段间匹配的相关数据。因此，必须建立高精度的专用测量控制网，并采取相关措施以提高控制网的精度。

3）由于钢索塔节段特征点位置上不能安放常规的测量棱镜，所以必须自制专用的即方便使用又能满足测量要求的测量照准标志。

4）从三维坐标法精度分析可知，测距精度对测量结果影响较大，而且其它几项误差也与测距有关，因此，在观测过程中必须采取相关措施以提高测距精度，例如，使用精度较高的TCA2003全站仪，选在凌晨3：00～5：00间大气温度变化相对稳定时段进行观测等。

［1］黄腾，蒋敏卫.钢索塔建造中精密测控技术研究及应用［R］.南京：河海大学，2006.

［2］李宗平，唐启，张六一.南京长江第三大桥钢塔柱安装施工［J］.施工技术，2008，27（5）：105－110.

［3］崔冰，孟凡超，冯良平，等.南京长江第三大桥钢塔柱设计与加工［J］.中国铁道科学，2005，26（3）：42－47.

［4］黄腾，李桂华，陈建华，等.特大型斜拉桥钢塔柱架设精密测控技术［J］.工程勘察，2008（12）：44－48.

［5］胡伍生，潘庆林，黄腾.土木工程施工测量手册［M］.北京：人民交通出版社，2005：139－141.

［6］黄腾，蒋敏卫，李桂华.无基座手持棱镜的设计与使用［J］.测绘通报，2008（7）：61－63.

［7］李广晔，兰雁.强制对中观测墩的制作［J］.地矿测绘，2004（3）：43－44.

［8］姜华根.测量仪器对中方法研究［J］.西南林学院学报，2003（2）：56－60.