基于Monte Carlo采样策略的UKF算法应用

万某峰，赵长胜，王 飞，陈士城

（徐州师范大学 测绘学院，江苏 徐州 221116）

由于近似非线性函数的概率密度分布比近似其函数更容易。因此，UT变换选择一组点集（Sigma点集）来表征输入状态的分布特征，再将非线性变换应用于Sigma点，得到非线性转换后的点集，对转换后的点集通过加权计算得到统计特性。UT变换算法的关键是Sigma点采样策略，由采样策略得到的Sigma点集要能保证输入变量的分布特征，体现非线性函数本身的非线性［1－7］。Monte Carlo模拟方法的基本思想是面对一个问题，首先建立与描述该问题有相似的概率模型，然后对模型进行随机模拟或统计抽样，即产生一组随机数来模拟该随机模型，它的分布与该随机模型相同，再以该随机数的统计特征作为原始问题的近似解［8］。使用Monte Carlo模拟方法生成符合输入状态分布的随机变量，符合UT变换思想。

1 非线性系统的卡尔曼滤波

设某非线性系统模型如下：

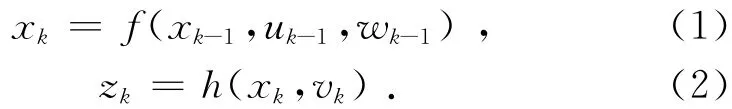
式（1）为状态模型，式（2）为量测模型。式中：xk为k时刻状态向量，uk－1为控制向量，wk－1为模型噪声向量，zk为k时刻的观测向量，vk为量测噪声向量，这里假设wk－1和vk均为高斯白噪声，即均值为0，方差分别为Qk－1和Rk。

假设所有的随机变量均服从高斯分布，非线性卡尔曼滤波公式如下：

预测方程

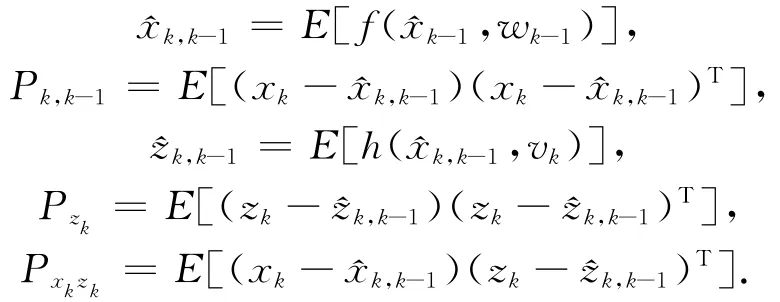
更新方程

2 基于Monte Carlo采样策略的UKF算法

这里考虑wk－1和vk均为加性噪声，并且状态方程为线性，观测方程为非线性，设系统的状态满足高斯分布，系统模型为

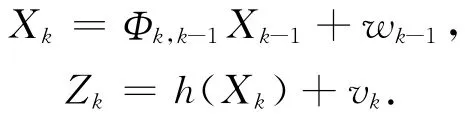
假设wk－1和vk互不相关，且协方差矩阵分别为Qk－1和Rk，n维随机变量X初始状态的均值和方差分别为x0和P0，即随机变量X服从高斯分布。

2.1 Monte Carlo采样策略

Monte Carlo采样策略的关键是产生符合输入状态分布的随机数，随机数产生步骤：

1）确定一个数学模型或某种规则；

2）规定初始值；

3）按一定的步骤产生随机数，重复下去，得到随机数序列。

这里直接调用MATLAB软件带有的高斯分布随机数产生函数—normrnd函数［9－10］

返回m个均值为ave，标准差为sig的高斯分布的随机数A。

采用Monte Carlo采样策略，对均值为x0，方差为P0的n维随机变量X，生成的m个χ（Sigma点集）为

其中：（x0）i表示x0的第i个值，表示P0第i个对角线元素的平方根值。

2.2 UKF算法步骤

1）根据k－1时刻的状态估计值和其协方差Pk，计算状态预测值和协方差Pk，k－1。

2）由和Pk，k－1，采用Monte Carlo采样策略生成Sigma点集

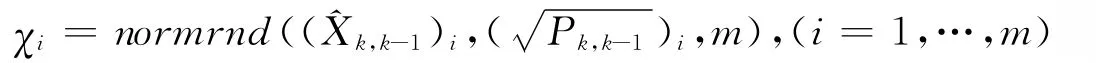
3）通过非线性量测方程传递Sigma点，计算预测值和其协方差Pzk。

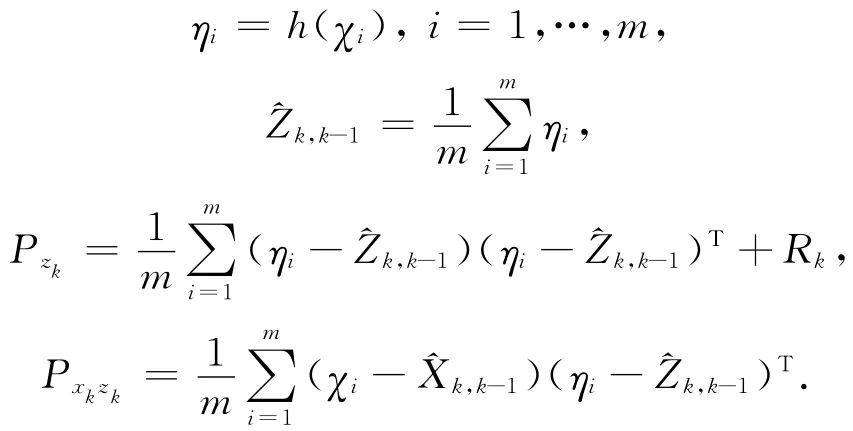
4）计算滤波增益和k时刻状态估值＾Xk，k和其协方差Pk。

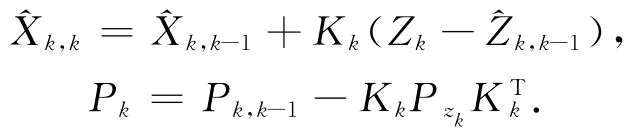
3 仿真实验分析

一个在二维平面内运动的质点M，初始位置（0，3 000），它以初速度Vx＝10m/s，Vy＝50m/s，加速度ax＝2m/s2，ay＝－4m/s2运动，假设一坐标位置为（0，0）雷达对M进行测距rk和测角φk，系统噪声和测量噪声均为加性噪声，状态向量为Xk＝，量测向量为Zk＝［zk1，zk2］T，建立卡尔曼滤波模型

其中：

假设系统噪声wk和vk协方差分别为Qk和Rk，二者不相关。MonteCarlo采样策略生成Sigma点数为5 000，采样时间t＝0.5s，观测次数100次。

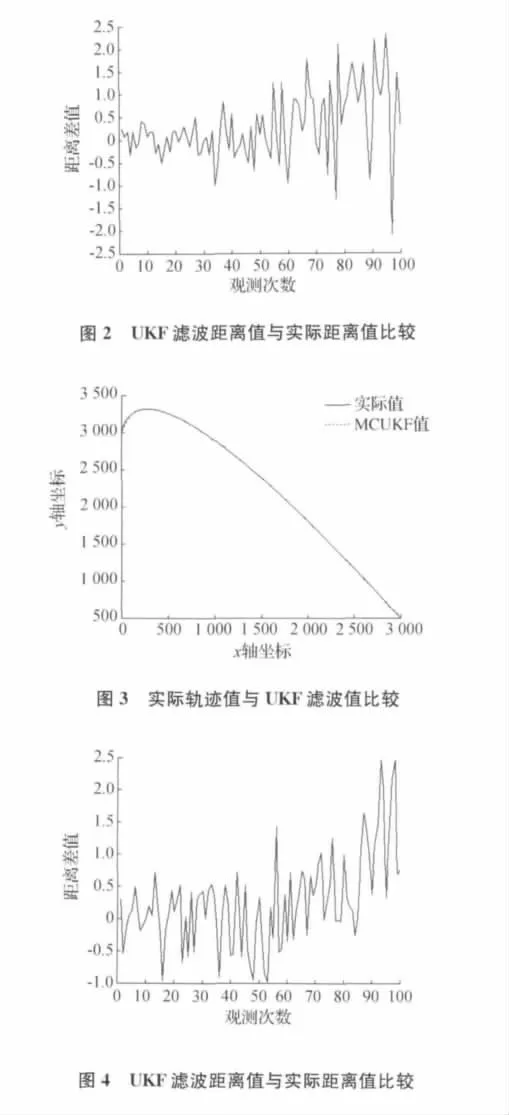
当R＝diag［0.09 0.0012］，Q＝diag［10 10 0.01 0.01 0.0120.012］时，比较结果见图1、图2。

图1 实际轨迹值与UKF滤波值比较

当R＝diag［0.09 0.0012］，Q＝diag［100 100 0.01 0.01 0.0120.012］时，比较结果见图3、图4。

当R＝diag［10 0.0012］，Q＝diag［1 1 0.01 0.01 0.0120.012］时，比 较结果见图5、图6。

当R＝diag［100 0.0012］，Q＝diag［1 1 0.01 0.01 0.0120.012］时，比 较结果见图7、图8。

1）从图1、图3、图5、图7，可以看出，在模型误差和观测误差不是很大时，利用MonteCarlo采样策略的UKF滤波结果均能很好地跟踪目标。

2）比较图2和图4，可以得到，在观测误差较小的情况下，模型误差的大小对UKF滤波结果影响较小，即此时滤波结果精度更依赖观测值精度。

3）比较图6和图8可以得到，在模型误差保持不变的情况下，观测误差对UKF滤波结果影响较大。

4 结束语

MonteCarlo采样策略是一种随机性采样方法，保证了得到的Sigma点集符合输入状态分布特征，再用大量的Sigma点逼近概率密度分布，从而得到更高阶近似，充分体现了非线性函数本身的非线性。采用MonteCarlo采样策略的UKF具有一定的实用性和参考价值，因此，可做进一步应用研究。

［1］王新洲.非线性模型参数估计理论与应用［M］.武汉：武汉大学出版社，2002.

［2］JULIER S J，UHLMANN J K，DURRANT－WHYTE H F.A New Approach for Filtering Nonlinear System［C］//Proceeding of the American Control Conference.USA：IEEE，1995：1628－1632.

［3］JULIER S J，UHLMANN J K，DURRANT－WHYTE H F.A New Method for the Nonlinear Tranformation of Means and Covariances in Filters and Estimators［J］.IEEE Trans，Automatic Control，2000，45（3）：477－482.

［4］JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［J］.Proceeding of the IEEE，2004，92（3）：401－422.

［5］JULIER S J.The spherical simplex unscented transformation［C］//Proceeding of the American Control Conference.USA：IEEE，2003：2430－2434.

［6］程水英.无叶变换与无叶卡尔曼滤波［J］.计算机工程与应用，2008，44（24）：25－35.

［7］刘也，余安喜，朱炬波，等.加性噪声条件下的UKF算法［J］.中国科学，2010，40（11）：1286－1299.

［8］王中宇，刘智敏，夏新涛，等.测量误差与不确定度评定［M］.北京：科学出版社，2008.

［9］邓薇.MATLAB函数速查手册［M］.北京：人民邮电出版社，2010.

［10］李海涛，邓樱.MATLAB程序设计教程［M］.北京：高等教育出版社，2010.