基于总体最小二乘的相似变换模型及其在地图扫描数字化中的应用
2013-12-06岳东杰
袁 豹,岳东杰,张 亮,王 露
(河海大学 测绘科学与工程系,江苏 南京 210098)
在信息化时代的今天,对于空间数据的获取、编辑、分析和应用的方法已有很多,其中地理信息系统(Geographic Information System,GIS)是一门发展迅速、应用广泛的地理空间数据分析技术。在建立GIS的过程中,地图数字化是一种重要的数据来源。地图数字化(MapDigitizing)是指利用地图图形或是图像信息的模拟量将其转换为离散的数字量,从而应用到数据处理软件中进行分析。数字化方式有手扶跟踪数字化和扫描数字化两种常用方式,而随着技术的发展和精度要求的提高,现在大多采用扫描数字化的方法。扫描数字化有着操作速度快、自动化程度高的优点。
通过地图扫描数字化方法获得的最终数字成果,其精度受到原始地图、扫描操作、矢量化过程和数据处理等方面的综合影响。近些年,对于地图扫描数字化的精度分析研究逐渐增多,郝向阳、钱曾波对扫描数字化的点位精度进行了分析,发展了定向点和采样点的自动对中算法[1];余晓红分析了扫描数字化误差的特点和来源,提出扫描数字化误差不一定服从正态分布,并且更多地表现出系统性[2];童小华、周德意讨论了地形图扫描纠正的精度问题[3];毛泽卫针对地图扫描数字化中的各种变形,讨论了不同处理方法和精度比较[4]。在地图扫描数字化处理过程中,有一项重要的工作是图纸定向。图纸定向即是利用一定数量的控制点通过建立数学转换模型将图像坐标转换为实际的地理坐标,确定好定向参数后,即可实现图内所有采样点的转换。较为常用的模型有相似变换模型、多项式模型和仿射变换模型等,本文着重讨论相似变换模型。图纸定向这一环节的误差大小对后续数字化成果的质量有着重要影响。本文认为定向点的采集存在不可忽略的误差,提出总体最小二乘(Total Least-squares,TLS)方法,同时顾及定向点采集误差和地理坐标的测量误差,建立基于总体最小二乘方法的相似变换模型,结合实验分析,得到相关结论。
1 相似变换模型
相似变换定向模型可以表示为

其中:(X,Y)为地理坐标系坐标;(x,y)为地图图像坐标系坐标;a0,b0,a,b为定向参数。写成矩阵形式为

根据最小二乘原理可得定向参数的估计值为
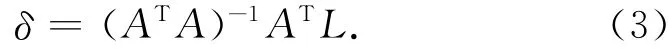
图纸定向的精度可用定向点坐标改正数计算如下:

2 基于总体最小二乘的相似变换模型
2.1 总体最小二乘基本原理
在线性方程组AX=L中,总体最小二乘[5]的基本思想就是同时考虑L和A的扰动。基于总体最小二乘的相似变换模型可归结为
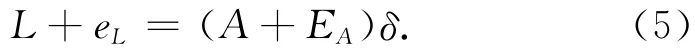
且有

其中:QL和QA分别为eL和eA的对称非负定协因素阵,其中eA=vec(EA),EA为系数矩阵的误差,eL为观测值阵的误差,误差矩阵[EAeL]属于相互独立的白噪声误差且这里认为误差精度相同,则有QL=I,QA=I。
2.2 模型求解及精度评定
总体最小二乘的准则可以表示为

对于总体最小二乘问题的解法,主要有奇异值分解(SVD)法和迭代解法,此处采用SVD方法解算定向参数的估计值。因为系数矩阵A中第一列和第二列是固定列,不含有误差(即不需要改正),所以此处采用混合总体最小二乘的解算方法。
令A=[A1A2],其中,构造C=[AL],并对其作QR分解得到

其中:Q为正交阵,R为上三角阵。则有

令CR=[R(n-2)×2R(n-2)×1],并对其进行奇异值分解得到

其中,∑为奇异值矩阵,取其中最小奇异值并表示为σn2+1,则参数估计值为

其中n2为系数矩阵A中非固定列对应的参数个数,此处n2=2。
增广矩阵CR的改正数为
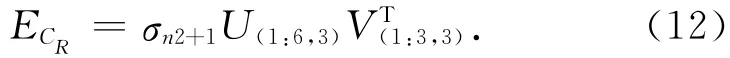
则R的改正矩阵为

由此可以计算出系数矩阵和观测矩阵的改正数为

根据定向点坐标改正数,得出总体最小二乘法的精度评定方法为

3 应用及实验分析
在平面坐标转换中也经常采用相似变换模型,基于总体最小二乘方法的相似变换模型,理论上较为严密。应该在地图扫描数字化图纸定向的其他模型引入总体最小二乘这种严密的平差方法。本文依托长江水下地形图数字化二期项目,对长江流域南京河段1∶2 000水下地形图进行数字化处理,建立水下地形GIS数据库,便于对水下地形数据的编辑、管理和更新。为了验证基于总体最小二乘的相似变换模型的定向效果,本文针对Arcgis软件中地形图数字化的图纸定向问题,进行了计算和分析。图幅西南角如图1所示。
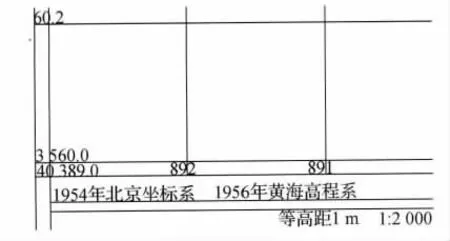
图1 图幅西南角
实验方案:分别采用4定向点、6定向点和8定向点进行定向参数的求解,其中4定向点取图幅4个图廓点,6定向点取图幅4个图廓点和左右图廓点连线的中心点,8定向点取图幅4个图廓点以及图廓点连线的4个中点。采用最小二乘和总体最小二乘两种方法求解参数,如表1所示。
从表1可以看出,从定向参数来看,最小二乘法与总体最小二乘法有一定差别,不同定向点得到的定向参数不同。为比较最小二乘法与总体最小二乘法的定向效果,计算出模型的定向精度如表2所示。

表1 定向参数结果
从表2可以看出,基于总体最小二乘方法的相似变换模型具有较高的定向精度,定向点的个数影响定向精度,在实际地图扫描数字化中应该采用总体最小二乘方法,选择合适的定向点个数。

表2 最小二乘法和总体最小二乘法的定向精度比较mm
4 结 论
1)相似变换模型在地图扫描数字化中应用较多,针对该方法在图纸定向中应用的精度问题值得深入研究。
2)基于总体最小二乘方法的相似变换模型可以获得较高的图纸定向精度,优于最小二乘方法。
3)在地图扫描数字化中,在采用其他定向转换方法时也应该采用总体最小二乘方法。
4)关于定向点数量的选取以及定向点位置的不同对数字化精度的影响,结合扫描数字化中其它环节的误差,综合考虑地图扫描数字化的精度问题需要进一步研究。
[1]郝向阳,钱曾波.地图扫描数字化的点位精度分析[J].测绘学报,1996,25(1):46-52.
[2]余晓红.地图扫描数字化的误差分析[J].测绘科学,2001,26(4):49-52.
[3]童小华,周德意.地形(籍)图扫描纠正的精度分析[J].同济大学学报,2003,31(1):77-81.
[4]毛泽卫.基于MAPGIS的地形图变形处理方法比较[J].测绘与空间地理信息,2009,32(6):162-168.
[5]GOLUB G H,VAN LOAN C F.An Analysis of the Total Least Squares problem[J].SIAMJ Numer Anal.1980,17(6):883-893.
