基于遗传算法的PID控制器参数优化研究

2013-12-06谭顺学

大众科技 2013年5期

谭顺学

(柳州职业技术学院，广西柳州 545006)

1 前言

PID控制器广泛应用于工业控制领域，PID控制器在实际应用过程中，如何设定PID控制器的控制参数，是PID实际应用过程中面临的一大难题，目前针对PID控制器参数整定的研究方法有很多，既有基于实践经验的参数设定方法，也有基于逻辑推理和一些人工智能，如神经网络理论等展开的相关研究、基于遗传算法，通过模拟进化论的思想在通过不断地一代接一代的遗传采取优胜劣汰的优化原则，最终对这类解空间不确定的问题，寻找到最似最优解应用于遗传算法[1-4]。

对PID参数整定的相关研究主要有：牛芗洁，王玉洁，唐剑等人为了解决PID控制器参数优化的问题，提高PID参数优化精度，提出一种遗传算法的PID参数优化策略。优化过程中通过对PID控制器参数建模，将PID参数作为遗传算法中的个体，采用控制误差绝对值时间积分函数作为优化目标，实现了对PID的三个控制参数的动态调整[5]。曹建秋，徐凯针对变风量空调系统的不确定性和参数整定的需求，提出了一种基于遗传算法的PID参数优化方法，在优化过程中采用模糊控制和变论域模糊的新方法，分别用于提高PID参数动态调整的性能和对阶跃信号的稳态调整性能，有效提高了PID参数优化的精度和稳定性[6]。郭旭红，芮延年，李军涛等人提出基于模糊子系统和遗传算法子系统的PID参数调整系统,并利用Matlab软件对基于遗传算法模糊智能空调系统进行了仿真，设计过程中以舒适度为目标函数,通过遗传算法实现了PID参数的最优化调整[7]。

然而，在直接应用于遗传算法对PID参数整定过程中，经过实践检验存在两大问题，其一是计算复杂度较高，为了寻找到最优解，往往需要尽可能的让种群具备的多样性，扩大种群的个体数目，种群的规模越大，进行一轮遗传算法复杂度越高，而且，为了找到遗传最优解，遗传算法的代数一般设的比较大，以得到更多可能接近最优解的个体。另一方面遗传算法本身就有一些难以解释的现象，以生物学的进化论为例，生物的进化并不是沿着一个线性均匀的规律进行种群的演化[8－9]。而且，近年大量研究表明，物种的进化实际是在种群产生的初期进化初期进化最快，中后期比较慢，而且在进化过程中不同的基因发生遗传和变异的几率不一样，对物种表征最重要的一些基因，这些基因在遗传过程中，在遗传过程中发生的变异的概率极低。而一些对物种表征不明显的基因，则更容易发生变异，种种这些规律，用传统的遗传算法是不能够模拟的，因此，用模拟遗传算法解决各种现实问题求解的过程中，也必须对遗传算法进行一定的改定，使得遗传算法能够更好地模拟真实的遗传过程，加快在一个庞大的解空间中，寻找到近似最优解的速度，而且应该尽可能的避免近似最优解陷入局部最优解的局限[10－11]。为此，文章设计使用遗传算法的PID参数整定并反而催参数针对过程中的特点对遗传算法的改进和优化。

2 基于遗传算法的PID参数整定

使用遗传算法对PID参数进行整定的原理图，如图1所示，从图1可以看出，在对PID参数进行整定时，首先，需要对PID控制器以及PID控制器的控制对象，进行建模，建立PID控制器输入和输出之间的模型关系。然后，根据对PID控制器设定的输入量，也即进行PID控制时的控制预期量，输入量输入PID控制器之后，对目标系统进行实际的控制，根据实际的控制结果进行采样，得到通过PID控制器对目标系统的实际控制效果。采样值与预期设定的初始输入量之间进行对比，之间的差值就是PID控制器的控制误差[12]。一个理想的PID控制器应该尽可能建立控制误差，而且，理想的PID控制器还应该具备很强的对节约信号的响应能力，即当PID控制器在实际控制过程中，如果目标系统受到外部的一些干扰信号，或者造成信号的影响，对目标系统的实际控制结果应该和预期的设定值基本一致。目标系统在可控的范围内，无论受到哪一种类型的干扰，系统都能够保证稳定的运行。PID控制器为了实现这一效果，需要动态的对PID控制器的控制参数进行调整[13]。对PID控制参数的调整则是本文的研究重点。如图1所示，运用遗传算法对PID控制器的输入量和实际控制过程中产生的误差进行分析，经过遗传算法进行若干代的遗传计算，求解到PID控制器当前最优的参数设置，并实现对PID控制器的参数设定，从而实现整个PID控制器稳定的运行。

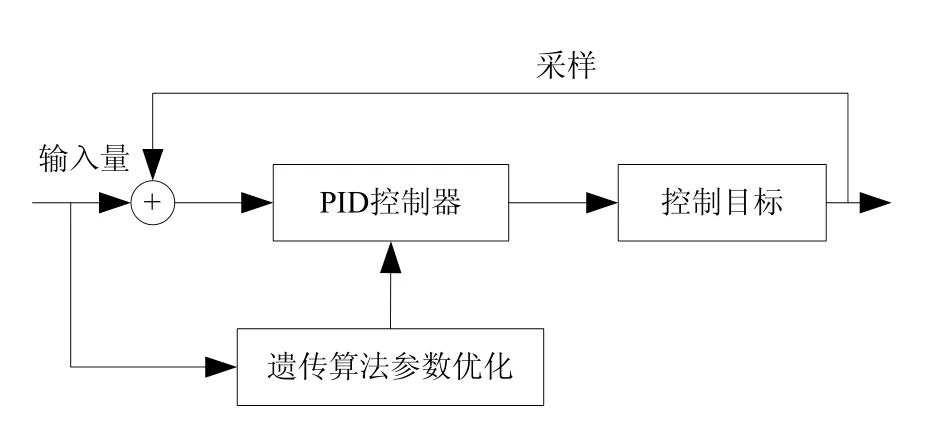
图1 基于遗传算法的PID参数整定原理

根据对PID控制器的工作原理分析，PID控制器的内部有三个控制器所组成，分别是比例控制器、积分控制器和微分控制器，因此，结合在一起，可以形成灵活多样的控制效果，由此，也可得到PID控制器的模型可以用式1表示。

PID控制的模型：

目标函数：

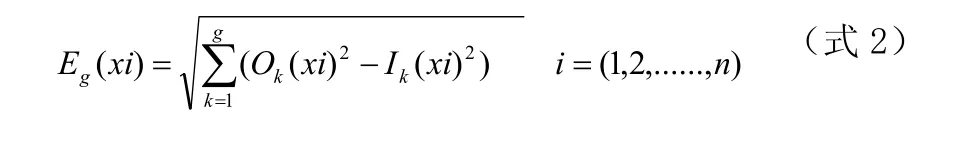
式2中g表示遗传算法已经经历过的遗传代数，k为记录从开始遗传到当前位置的代数，表示在第k代遗传时，作用在被控对象的实际输出值，表示在第k代遗传时，作用在被控对象的输入预期值。

适应度函数：

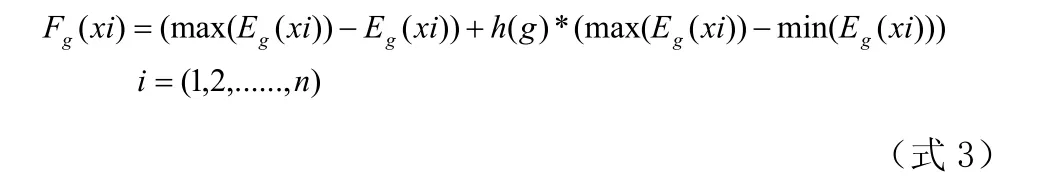
式 3中h(g)为在第k代遗传时的历史累计偏差调节因子，该因子是随着遗传代数的变化动态调整，调整为式4：

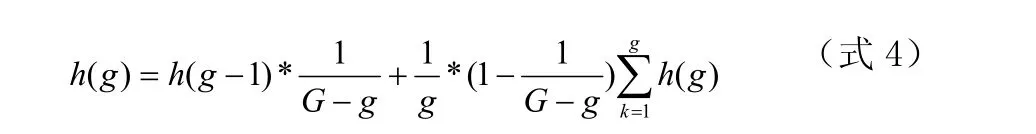
式中G总的遗传代数，g表示遗传算法已经经历过的遗传代数，h(g-1)代表上一代的遗传算法使用的累计偏差调节因子。该式表明了历史累计偏差在遗传早期起较重要的作用，在遗传后期的作用权重逐步降低。

利用遗传算法对PID控制器参数整定的过程如下。

（1）初始种群的确定。初始种群的确定是遗传算法开展运算的前提和基础，为了使得遗传算法能够更快的求解得到近似最优解，初始种群应该尽可能取接近于最优解的可能情况。当然，在实际的工程应用过程中，由用户直接去设定接近最优解的情况并不是太容易，但是一般可以根据工程经验设定目标系统的可能最优解。另一方面，初始种群的个体、数目直接影响着遗传算法的计算性能。如果初始种群的数目过少，则遗传算法可能在短时间内陷入局部最优解的情况。如果初始种群的个数过于庞大，则遗传算法的计算复杂度过高。计算过程中需要耗费大量的时间。文章在设计基于遗传算法的P参数整定过程中，初始种群根据工程经验对三个参数分别选取了三个可能的近似最优解。然后，在这三个参数的基础上，进行±5%、±10%和±15%的变形。通过这种变形之后，每个参数就形成了七个可能的取值，对三个参数所有七种可能取值进行排列组合，共形成343种可能的排列，这343种排列，即形成遗传算法的初始种群。

（2）个体评价。建立初始种群之后，根据式3所示的适应度行数，对初始种群中的每个个体计算其适应度的值。其适应度值作为个体评价的依据。适应度值越高，则认为该个体在整个种群中更占优势，属于更优秀的品种。适应度值较低的个体，则被淘汰的可能性越高。

（3）选择函数。遗传算法计算的关键过程是，遗传是从当前一代的个体遗传到下一代，而在遗传过程中，究竟哪些个体应该被选择作为遗传的父节点，则依靠选择函数来确定。选择函数遗传公式如式5所示，从式5可以看出，在确定选择函数时，实际上是根据每个个体的适应度值确定其被选取的概率，适应度值越高，则被选取的概率也越高，这也验证了刚才所描述的，适应度值表明的是该个体在整个群体中属于较优良的品种，更应该被选取出来作为父节点遗传至下一代。

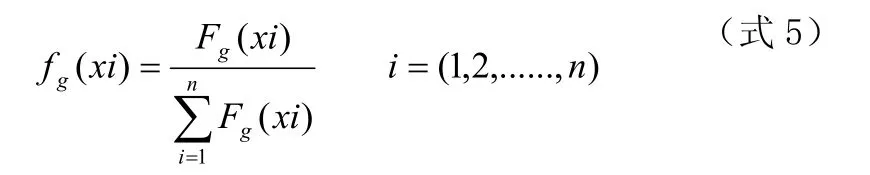
式中n表示当前遗传过程中存在的总个体数目。

（4）交叉算子。交叉算子在遗传过程中对种群中任意二个个体之间的部分编码值进行交叉，以形成新的个体。交叉算子是衡量遗传算法中进行个体编码交叉变化的程度。文章设计的PID遗传算法所选取的对交叉算子采用固定的数值进行设定。进行遗传计算时，任意被选中的二个个体中间选取1～4个比特进行交叉互换。

（5）变异算子。变异算子是遗传算法进行计算时对单个个体内的编码值进行变异的程度。文章所设计的遗传算法实现过程中，变异算法同样采用的固定参数的变异。每个个体的编码进行变异是选取1～4个比特进行变异。

（6）结束条件。遗传算法在运行过程中将根据预先设定的选取函数和交叉变异算子不断地进行一代接一代的遗传，在遗传过程中，可能会得到接近最优解的近似解。此时，为了避免遗传计算无止境的遗传下去，需要设定结束条件。文章设定的接受条件有两个，分别满足：在执行过程中分别满足式6或式7即可结束遗传算法的计算。其中式6表达的是在遗传计算过程中，如果有连续三代的遗传得到的个体，任何产生的一个新一代的个体都不如其原来父节点个体的适应度值。这种现象表明在遗传过程中种群个体并不是朝更优秀的品种发展，而是朝着更差的品种发展。出现这种情况则表明，很可能是出于父节点这一代的种群个体都已经比较优秀了，再进行变异或者遗传操作都可能会导致种群个体的品质下降。

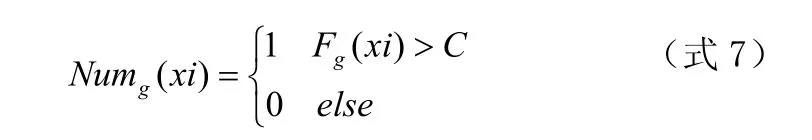
式7所表示的含义是，根据用户预先设定的一个常数C，如果产生的种群个体中适应度值大于C的数目连续三代都不再增加，则此时遗传算法可以结束。

3 遗传算法的算子优化

传统的PID遗传算法在实现过程中，可能存在计算复杂度较高求解近似最优解耗时过长的问题，为此文章对所设计遗传算法进行了优化，优化的方法具体有三个，分别如下：

（1）交叉算子优化。本文设计的遗传算法中，交叉算子是设定是固定1～4比特进行交叉，这种固定比特的交叉在遗传过程中缺乏灵活性。有的时候会出现，个体比特交叉数目过多，通过遗传之后产生过多的新个体，不利于遗传算法的收敛，而有的时候当个体的差异变得非常小的时候，又呈现出交叉的程度不够，通过遗传产生的新个体很可能是以前是出现过的个体，此时，很容易使得求解过程陷入局部最优解的困境，为此，本文设计的交叉算子采用自适应的方式进行动态调整，交叉算子的计算公式如式8所示，公式8描述的是在遗传算法计算过程中每次遗传过程其所选取的交叉算子和上一代所选取的交叉算子的关系，其总体设计思路是交叉算子必须动态的根据种群个体的变化情况和以及当前个体适应度值来动态设定，如果种群个体在遗传过程中，增长的速度过快，即当代种群个体数量大大超过种群上一代个体数量时，则此时对当前这代的遗传算子应该适当选小一些，如果，对种群适应度值较高的个体适应较高的个体具备更优良的品质，这种品质应该尽可能多的遗传到下一代、因此此时所选举的交叉算子应该适当取小一些。

（2）变异算子优化。变异算子在遗传过程中为新的个体发挥十分重要的作用，为了能够使得遗传计算过程时，能够更为灵活的产生的新的个体，对变异算子也才才用了自适应的方式进行设定，设定的原则与交叉算子的设定原则基本一样，因此设定变异算子如式9所示，与式8有较强的相似性。

（3）最优结果的保存。在遗传过程中会不断的产生新的个体，其中某些处于中间代数的种群个体中可能存在最接近最优解的个体，对这些个体，如果不加以保护，通过后续的遗传、交叉和变异等操作可能会使得这些个体又逐渐远离最优解，最终用户无法得到最优解的过程，因此在计算过程中，对于每一代遗传过程，选取适应度值最高的个体直接保留至下一代，同时为了限制种群数目无限制的扩张，在遗传过程中将每一代都将适应度值最低的个体直接进行淘汰，通过这种方式既可以控制种群个体的规模，同时保证遗传过程中所产生的每一代的最优解能够得到保留。

（4）交叉算子

式中nk表示在第k代遗传过程中群体中总的个体数，nk-1表示在第k-1代遗传过程中群体中总的个体数， PJk-1表示在第k-1代遗传过程中交叉算子的数值，α和β分别为交叉算子内的控制因子。

（5）变异算子

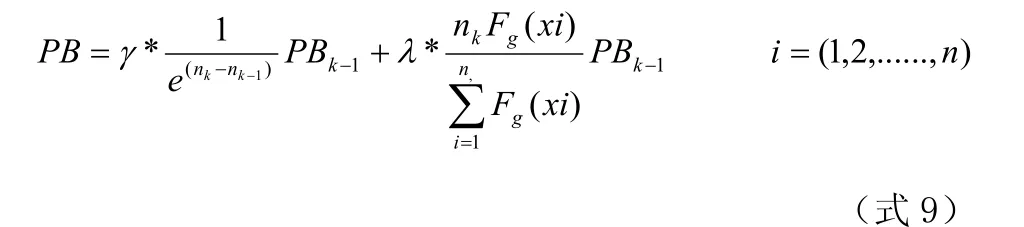
式中 PBk-1表示在第k-1代遗传过程中变异算子的数值，γ和λ分别为交叉算子内的控制因子，其余各参数同前。

4 仿真与测试

文章设计的遗传算法的实际工作性能，分别用传统的遗传算法实现了PID参数的诊定以及应用改进之后PID遗传算法的诊定，测试的结果如图2所示，从图中可以看出，应用改进之后遗传算法对阶跃信号的稳定性更强，在同样的系统输入和干扰的情况下，改进之后的遗传算法对系统中出现的阶跃信号越更强的承受能力和系统的稳定性也更好

同时，文章设计的改进之后的遗传算法在计算过程中能动态调整种群的数目，因此，可以避免遗传算法过早地陷入局部最优解的情况，同时也能加快最优解的搜索速度，对PID控制器参数诊定最优解的求解，对给定精度几乎相当的最优解参数分别用传统的遗传算法和改进之后的遗传算法进行参数诊定，经过测试发现，经过改进之后遗传算法消耗的时间比传统的遗传算法缩短了 14%，由此可见，改进之后的遗传算法，在得到同样精度的最优解的情况下，对最优解的搜索速度提高比较明显。

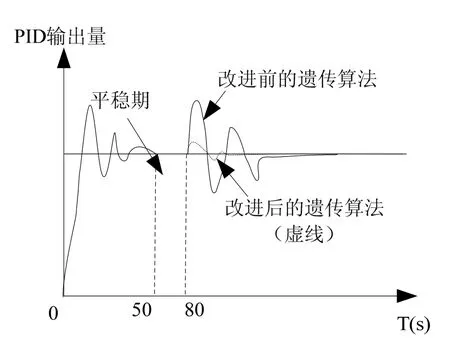
图2 改进前后遗传算法的阶跃信号响应图

5 总结

遗传算法利用生物学的原理解决最优解空间的求解，通过实践检验是一种比较理想的求解方式，而且遗传算法这种求解过程是一种全局的随机搜索方法对最优解求解问题的适应能力较强，因此十分适合对PID参数的整定，本文通过对遗传算法的设计及优化，实现了对PID参数的最优解的快速求解，而且实验结果也验证了了改进之后的遗传算法，具备了更优的性能。

[1] 李红利,张晓彤,兰立柱,孙兆林. 基于遗传算法的RBF神经网络的优化设计方法[J].计算机仿真,2003,20(11):67-69.

[2] 李瑞霞,李粉霞.基于改进遗传算法的PID参数整定策略[J].机械工程与自动化,2008,(06):155-157.

[3] 武交峰,杜永贵.基于自适应在线遗传算 PID 控制[J]. 机械工程与自动化.2006,(06):115-116.

[4] 刘宏波.基于自适应伪并行遗传算法的 PID参数整定[J].化工自动化及仪表,2008,35(03):31-33.

[5] 牛芗洁,王玉洁,唐剑.基于遗传算法的PID控制器参数优化研究[J].计算机仿真,2010,27(11):180-82.

[6] 曹建秋,徐凯.遗传算法优化的模糊+变论域自适应模糊PID复合控制策略[J].信息与控制,2011,40(01):44-49.

[7] 郭旭红,芮延年,李军涛.基于遗传算法的模糊智能变频空调仿真系统的研究[J].系统仿真学报,2005,17(05):1237-1240.

[8] 李坤,李军华,杨小芹.遗传参数协同进化的自适应遗传算法[J].计算机仿真,2007,27(11):204-208.

[9] 史振兴.基于遗传算法的 PID控制器参数优化与仿真[J].仪器仪表与分析监测,2010,(03):4-7.

[10] 丁寅磊,吕丽霞.基于遗传算法的 PID控制器参数优化研究[J].仪器仪表用户,2009,16(01):1-2.

[11] 占自才.基于遗传算法的PID智能控制器设计[J]. 华东交通大学学报,2009,26(01):58-61.

[12] 李玉娜.基于遗传算法的锅炉水温 PID 控制寻优[J].工业控制计算机,2010,23(09):56-60.