基于小波分析的托卡马克真空室环形封闭壳体缺陷无损评价
2013-12-04陈玲莉陈振茂彭海强梁佳宇
陈玲莉,陈振茂,彭海强,梁佳宇
(西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室,西安 710049)
近十几年来,基于结构动态响应特性的无损检测方法已经成为工程结构损伤检测领域的研究热点,同时基于结构全局振动信号的小波分析方法在损伤检测中也愈来愈受到关注。对于梁、桁架及建筑结构等的损伤检测[1-3]已证实小波分析方法在损伤检测方面的实用性和有效性。小波变换是一种时间-尺度信号分析方法,同时又是一种时间-频率分析方法,具有优良的特性,被誉为信号分析的显微镜。在结构振动状态监测中,信号波形发生突变点往往包含结构状态的重要信息,因此结构动态信号突变点的监测与分析对损伤检测具有重要意义。然而对于工程中常用的一类封闭壳体结构,特别是环形旋转封闭壳体结构(如托卡马克真空室),基于动态响应信号、利用小波分析方法进行缺陷的无损评价目前未见研究报道。
笔者主要基于结构损伤前后的动态应变能变化率信号,通过Sym4、DB4、Mexh、Haar四种小波函数连续变换对该类结构进行损伤定位定量识别。因为结构发生损伤将导致小波变换系数极值点改变,所以可以通过结构损伤前后信号的小波变换系数极值变化确定结构具体损伤位置和损伤程度。
1 小波分析托卡马克真空室封闭壳体损伤识别
1.1 损伤结构的有限元模型
托卡马克真空室是国际热核聚变堆(ITER)中主要部件之一,它是一个封闭环形、横截面为“D”形的双层不锈钢高真空壳体结构,双层壳体之间安装大量的用于屏蔽中子流和防止辐射的屏蔽单元,并有大量支持双层壳体结构的加筋肋板和支持内部包块的导管等。
以托卡马克真空室单层封闭环形壳体(图1)为研究对象,设壳体厚度h=0.06 m,弹性模量E=2.07×1011Pa,密度ρ=7.83×103kg·m-3,泊松比μ=0.282。通过ANSYS进行瞬态电磁力作用下的结构动态响应数值的模拟,单元类型shell63,共划分3 040个单元。因为封闭壳中部环向支撑在TF(Toroidal Field,环向线圈)线圈上,模拟计算中将中部环向所有节点设定为固定约束。并利用刚度下降法(即弹性模量下降百分比)来模拟结构多处单元不同损伤程度。假定结构在单处或者多处损伤是沿壳体厚度均匀分布,可利用弹性模量下降模拟单元损伤[5-7],即:
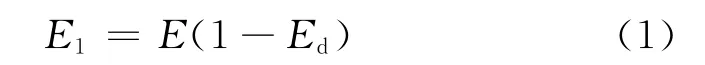
式中:E为无损伤时单元弹性模量;Ed为单元局部损伤程度(弹性模量下降百分比);E1为损伤后的单元弹性模量。
单层封闭壳体完好和多处损伤有限元模型如图1所示。假设三种损伤工况如下:
(1)单处损伤:1 502号单元50%损伤;(2)两处损伤:1 502号单元50%损伤,1 290号单元20%损伤;(3)三处损伤:1 502号单元50%损伤,1 290号单元20%损伤,1 684号单元80%损伤。

图1 托卡马克真空室封闭单层壳体损伤有限元模型
1.2 动态应变能信号提取
根据参考文献[7],笔者把动态应变能变化率ΔE作为小波分析信号,其定义为式(2)~(4)。
损伤前动态应变能:

损伤后动态应变能:
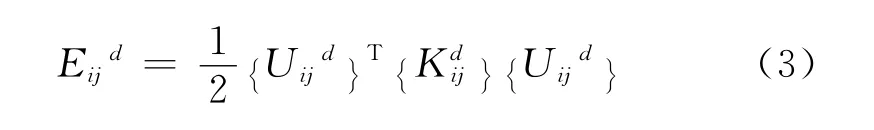
动态应变能变化率:

式中:Eij和分别为结构损伤前后第j个单元在i时刻的动态应变能;Kij和分别为结构损伤前后第j个单元在i时刻的刚度;Uij和分别为损伤前后第j个单元在i时刻的动态位移;T 表示向量或矩阵的转置。
1.3 小波分析结构多处缺陷无损评价
在等离子体线性大破裂时托卡马克真空室内壁会受到复杂的瞬态电磁力作用,参考文献[8]提供的电磁力变化如图2所示。数值模拟在电磁力作用下真空室内壳体结构瞬态响应,提取真空室内层封闭壳体结构损伤前后的单元动态应变能变化率作为小波分析输入信号,分别选择Sym4、DB4、Mexh、Haar四种小波基函数在不同尺度因子(1,20,50,100)下进行多损伤评价研究。

图2 真空室电磁力随时间变化情况
由于篇幅限制,笔者仅给出Sym4小波变换部分检测图,如图3,4所示。图中纵轴小波变换系数峰值表示结构的损伤程度,横坐标表示损伤单元的位置。
1.4 四种小波函数在不同尺度因子下分析精度对比
表1给出四种小波函数在不同尺度因子(1,20,50,100)下的不同损伤工况定量分析精度对比,其中“精度”是指单元刚度下降值(例如:单元损伤50%对应表中的数据是0.5,80%对应的是0.8。通过表1精度分析对比可见:


表1 不同尺度因子、函数下1 502号单元损伤50%(0.5)和1 684号单元损伤80%(0.8)的分析精度对比
(1)四种小波函数对结构多处损伤位置和损伤程度都有着良好的识别效果。
(2)对于损伤程度,四种小波函数均在尺度因子为20时分析精度为最好。
(3)因为Sym4小波函数是Db4小波函数的改进,所以可以看出,这两种小波函数连续小波变换的精度基本一致,实际应用时可任选其一。
(4)对于多处损伤定量识别,随着尺度因子增大,小波分析可能会“湮没”一些真实的较小损伤位置;对于Sym4来说,在尺度因子为20的识别精度比Haar和Db4小波精度好;而Mexh小波函数在小尺度因子下的识别精度要比Sym4、Haar和Db4小波函数识别精度要好得多。
2 结语
笔者基于托卡马克封闭环形封闭壳体结构简化模型,通过瞬态电磁力作用下动态响应数值模拟,提取结构损伤前后的动态应变能变化率作为小波分析信号,利用四种常用小波变换函数,对结构单处、两处、三处损伤工况进行了详细数值模拟研究,得到了良好的损伤识别效果,通过精度评价对比,证明四种小波函数分析对环形封闭壳体结构多损伤定位定量识别方法的实用和有效性。另外在实用中不仅要选择合适的小波基函数,同时最关键的是确定合适的尺度因子(不能太大或太小),要通过多次分析计算才能得到精度较高的定量识别结果。
[1] 任宜春,林琳,马石成.基于小波分析的梁损伤识别方法初探[J].建筑技术开发,2004,31(2):8-9.
[2] 吴浩中,戴小文,王开文.小波变换在摆式列车倾摆控制系统故障诊断中的应用研究[J].机械强度,2003,25(1):12-15.
[3] DOUKA E,LOUTRIDIS S,TROCHIDIS A.Crack identification in beams using wavelet analysis[J].International Journal of Solids and Structures,2003,40:3557-3569.
[4] LOUTRIDIS S,DOUKA E,TROCHIDIS A.Crack identification in double-cracked beams using wavelet analysis[J].Journal of Sound and Vibration,2004,277:1025-1039.
[5] 刘涛,李爱群,丁幼亮.小波分析在结构损伤识别中的应用[J].地震工程与工程振动,2008,28(2):29-35.
[6] 陈建云,王志华.小波分析在圆柱壳结构损伤检测中的应用研究[J].应用力学学报,2007,24(3):456-459.
[7] 张吉刚,刘红绪,胡跃兵.基于模态应变能的桥梁损伤识别[J].四川建筑,2007,27(4):119-121.
[8] 蔡立君,冉红.等离子体破裂时HL—2M 真空室结构应力分析[J].核聚变与等离子体物理,2011,31(2):127-132.
[9] 宋云涛,彭玉华.HALO 电流作用下的EAST 真空室载荷分析[J].核聚变与等离子体物理,2007,27(3):222-226.
[10] 赵玲,李爱群.基于单元应变能变化率的结构损伤识别方法[J].东南大学学报,2007,37(6):1052-1056.
