加权估计方程用于缺失数据的处理

张 伟 冯 萍 赵永红 袁佳英 李 梅

在医学研究过程中缺失数据现象是普遍存在的〔1－3〕，目前实际应用中对缺失值处理的方法主要采用缺失值的删失以及单一填补〔4－5〕。随着统计软件相关程序的实现，更有效的缺失值处理方法逐渐引起研究者的关注，如基于多重填补的方法，基于参数似然的方法以及基于加权估计的方法〔6－7〕。weighted estimating equations(WEE)法是加权估计法中的一种，是广义估计方程(gerneralized estimating equations，GEE)方法的推广，被认为估计效率高，稳健性好，尤其在模型假定错误的情况下，仍可以获得更接近真实值的无偏估计。目前，国际对于缺失数据处理方法的理论应用研究热点多为WEE法〔8－10〕，而国内相对集中于多重填补的研究〔10－14〕，对于 WEE法的研究应用相对较少。因此本文对WEE法的理论框架进行详细介绍。

WEE法最早是由 Robins〔15〕等人于1994年提出的一种与极大似然估计有相似性质的缺失数据处理方法，多用于处理可忽略缺失(ignorable missingness)的情况，也有研究将WEE法用于处理不可忽略缺失数据〔16〕。WEE法的原理是采用某种方式把缺失单元的权数分解到非缺失单元上，通过增大样本观测值的权数以减少由于缺失对估计量可能带来的偏差。

WEE法是在结局变量与协变量间存在线性关系的前提下进行模型构建的，故假设在回归模型中，令Yi表示结局变量，Xi为协变量，i=1，2…n表示样本量，故结局的均值模型为:U=Ui(Xi，β)=E(Yi|Xi，β)，其中β为参数。当没有缺失值时，采用样本数据对总体结局均值进行估计，则有，式中wi为第i个单元的权数，是样本单元入样概率φi的倒数;参数估计方程为|xi))。令u(β)=0，就可得到β的无偏估计。

当存在缺失时，对原权数wi进行调整，以表示调整后权数，则，均值模型变为，其中nobs表示已观测单元的样本量，εi为调整因子，协变量完全观测到的概率πi的倒数，是缺失机制的体现。当缺失机制为完全随机缺失时，πi既不依赖于已观测变量 Xobs，i，也不依赖于缺失变量 xmis，i，即 πi=Pr(ri=1|yi);当缺失机制为随机缺失时，πi仅依赖于 xobs，i，即 πi=Pr(ri=1|yi，xobs，i);当缺失机制为非随机缺失时，πi既依赖于Xobs，i，也依赖于 Xmis，i，即 πi=Pr(ri=1|yi，xobs，i，xmis，i)，其中ri为指示变量，当ri=1表示Xi全部观测，ri=0表示Xi部分观测。

假定在给定(yi，xi)下，ri=1的概率为πi，则有πi= πi(θ)=Pr(ri=1|mi;θ)，其中mi是(yi，xi)的某种函数，以(yi，xi)表示mi，θ为缺失指示变量ri的参数。

当存在缺失时，若仅用观测到的数据估计参数β，则似然估计方程为－u)，上述方程为0时可获得参数的估计，但由于估计方程仅用观测到的数据，因此对β的估计是有偏的。假设协变量全部观测到时的概率πi已知或者可以有效估计出，将 ri替换为 ri/πi，权重变为ri/πi，加权估计方程则变为ui);在随机缺失情形下，上述估计方程的期望对0是无偏的，即

因此令uWEE(β)=0时，可以得到参数β的无偏估计。

在上述估计方程中同时加入未观测数据的信息以提高估计效率获得更有效的无偏估计，若πi能被正确估 计， 则1成立，同时也可得=0。则更有效的无偏估计方程可写为:

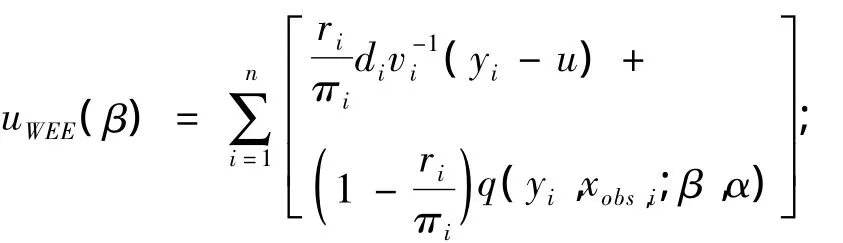
其中 q(yi，xobs，i;β，α)是已观测数据(yi，xobs，i)、β和 α 的一个特定函数:q(yi，xobs，i;β，α)=E［ui(β)|与前述相比，该法增加了部分信息，提高了效率，被认为是更有效的估计方程。但该方程的无偏估计是基于加入缺失信息的准确性，因此需要另一种估计方程来估计α。令 r=(β，α，φ)，则加权估计方程为:

其中 u1i(β)= u1i(β;yi，xobs，i，xmis，i)，u2i(β)=u2i(α;xobs，i，xmis，i)，φ 是 ri的参数。如果缺失变量 xmis，i

为分类时，则:

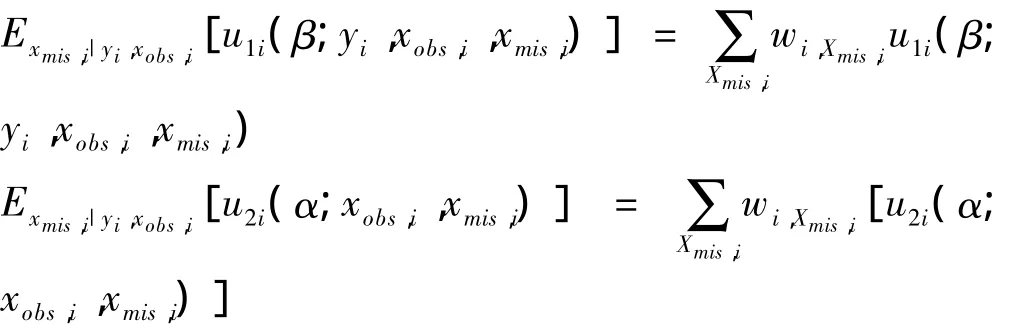
其 中 wi，Xmis，i= P(xmis，i| xos，i，yi，γ) =，为缺失变量 xmis，i在已观测数据(xobs，i，yi)下的条件概率。当缺失变量xmis，i为连续型变量时:

由于上述估计方程与极大似然估计得分方程相似，故 Lipsitz、Ibrahim ＆Zhao〔18〕提出采用 EM 算法或蒙特卡洛EM算法求解S()=0，获得r的无偏估计。具体步骤如下:

(1)设定一个γ初始值，γ=γ(1)，例如以已观测数据计算得。在t步时，有γ(t)。

(2)令 wi，Xmis，i(t)为给定 γ=γ(t)时缺失变量的条件概率，并用 γ(t)计算

(3)将 wi，Xmis，i(t)作为固定值，用可加权的广义线性方程对γ(t+1)求解S(γ(t+1)|γ(t))。

(4)反复上述步骤，迭代至收敛，当γ(t+1)=γ(t)=时，得到)=0的解。

上述加权估计方程公式中包含有三个模型:①目标参数模型:E(yi|xi)=ui(β)，Var(yi)= φVi(β);②缺失机制模型:p(ri|φ;(yi，xi')')=πi;③在给定已观测值下，缺失变量的条件分布模型:p(xmis，i|xobs，i，α)。其中任一个模型被假定正确时，另一模型无论是否正确，对参数的估计是渐近无偏的。对上述方程的性质，有学者〔17，19〕进行了理论证明，结果显示上述加权估计方程具有双重稳健性。

WEE方法是基于加权的处理方法，该法的优势在于其稳健性，能同时实现以下两个目标:①在不完全数据的基础上通过权数调整实现无偏或近似无偏的点估计;②通过权数调整提高点估计的效率，较大限度地降低估计误差。WEE估计方法不需依赖总体参数分布，在一般总体分布下表现良好及稳健。当缺失模型假定错误时，基于参数似然的方法以及基于多重填补的方法的估计结果可能出现偏倚，此时WEE法可以提供稳健结果，但稳健性的代价是参数估计效率会有所降低。但与当总体参数模型假定正确情况的参数似然及多重填补方法相比，WEE法不依据总体分布的估计率却是偏低的。因此，在实际应用中，如果缺失机制能准确假定，如缺失机制为实际上，缺失数据统计分析方法的有效性很大程度上依赖于数据缺失是否与数据集完全随机缺失(missing completely at random，MCAR)时，何种缺失数据处理方法均可，可以采用单一填补或是多重填补等简单方法实现填补;当缺失机制为随机缺失(missing at random，MAR)时，如果对于数据总体分布能准确估计，如总体满足多元正态分布时，基于参数似然的方法以及基于多重填补的方法能获得更为有效的估计;当缺失机制为非随机缺失(not missing at random，MCAR)时，基于参数似然的方法以及基于多重填补的方法不能获得有效估计，此时WEE却能获得稳健结果。所以无论何种缺失处理方法在实际应用中，应综合考虑资料类型、变量类型，以及不同缺失机制等条件下的数据特征，选择适当的方法，以达到较高估计效率，得到渐近无偏估计。

1．Shih W．Problems in dealing with missing data and informative censoring in clinical trials．Current Controlled Trials in Cardiovascular Medicine，2002，3:4．

2．Abraham W，Russell D．Missing data:a review of current methods and applications in epidemiological research．Current Opinion in Psychiatry，2004，17(4):315-321．

3．Selvin S．Statistical analysis of epidemiologic data．2004，Oxford;New York:Oxford University Press．

4．Geert Molenberghs，Kenward MG．Missing Data in Clinical Studies．Paediatric and Perinatal Epidemiology，2007，21(6):552-554．

5．唐健元，杨志敏，杨进波等．临床研究中缺失值的类型和处理方法研究．中国卫生统计，2011，28(3):338-343．

6．Little RJA，Rubin DB．Statistical analysis with missing data．Hoboken，NJ:J Wiley ＆ Sons，2002．

7．Graham JW．Missing data analysis:making it work in the real world．Annu Rev Psychol，2009，60:549-576．

8．Caroline Beunckens，Cristina Sotto，Geert Molenberghs．A simulation study comparing weighted estimating equations with multiple imputation based estimating equations for longitudinal binary data．Computational Statistics ＆ Data Analysis，2008，52(3):1533-1548．

9．Lan Kong，Jianwen Cai，Sen PK．Weighted estimating equations for semiparametric transformation models with censored data from a casecohort design．Biometrika，2004，94(2):305-319．

10．Michelle Shardell，Miller RR．Weighted estimating equations for longitudinal studies with death and non‐monotone missing time‐dependent covariates and outcomes．Statistics in Medicine，2008，27(7):1008-1025．

11．周艺彪，姜庆五，赵根明．不完全数据处理方法:多重填充．中华预防医学杂志，2004，38(6):424-426．

12．花琳琳，施学忠，杨永利．不同缺失值填充技术在HIV/AIDS血液样品检测数据中的应用．中国卫生统计，2011，28(6):668-673．

13．金勇进．调查中的数据缺失及处理(I):缺失数据及其影响．数理统计与管理，2001，20(1):59-62．

14．冯志兰，刘桂芬，刘力生等．缺失数据的多重估算．中国卫生统计，2005，22(5):274-277．

15．Robins J，Rotnitzky A，Zhao L．Estimation of Regression Coefficients When Some Regressors Are Not Always Observed．Journal of the A-merican Statistical Association，1994，89(89):864-866．

16．Carpenter JR，Kenward MG，Vansteelandt S．A comparison of multiple imputation and doubly robust estimation for analyses with missing data．Journal of the Royal Statistical Society:Series A(Statistics in Society)，2006，169(3):571-584．

17．Joseph G，Chen MH，Stuart R．Missing-Data Methods for Generalized Liner Models:A Comparative Review．Journal of the American Statistical Association，2005，100(469):332-346．

18．Lipsitz SR，Ibrahim JG，Zhao LP．A Weighted Estimating Equation for Missing Covariate Data with Properties Similar to Maximum Likelihood．Journal of the American Statistical Association，1999，94(448):1147-1160．

19．Troxel AB，Lipsitz SR，Brennan TA．Weighted Estimating Equations with Nonignorably Missing Response Data．Biometrics，1997，53(3):857-869．