面向LED扩展光源的新型反馈修正设计方法
2013-12-04石智伟闫国栋邓国强王钦若骆徳汉陈益民梁鸣娟祝炳忠
石智伟 闫国栋 邓国强 王钦若 骆徳汉 陈益民 梁鸣娟 祝炳忠
(1.广东工业大学信息工程学院,广东广州 510006;2.东莞勤上光电股份有限公司,广东东莞 523565)
1 引言
由于发光二极管 (Light Emitting Diode,LED)相对于传统照明光源具有节能、环保、使用寿命长、反应速度快等优点,大功率LED照明技术引起了国内外光源界的普遍关注。大功率LED照明产品已成为具有发展前景和影响力的一项高新技术产品,其研制、开发和生产已成为发展前景十分诱人的朝阳产业。由于LED发出的光近似朗伯型,与传统光源有较大不同,不能直接用于现有的照明系统[1~4]。因此,为了更好的将LED作为照明光源,研究大功率LED光源的二次光学系统配光设计,合理分配LED芯片的光能显得尤为迫切。
在当前的LED自由曲面光学设计中,由于目标平面与光源的距离远远大于光源的尺寸,光源的大小与光学系统相比也可忽略,所以常用点光源来近似代替实际光源;通过网格的细分,再结合边缘光线理论,近似认为网格结点代表整个网格。通过这些近似,将实际的问题简单化,最终建立起透镜模型[5~7]。对于大功率LED自由曲面光学设计,由于上述近似,实际得到的仿真结果与预期效果存在较大偏差。
近来,为了减小这些偏差,获得更好的结果,人们引入不同的反馈修正方法[8,9]。但是,这些方法总体来说操作复杂,有的方法得到的结果也较差。本文通过分析整个建模过程,提出了一种基于等差数列的新型反馈优化方法,通过更改光源网格的划分来改变各网格对应的光通量,进而改变目标面的照度分布,与各种误差对模型的影响相抵消,最终得到我们预期的效果。文中以实现花瓣状照度分布的LED透镜优化设计为例验证了该方法,结果表明,该种反馈优化方法不仅操作简单,而且设计的LED自由曲面可以很好的达到预期效果,照明均匀度高,出光效率高。
2 反馈优化方法
2.1 偏差原因分析
为了完成光学设计,在曲线的求解过程中,除了基准线外,其他曲线的求解起始点为基准线上的近似点,导致所求点的实际法向矢量与所计算的法向矢量存在着一定的偏差,并且偏差逐渐增大,使光线并不按照预期的情况照射到目标面,最终影响了目标面上的照度分布。此外,我们对光源和目标面进行有限的网格划分,近似的认为网格结点代表整个网格;整个曲面的求解过程是通过数值解的方法进行的,计算过程中肯定是存在误差的;实际光源近似为点光源;另外还有建模软件和仿真软件的精确性问题等。所有这些原因都导致了结果与我们预期效果存在较大偏差。
2.2 反馈优化设计
反馈优化设计就是通过目标面的照度分布,反过来调整网格对应关系进而使目标面上的照度重新分布以达到预期要求,目标面上照度分布与光通量及照明面积的关系为:
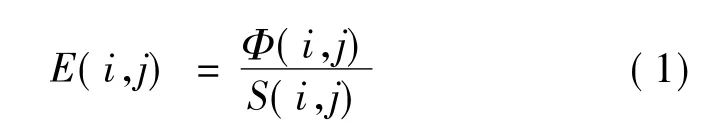
其中,E(i,j)为第 i行,第 j列网格的照度值,Φ(i,j)为照射到该网格的光通量,S(i,j)为该网格的面积。例如目标面某个网格对应的照度为E,而预期值为E0,如果E>E0,就需要将对应光源网格缩小以减少其光通量或者增大目标面的网格以增大照射面积从而降低该网格的照度值,反之,则需增大光源网格以增大其光通量或者减小目标面的网格以减小照射面积从而增大该网格的照度值。
当前有一些解决目标平面照度不理想的问题的反馈优化算法,其通常是依据仿真的照度分布与预期照度分布的关系求得各网格的反馈系数,得到反馈系数矩阵,在能量对应关系中添加反馈系数,重新建立新的对应关系进行曲面离散点的求解,如此反复,最终达到预期的设计目的。这种方法反馈系数矩阵的求解很麻烦,并且该方法一般要经过多次反复优化,大大增加设计过程的工作量。本文提出一种新的基于等差数列的反馈优化方法,该方法根据偏差对照度分布连续影响的特点,引入以等差数列形式分布的反馈系数对设计进行优化。实验表明,该方法操作简单,大幅减少设计过程的工作量,并且可以达到很好的优化效果。
2.2.1 正向反馈优化方法
正向反馈优化方法是对光源的网格划分不变,通过目标面网格的扩大与缩小来调整照度分布情况。在光源网格划分不变的情况下,与该网格对应的光通量是不变的,由公式 (1)可知,通过改变目标面网格的面积可以调整该网格的照度分布。根据仿真得到的照度分布,沿某一照度分布存在偏差的方向引入项数为M的等差数列a1,a2,a3,…,aM做为反馈系数,M也为需要调整的区域沿选定方向划分的网格数,则其前n项和为:
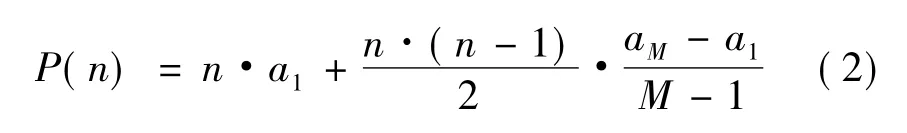
则经过调整后,目标面上各网格的面积为:
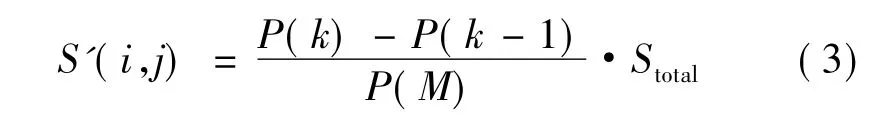
其中,S'(i,j)为优化调整后目标面上第i行,第j列网格的面积,Stotal为所需调整区域的总面积。若沿横向方向调整优化,则k=i,若沿纵向方向,则k=j。如果需要调整的区域沿选定方向照度由偏大变化到偏小,则等差数列的初值选取应为a1>aM,否则应选取为a1<aM。图1所示为一种目标面按照以等差数列分布的反馈系数调整前后示意图,经调整后,目标面左边照度分布相比于调整前有所增加,而右边则有所减小。
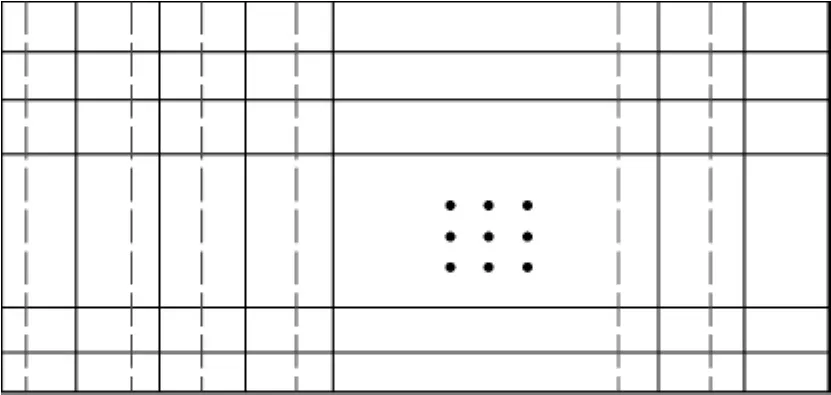
图1 目标面网格调整前后示意图Fig.1 The adjustment of mesh grids of the target surface
2.2.2 逆向反馈优化方法
逆向反馈优化方法是对目标面的网格划分不变,通过对光源网格划分的改变来调整目标面的照度分布。由公式 (1)可知,在目标面网格照明面积不变情况下,通过改变照射到该网格的光通量可以调整其照度分布。同样的,在沿某一照度分布存在偏差的方向引入项数为M的等差数列b1,b2,b3,…,bM做为反馈系数,则经过调整后,光源各网格的光通量为:
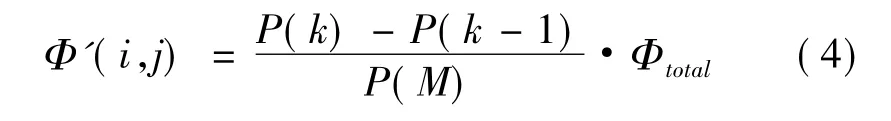
其中,Φ'(i,j)为优化调整后光源划分第i行,第j列网格的光通量,Φtotal为需调整区域的总光通量。图2所示为一种光源网格按照以等差数列分布的反馈系数调整前后示意图,经图2所调整后,目标面中心部分光通量相比于调整前有所增加,而四周边缘部分则有所减小。
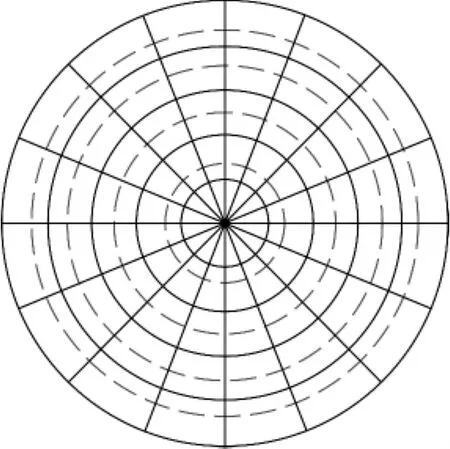
图2 光源网格调整前后的示意图Fig.2 The adjustment of mesh grids of the light source
前面所述两种反馈优化方法所采取的原理基本相同,但采用的实施手段不同。我们可根据实际情况选取一种较易实现的方法,也可把这两种方法结合使用以达到更好的优化结果。
3 设计实例
本实例设计一个成花瓣状照度分布的LED透镜,在距离光源10m远处的目标面上形成四片如图3(b)所示半径为20m的花瓣并要求四片花瓣部分照度均匀。在本实例的模拟仿真中,选用科锐公司XPG系列的LED芯片作为光源,其发光面的尺寸约为1mm,具有近似朗伯型的发光面,透镜材料选用PMMA,其折射率约为1.49。具体设计步骤如下:
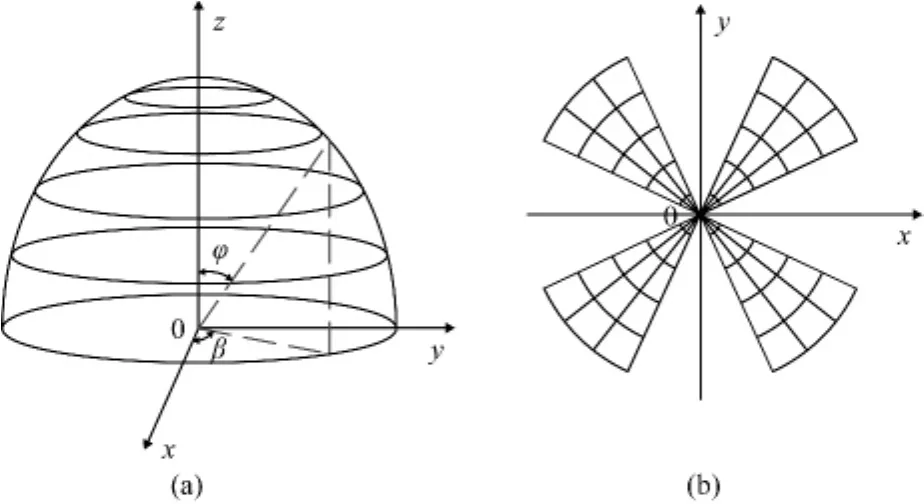
图3 光源网格与目标面网格对应关系Fig.3 The corresponding relationship between the light source and target surface
(1)采取图3所示划分方式对光源和目标面进行网格划分,建立相应网格点的对应关系:(φi,θj)-(xi,yj),其中,φ为光线出射方向与LED芯片平面法向方向(即z轴正向)的夹角,θ为出射光线在xy平面上的投影与x轴正向的夹角。
(2)按照建立的对应关系进行表面数据点的迭代求解,得到初始透镜模型数据点(图4),并对所建模型仿真分析(图6(a))。
(3)将分析仿真结果与预期效果对比分析,确定具体优化方案。本例中由图6(a)可以看出初始模型的照度分布为中心部分比较暗,而向边缘部分逐渐增强,所以我们按等差数列的分布方式重新划分光线方向与LED芯片平面法线方向(即z轴方向)的夹角φ ,引入项数为 M 的等差数列 a1,a2,a3,…,aM,取a1=1.5,aM=0.5,则重新划分的 φ'(i)为 φ'(i)=
φ'(i-1)+φ(i)(P(i) -P(i-1)) P(M)。
(4)按照步骤(3)的划分重新建立网格点的对应关系 (φ'i,θj) - (xi,yj);
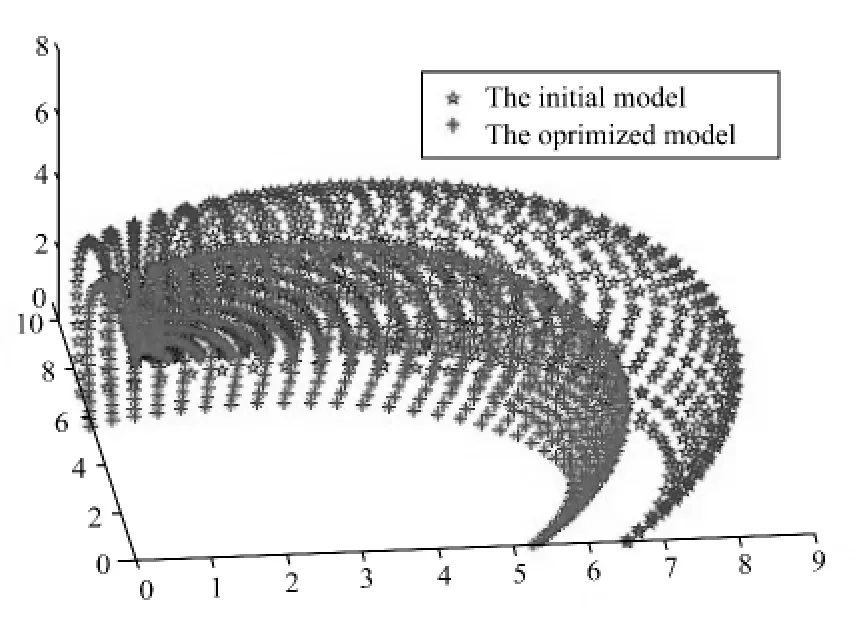
图4 优化前后光学系统表面数据点对比Fig.4 The initial and optimized optical system models
(5)按照新建立的对应关系进行表面数据点的迭代求解,得到优化后的透镜模型(图5),并对所建模型仿真分析(图6(b))。

图5 优化后的3D模型Fig.5 3-D geometry of the optimized optical system model
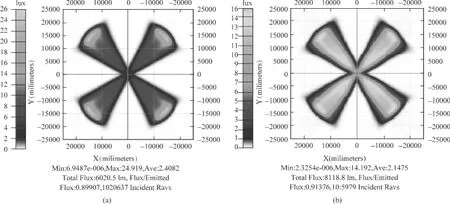
图6 优化前后仿真结果Fig.6 Simulation result of(a)the initial modes and(b)the optimized modes
图6 为初始模型与优化后所得模型仿真结果的照度分布对比图。从图6可以看出,初始模型仿真所得照度图中边缘部分有明显亮斑,与预期结果存在较大差距,而优化后所得模型有较好的仿真结果。定义照度均匀度为照明区域最小照度与平均照度之比,即U=EminEav,优化所得模型的照度均匀度达到了92.3%(其最小照度Emin和平均照度Eav分别约为12lx和13lx)。最终设计模型的尺寸(长,宽,中心高度)为13.9mm×13.0mm×6mm。
4 结论
本文通过对透镜设计方法的研究及整个建模过程的分析,提出了一种基于等差数列的反馈优化方法,并用此方法完成了花瓣状照度分布LED透镜的优化设计,得到了分布均匀的花瓣状照度图,结果表明,该种反馈优化方法简单易操作,用该种方法进行的透镜优化设计可以很好的达到预期效果,并且适用于各种不同的设计场合。
[1]M.A.Moiseev,L.L.Doskolovich,N.L.Kazanskiy.Design of high-efficient freeform LED lens for illumination of elongated rectangular regions.Opt.Express 19(S3),A225~A233(2011).
[2]K.C.Lin.Designation of lenses with a single freeform surface for multiple point sources.J.Opt.Soc.Am.A,29(3),200~208(2012).
[3]Y.Ding,X.Liu,Z.R.Zheng,P.F.Gu.Freeform LED lens for uniform illumination.Opt.Express 16(17),12958~12966(2008).
[4]H.Ries,J.Muschaweck.Tailoring freeform lenses for illumination.Proc.SPIE.4442,43~50(2001).
[5]K.Wang,F.Chen,Z.Y.Liu,X.B.Luo,S.Liu.Design of compact freeform lens for application specific light-emitting diode packaging.Opt.Express 18(2),413~425(2010).
[6]K.Wang,D.Wu,Z.Qin,F.Chen,X.B.Luo,S.Liu.New reversing design method for LED uniform illumination.Opt.Express 19(S4),A830 ~A840(2011).
[7]Y.Ding,X.Liu,Z.R.Zheng,P.F.Gu.Secondary optical design for LED illumination using freeform lens.Proc.SPIE 7103,71030K(2008).
[8]W.C.Situ,Y.J.Han,H.T.Li,Y.Luo.Combined feedback method for designing a free-form optical system with complicated illumination patterns for an extended LED source.Opt.Expreess 19(S5),A1022 ~A1030(2011).
[9]Y.Liu,K.Wang,S.Liu.Freeform Lens Design for Uniform Illumination with Extended Source.ICEPT-HDP 2011 Proceedings.New Jersey:IEEE Computer Society,1085~1089(2011).
