电荷量子化介观LC电路的准经典解
2013-12-03林琨智
林琨智,刘 艳,何 畏
(1.吉林工业职业技术学院,吉林 吉林 132108;2.吉林化工学院 理学院,吉林 吉林 132021;3.华北电力大学 国际教育学院电气工程及其自动化系,北京 102206)
近年来,关于介观电路量子效应的研究已引起人们广泛关注[1-4],基于电荷量子化建立的介观电路理论[5],采用绝热近似,将电源作为常数处理,给出介观电路的定态解.由于含电感和电容介观电路中的电流强度和电压是时间的函数,因此,若电路的量子态处于不同本正态的叠加,则其实验可测量值为力学量的平均值.本文在文献[5-6]的基础上,以LC串联电路为例,采用介观电路准经典描述[7]力学量平均值随时间的演化规律,给出描述电荷量子化介观电路的准经典方法.
1 电流强度的平均值
经典有源LC串联电路的运动方程为
(1)
其中:q为电荷;L为电感;C为电容;ε(t)为外加电源.其对应的Hamilton量为
(2)


ћ.
(3)
(4)
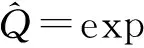
(5)
在p表象中动量算符定义为
(6)
自由Hamilton算符定义为
(7)
Hamilton算符为
(8)
对于介观LC电路

(9)
(10)
这里{·,·}表示反对易.使式(10)等号成立的条件为

(11)
根据相干态是最小不确定态的性质,式(10)应取等号,即
(12)

(13)
利用式(5),(6)及Q的定义可得:
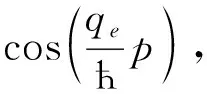
(14)
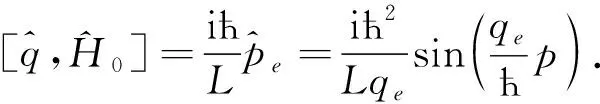
(15)
LC介观电路满足Schrödinger方程

(16)

(17)
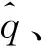
(18)

(19)


(20)

(21)

(22)
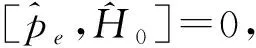
(23)
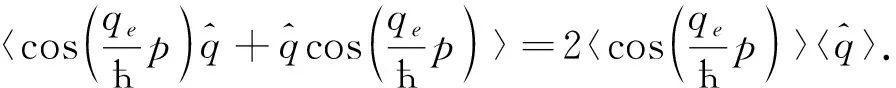
(24)
将式(18)和式(24)代入式(19),式(23)代入式(20)得:
(25)

(26)
将式(25)除以式(26)可得
(27)

(28)
由式(18),(25),(28)可得LC介观电路电荷平均值满足的非线性方程为
(29)

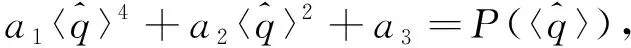
(30)
其中:

(31)
将式(31)对t微分得电流强度的平均值为
(32)
取cn(ωt)的实周期K,当时间t满足
(33)
时,式(32)不为零.其中
(34)
若电源给LC电路电容充电的电荷数为基本电荷的整数倍,则在任意时刻电路中都不应出现基本电荷的分数情况.即
(35)
将式(35)代入式(31)可得
(36)
2 相干态波函数
由式(11),(12)可得[9]
(37)
将式(37)代入式(11)可得
(38)

(39)
将式(14),(18)代入式(39)可得
(40)
令

(41)
移项得
(42)
由相干态为满足最小不确定态的表述
(43)
中求出(Δq)2并代入式(42)可得
(44)
由于(Δpe)2为小量,因此式(44)中第二项的量比第一项更小,故舍去.令其等于零可得
(45)
将式(45)代入式(43)可得
(46)
将式(45)代入式(40)可得相干态波函数为
(47)

ψ(p,t)=eiθ(p,t)φ(p,t),
(48)
其中θ(p,t)为实数.
由于ψ(p,t)为归一化波函数,因此代入式(47)可得
(49)
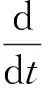
(50)
式(50)乘以dt并积分得
(51)
3 准经典波函数
由于电荷和电流强度平均值与相干态波函数存在的前提是存在满足Schrödinger方程式(16)的准经典波函数式(48),因此若θ(p,t)存在,则式(48)成立.将式(47)代入式(48)后再代入式(16),并令等式两端的实部和虚部对应相等,可得:
(52)

(53)
其中:

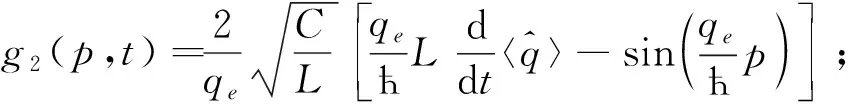
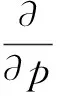
(54)

(55)
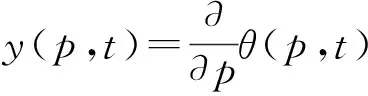
(56)

式(56)为Riccati方程,该方程存在y(p,t)的解,从而可得
(57)
将式(57)代入式(52),(53)可得h1(t),证明ψ(p,t)=φ(p,t)eiθ(p,t)存在.
当qe→0时,由式(29),(51),(47)分别得:
(58)

(59)

(60)
将式(59)代入式(60)可得归一化概率密度为
→0.
(61)
式(58)和式(61)与文献[7]的结果相符.
综上所述,本文以LC介观电路为例,利用电荷量子化介观电路中电荷和广义电流满足的对易关系、 波函数遵循的Schrödinger方程和力学量平均值随时间演化公式,给出了相干态波函数满足的微分方程,形成了描述电荷量子化介观电路的准经典方法.
[1] Garcia R G.Atomic-Scale Manipulation in Air with the Scanning Tunneling Microscope [J].Appl Phys Lett,1992,60(16): 1960-1962.
[2] Landeuer R.Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction [J].Res Dev,1957,1(3): 223-231.
[3] Louisell W H.Quantum Statistical Properties of Radiation [M].New York: John Wiley,1973: 90-124.
[4] 凌瑞良,冯金福.熵、 量子与介观量子现象 [M].北京: 科学出版社,2008: 122-128.
[5] LI You-quan,SHA Jian,ZHANG Qi-rui,et al.Quantum Effects of Charge in the Mesoscopic Circuit [J].Acta Phys Sinica,1997,46(1): 129-133.
[6] 倪光炯,陈苏卿.高等量子力学 [M].上海: 复旦大学出版社,2000: 29-42.
[7] LIN Kun-zhi,LIU Yan.Quasi-classical Description of Mesoscopic Circuit [J].Journal of Jilin University: Science Edition,2011,49(3): 523-527.(林琨智,刘艳.介观电路的准经典描述 [J].吉林大学学报: 理学版,2011,49(3): 523-527.)
[8] 刘式适,刘式达.特殊函数 [M].2版.北京: 气象出版社,2002: 620-630.
[9] YAN Zhan-yuan.Quantum Effects in Mesoscopic Circuits [D].Baoding: North China Electric Power University,2007.(阎占元.介观电路量子效应的研究 [D].保定: 华北电力大学,2007.)
