广义延拓矩阵的LDU分解和Cholesky分解
2013-12-03伍亚魁吴桂权简芳洪
伍亚魁 吴桂权 简芳洪
(1九江学院理学院 江西九江 332005;2九江市彭泽县第一中学 江西彭泽 332700)
现实生活中,很多实际问题,都可转化成数学线性问题,进而利用矩阵解决.文献[1-4]提出延拓矩阵的概念,文献[5]在此基础上提出广义延拓矩阵.文献[6,7]提出行(列)对称矩阵,并根据母矩阵的LDU分解、Cholesky分解和三对角分解给出行(列)对称矩阵的LDU分解、Cholesky分解和三对角分解公式[8].本文在文献[6,7]的基础上给出了广义延拓矩阵的LDU分解、Cholesky分解和三对角分解的公式,可极大地减少广义延拓矩阵的LDU分解、Cholesky分解和三对角分解的计算量与存储量,而且不会丧失数值精度,从而拓宽了文献[1~4]的理论应用范围.
1广义延拓矩阵的概念

A称为R(A;P1,P2,…,Pk-1)的母矩阵.
定义2[1,2,5](广义列延拓矩阵) 令A∈Rm×n,可逆矩阵P1,P2,…,Pk-1∈Rn×n,k为任意给定的正整数.定义广义列延拓矩阵C(A;P1,P2,…,Pk-1)为:
C(A;P1,P2,…,Pk-1)=[A,AP1,AP2,…,APk-1]∈Rm×kn
A称为C(A;P1,P2,…,Pk-1)的母矩阵.
注:(1)当P1=P2=…=Pk-1=I(单位矩阵)时,R(A;P1,P2,…,Pk-1)为文献[1]的第一类k次行延拓. 当P1=P2=…=Pk-1=P(置换矩阵)时,R(A;P1,P2,…,Pk-1)为文献[2,3]的第二类k次行延拓.
(2)当P1=P2=…=Pk-1=I(单位矩阵)时,C(A;P1,P2,…,Pk-1)为文献[1]的第一类k次列延拓. 当P1=P2=…=Pk-1=P(置换矩阵)时,C(A;P1,P2,…,Pk-1)为文献[2,3]的第二类k次列延拓.
由以上定义,显然有以下结论.
性质1[1,2,5](保秩性)
rankR(A;P1,P2,…,Pk-1)=rankC(A;P1,P2,…,Pk-1)=rank(A).
性质2[1,2,5](转置关系)
性质3[1,2,5](矩阵相乘关系)
XC(A;P1,P2,…,Pk-1)=C(XA;P1,P2,…,Pk-1).
2 广义延拓矩阵的几种分解
2.1 LDU分解

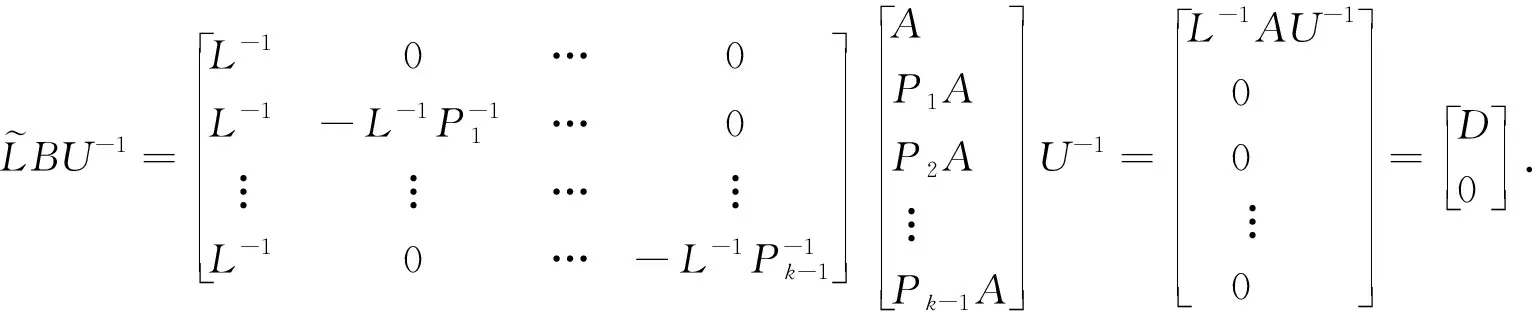
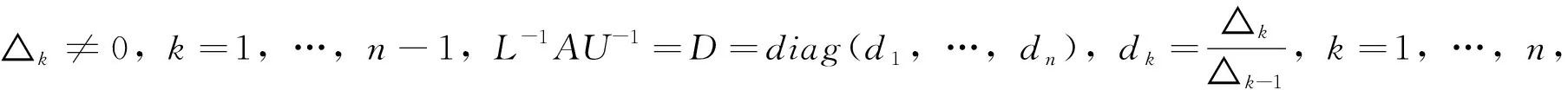

2.2 Cholesky分解


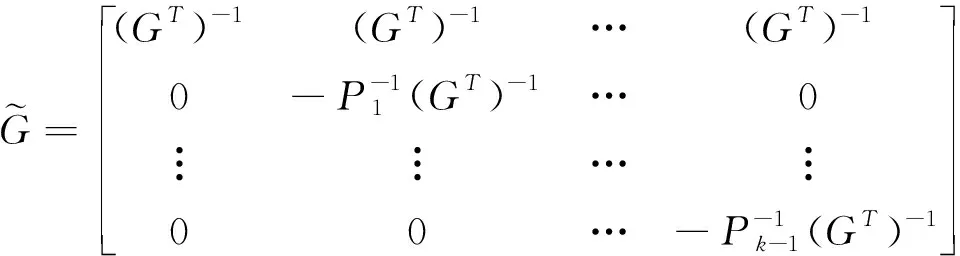
证明:
=[G-1A(GT)-1,0,0,…,0]=[In,0].
2.3 三对角分解



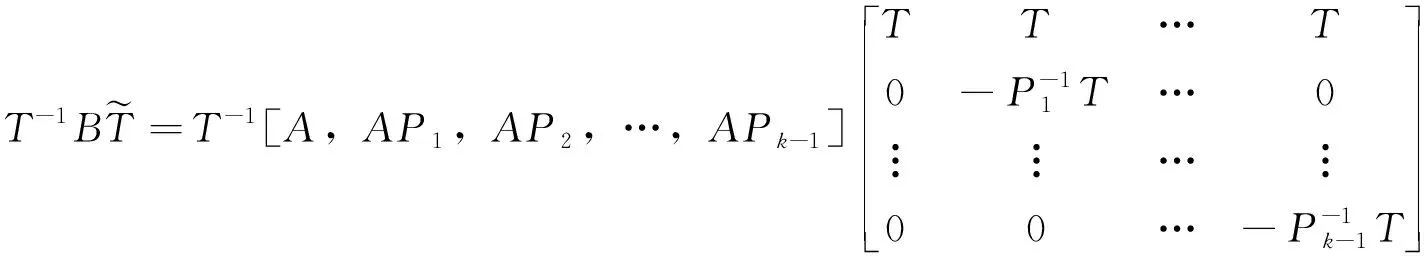
=[T-1AT,0,0,…,0]=[C0]
参考文献:
[1]邹红星,王殿军,黛琼海,等.延拓矩阵的奇异值分解[J].科学通报,2000,45(14):1560.
[2]邹红星,王殿军,黛琼海,等.延拓矩阵的奇异值分解[J].电子学报,2001,29(3):289.
[3]邹红星,王殿军,黛琼海,等.行(或列)对称矩阵的QR分解[J].中国科学(A),2002,32(9):843.
[4]蔺小林,蒋耀林. 酉对称矩阵的QR分解及其算法[J].计算机学报,2005,28(5):817.
[5]许成锋 刘智秉,王侃民,等. 广义延拓矩阵的QR分解[J].九江学院学报(自然科学版),2009,29(6):78.
[6]袁晖坪.行(列)对称矩阵的LDU分解和Cholesky分解[J].华侨大学学报(自然科学版),2007,28(1):88.
[7]袁晖坪.行(列)对称矩阵的满秩分解和正交对角分解[J].上海理工大学学报,2007,29(3):260.
[8]张贤达. 矩阵分析与应用[M].北京:清华大学出版社,2004.225.
