考虑板坯设计的组炉优化模型

杜 斌，朱 俊，贾树晋，刘士新

（1.东北大学 信息科学与工程学院，辽宁 沈阳110004；2.宝钢研究院自动化所，上海201900）

炼钢组炉问题属于炼钢－连铸段的生产批量计划中的炉次计划问题［1－2］.由于工艺原因，计划人员必须将不同的合同组织到同一炼钢炉进行生产，炉中合同必须满足如下几个条件：①炉中各合同所采用的钢级（steel grade）必须相同；②炉中各合同所采用板坯规格（厚度、宽度）必须相同，这是下游的连铸工序约束；③设炉中某合同总质量为X，则必存在某整数N，使X／N落在合同要求的板坯质量上下限范围内；④炉内合同总量不得超过炼钢炉最大生产容量，在炼钢生产中，若某炉的合同量不满一炉时，仍然需要以一炉的量进行组织生产，一炉中没有合同对应的多余产量称为余材［3］.

组炉优化的一般流程如下：首先按照合同要求进行板坯规格设计，确定合同所需要的板坯的数量以及板坯规格，之后按炼钢组炉的要求将不同的板坯归并到一个炼钢炉进行生产，并确定板坯所选择的钢级（即对应炼钢炉的钢级）.各合同均设计有一系列可选择的钢级，分别称为主钢级、副钢级，使用主钢级的生产成本最低，但有时候为减少余材的产生，也会选择副钢级进行生产［4］.

对于组炉优化问题，学者们做了很多研究，其中Tang等［2］研究了炼钢组炉优化与连铸组浇优化问题，该模型考虑了多个目标（数量级不同）并通过加权方法转化为单目标，但其权重系数的确定是一大难题.黄可为等［3］以板坯为基础分别建立了不考虑副钢级取代成本与考虑副钢级取代成本的数学模型，给出了基于动态规划算法的求解方案.朱俊等［4］则以合同为基础建立了多目标混合规划数学模型，并给出了结合PBIL（population－based incremental learning）算法与网络最大流算法的求解方案，该方法未考虑板坯质量限制.唐立新等［5］同样从板坯出发，给出了综合考虑交货期与钢级取代成本的对应模型，并给出了基于遗传算法求解方案.本文从合同出发，同时考虑板坯设计［6－7］的合理性，建立统一的多目标混合整数规划模型，并结合匹配算法、网络最大流算法以及装箱算法设计出一套启发式算法.试验分析表明，该算法能快速找到组炉优化问题的较优解，适合现场应用.

1 优化模型

炼钢组炉问题可描述为：有M个规格要求相同且属于同一钢级序列的合同O＝｛o1，o2，…，oi，…，oM｝，钢级序列为G＝｛g1，g2，…，gk｝，合同oi所允许的钢级集合为Gi，Gi⊆G，其中一个钢级为主钢级，其余为副钢级，订货量为mi，最少供货量为mi，min，最大供货量为mi，max，合同要求板坯最小质量Ui，min，最大质量为Ui，max，i＝1，2，…，I.炼钢炉每炉最多炼钢质量为Mmax，最少炼钢质量为Mmin，若某炉炼钢质量在Mmin～Mmax范围内，则认为余材量为零.要求合理组织炉次，使炼钢余材量最少，并尽量减少副钢级的使用.

为方便建模，现假设至多需要J个空炉，各炉具有唯一的冶炼钢级属性，即若某合同归并到某炉进行冶炼则必须按照该炉的冶炼钢级进行生产.设各合同采用不同炉次进行冶炼的单位代价成本为cij，i＝1，2，…，I，j＝1，2，…，J，若合同i不能采用炉j进行生产，则cij＝＋∞.据此，建立以下混合整数规划数学模型：

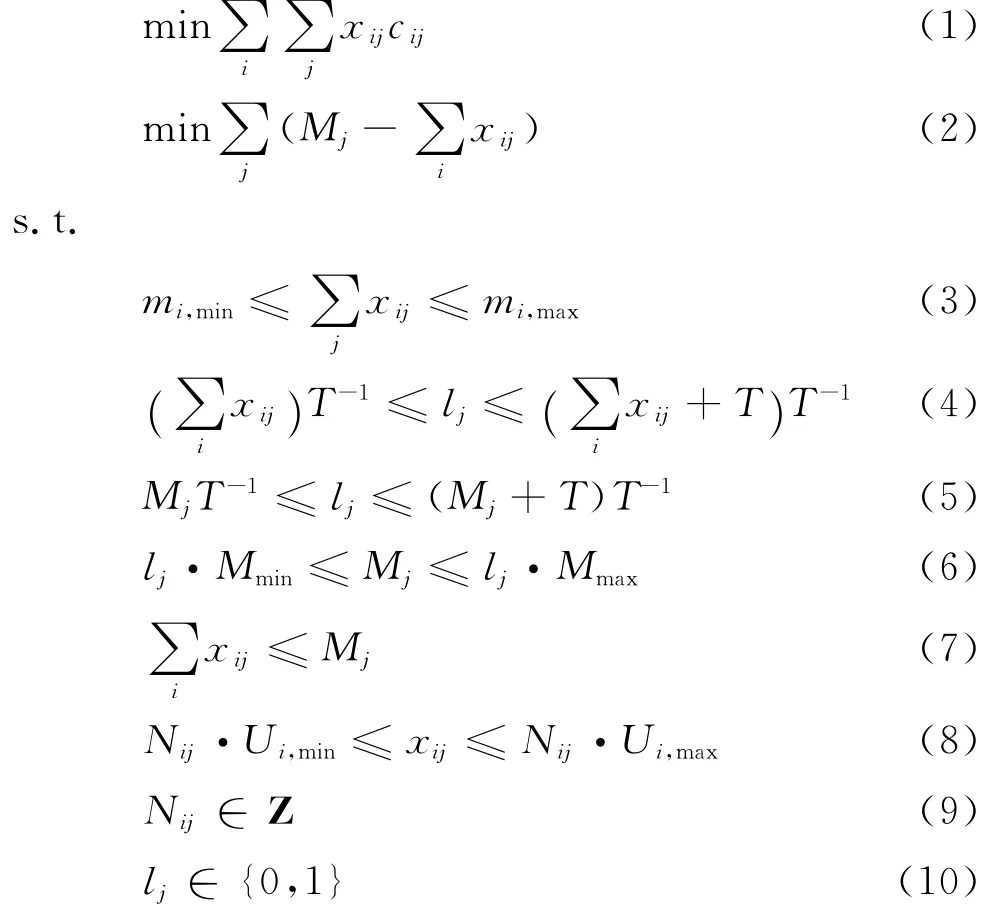
式中：xij为第i个合同匹配到第j个炉的钢的质量；Mj为中间决策变量，表示第j炉的炼钢质量，当lj＝0时Mj＝0，当lj＝1时Mmin）；T为某极大常数；lj为变量，标志第j炉的使用情况，若有合同采用该炉进行冶炼，则为1，否则为0；Nij为第i个合同在第j炉中的板坯数.

该模型共有2个目标，分别是：目标1副钢级成本最低，目标2炼钢总余材量最少.

各约束式含义如下：式（3）表示合同生产量在其供货公差上下限内；式（4）～（7）表示若某炉生产量大于零，则Mmin），否则lj＝0，Mj＝0；式（8）、式（9）表示板坯的单重约束；式（10）为lj的变量约束.

上述模型是一个多目标优化模型，在实际生产中这2个目标的优先级不同，一般来说成本的优先级高于余材，主要是因为余材可以通过余材充当等方式进行消耗，而高的生产成本则难以通过其他方法挽回.

若不考虑钢级约束，则该问题可转化为使余材量最少的单目标优化问题，为Bin－packing问题的一种特殊形式.由于Bin－packing问题属于NP－hard问题［8－9］，故本问题也为NP－hard问题.

2 一种基于匹配的启发式算法

求解NP－hard问题的常用算法主要包括遗传算法、精确算法（小规模问题）以及启发式算法等.由于启发式算法具有计算速度快、灵活性强、可借鉴现场经验等优点，因此从工业应用角度来讲应用最广.基于此本文设计了一种基于最大匹配原理、装箱算法及网络最大流的启发式算法.算法流程如图1所示，其中非二分图匹配算法用于确定炉次；二分图算法与装箱算法用于将剩余合同匹配到已有的炉次中；网络最大流算法用于调整炉次中合同对应的板坯质量，以减少余材量；最后过滤筛选掉余材量过大的炉次.

步骤1：非二分图匹配.对于给定的合同，可按照以下方法构造一个合同兼容性图G＝（V，E）：对于每个合同oi，存在一个节点vi∈V.如果2个合同oi，oj可以组成一炉（属于同一钢级序列），则增加边e＝（vi，vj），合同oi，oj的匹配量可通过求解以下混合规划问题得到.

其中：xi，xj为合同oi，oj的质量；ni，nj为合同oi，oj的板坯数.e＝（vi，vj）的权重wij代表2个合同oi，oj的匹配度，即oi，oj在一炉中冶炼的代价，代价越小越好.假设合同oi的钢级优于oj，那么oi，oj组成的炉次必须按照oi的钢级生产，反之，则炉次须按照oj的钢级生产，生产中称之为“以优充次”.设cij表示合同oi，oj组成一炉的单位代价，则令，若oi的钢级优于oj，那么wij＝c′ijxj，否则wij＝

图1 基于匹配的启发式算法Fig.1 A matching－based heuristic

如图2所示，非二分图G的最大权重匹配M意味着：①匹配的合同oi，oj是兼容的，即可以组成一炉；②每个合同最多只能出现在一炉中；③匹配的总权重最大.通过非二分图匹配算法［7］可以获得G的最大权重匹配M，得到｜M｜个初始炉次.如果总匹配等于零，结束程序，否则，转步骤2.

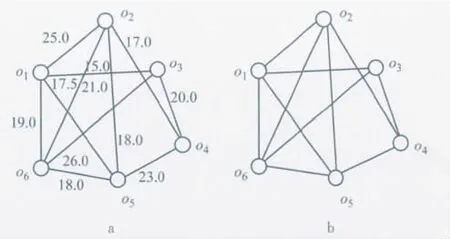
图2 由合同之间构成的最大权重匹配非二分图Fig.2 Maximum weight non－bipartite matching between orders

步骤2：二分图匹配.该步骤循环地构建一个以剩余合同与炉次为节点的二分图并寻找其最大权重二分图匹配［10］，算法步骤如下：①根据步骤1得到的结果，令Ri表示合同oi的剩余质量，Rj表示炉次j的剩余质量；②以剩余合同与已有炉次为节点，构造一个如图3所示的二分图G，左侧节点为剩余合同oi，右侧节点为构造的炉次fj.如果合同合同i与炉次j兼容，则增加一条边e＝（i，j），匹配重量为wij.③令Rij＝min｛Ri，Rj｝，对于合同i与炉次j，令合同i匹配到炉次j中的板坯数为板坯尺寸为的权重为wij＝c′ij·Rij.④在G中寻找一个最大加权二分匹配，如果总的匹配为零，则转步骤3；否则，将Rij质量的合同i匹配到第j个炉次中，且令Ri＝Ri－Rij，Rj＝Rj－Rij，转回步骤2继续执行.

图3 由合同与炉次构成的权重匹配二分图Fig.3 Weighted bipartite matching between order and furnace

步骤3：装箱算法.该步骤模拟一维装箱过程，将之前所获得的炉子视为箱子，以剩余合同物件进行装箱.步骤为，①根据步骤2得到的结果将剩余合同oi划分成质量为Ui，min的板坯.②采用Best－Fit算法进行装箱，具体步骤为令i＝l；对合同oi，依次从当前可用炉次集合中寻找一个成本最低的炉次，即炉次钢级属于板坯主副钢级之一，且炉次剩余质量Rj大于合同剩余质量；令i＝i＋1，如果i＜I，重复以上操作；否则算法终止.

步骤4：调整板坯质量.本步骤通过增加板坯大

小来进一步减少余材.由于步骤2、步骤3板坯并不是依据最大坯重进行设计，故存在一定的调整空间.算法步骤为，①统计之前各合同所匹配的板坯数Pnumber，i以及匹配质量Wappweight，i；②构 建 最 大 流 网络［11］如图4所示.该网络为4层有向网络，输入层仅含一个输入节点，且与合同层所有节点相连，输出层仅含一个输出节点，炉次层所有节点均与输出节点相连.合同层由所有在之前步骤中参与匹配且未完成的合同组成，每一个节点代表一个合同.炉次层由步骤1中产生的炉子组成，每一个节点代表一个炉次.若某合同oi有板坯匹配到某炉子fj，则该合同对应节点与炉子对应节点相连.③设定网络中各炉容量.输入节点到第i个合同节点的弧的容量为Pnumber，i·Uimax－Wappweight，i；所有炉子节点到输出节点的弧容量为剩余炉容量Rj；设第i个合同匹配到第j个炉子的质量为Wappweight，ij，板坯数Pnumber，i，则第i个合同节点匹配到第j个炉子节点的弧的容量为Pnumber，ij·Uimax－Wappweight，ij；④通过计算网络最大流，若第i个合同节点匹配到第j个炉子节点的弧的容量大于Wappweight，ij，则可增加板坯质量.然后转步骤5.

图4 最大流网络Fig.4 Maximum flow network

步骤5：过滤筛选.依次检查匹配好的各炉，若某炉的余材量超过设定阀值，则将该炉内板坯重新放回合同，抛弃该炉，返回步骤1.考虑到算法的收敛，算法过程中对阀值进行动态调整，逐步增大阀值.

3 实例计算

现以某钢厂实际生产数据为例，如表1 所示共有13个合同，以第1 个合同为例，若采用主钢种1生产，则其额外单位质量成本为零，若采用副钢种3生产，则其额外单位质量成本为4.炼钢炉的容量上下限分别为290t与310t.

启发式算法采用C＋＋编程实现，在CPU 2.20 GHz、内存1GB 的配置下可在2s内运算得到表2所示结果.表中第5列表示该炉的合同构成，如第1个炉次“1（28.5，2），2（261.5，17）”表示该炉中包含第1个合同28.5t共计2块板坯、第2个合同261.5 t共计17块板坯.从表2可知，第3，4，5，11，12炉中存在余材，共计400t，第9炉中合同8采用副钢种生产，共13t，额外生产成本为26.

表1 合同信息Tab.1 Order information

表2 启发式算法得到的组炉优化结果Tab.2 Charge optimization results by using heuristic method

目前，现场较多采用的是基于规则的人工经验方法，原理如下：

（1）对所有合同以主钢级分类并以每类的主钢级进行组炉.如主钢级Gi类总质量为wi，则可组成［wi／W］炉，其中，W为一炉最大的生产量，剩余量为Ri.

（2）对剩余量Ri依可替代钢级进行合并，尽可能组成1炉，不够1炉的，仍以1炉生产，多余的为余材.

表3为启发式算法与人工经验方法的优化结果对比，从中可以得到以下结论：

（1）针对相同的合同，启发式算法得到的板坯数量较少，说明单位板坯质量较大，减少了板坯切割次数和切割损失，提高了生产效率，且有利于产品运输.

（2）启发式算法可有效降低炉次数，减少了冶炼准备时间，提高了生产效率.

（3）启发式算法得到的组炉方案冶炼成本较低，说明大部分合同采用主钢级生产、少数合同采用“以优充次”的副钢级生产有效降低了生产成本.

（4）启发式算法可有效降低余材量，有利于减少库存，增加流动资金，从而提高经济效益.

（5）从计算效率来看，人工经验方法可在很短的时间内给出组炉方案，效率较高；启发式方法的计算时间在秒级，在实际生产中完全可以接受.

表3 启发式算法与人工经验方法的组炉优化结果对比Tab.3 Comparison of charge optimization results between our method and artificial experience method

从以上分析可知，启发式算法在优化效果上远远优于人工经验方法，在计算效率方面稍弱于人工经验方法，因此本文的方法能在较短的时间内得到好的组炉方案，对实际生产有指导意义.

4 结语

针对炼钢组炉计划编制问题，从合同出发，同时考虑板坯设计问题，建立了统一的多目标混合整数规划模型，并结合匹配算法、装箱算法及网络最大流算法设计出一套启发式算法.通过实际生产数据的仿真研究表明，该算法能在较短的时间内给出合理的组炉方案，在减少余材量的同时减少了炼钢生产成本，有利于减少库存，提高生产效率.

［1］ Smith A，Smith B.Constraint programming approaches to a scheduling problem in steelmaking［C］／／University of Leeds School of Computer studies Research Report Series.Leeds：Leeds School Press，1997：1－10.

［2］ Tang L X，Wang G S.Decision support system for the batching problems of steelmaking and continuous－casting production［J］.Omega，2008，36（6）：976.

［3］ 黄可为，卢克斌，汪定伟.炼钢组炉问题优化模型及其动态规划算法［J］.东北大学学报：自然科学版，2006，27（2）：138.HUANG Kewei， LU Kebin， WANG Dingwei. Dynamic programming algorithm and optimization model of charge design for steel－making［J］.Journal of Northeastern University：Natural Science，2006，27（2）：138.

［4］ 朱俊，贾树晋，杜斌.基于PBIL与网络最大流的组炉算法［J］.东北大学学报：自然科学版，2012，33（1）：52.ZHU Jun，JIA Shujin，DU Bin.PBIL and maximum－flow based algorithm of charge design problem［J］.Journal of Northeastern University：Natural Science，2012，33（1）：52.

［5］ 唐立新，杨自厚，王梦光.炼钢－连铸最优炉次计划模型与算法［J］.东北大学学报：自然科学版，1996，17（4）：440.TANG Lixin，YANG Zihou，WANG Mengguang.Model and algorithm of furnace charge plan for steelmaking－continuous casting production scheduling［J］.Journal of Northeastern University：Natural Science，1996，17（4）：440.

［6］ Heinz S，Schlechte T，Stephan R，et al.Solving steel mill slab design problems［J］.Constraints，2012，17：39.

［7］ Dawande M，Kalagnanam J，Lee H S，et al.The slab－design problem in the steel industry［J］.Interface，2004，34（3）：215.

［8］ Stawowy A.Evolutionary based heuristic for bin packing problem［J］.Computer ＆Industrial Engineering，2008，55（2）：465.

［9］ Haouari M，Serairi M.Heuristics for the variable sized binpacking problem［J］.Computer ＆ Operations Research，2009，36（10）：2877.

［10］ Kalagnanam J，Dawande M，Trumbo M，et al.The surplus inventory matching problem in the process industry［J］.Operations Research，2000，48（4）：505.

［11］ Ford L R，Fulkerson D R.Maximal flow through a network［J］.Canadian Journal of Mathematics，1956，8（1）：399.