幕墙竖框最优计算模型及工程实现

许 芳

（沈阳远大铝业工程有限公司，北京 100029）

1 序言

在幕墙设计中，人们会根据建筑幕墙结构的特点，采用与之相适应的结构计算与分析方法。幕墙的立柱是幕墙的“骨架”，如何设计幕墙立柱，选择合理的计算分析方法，是保证幕墙结构安全和提高经济性能的关键环节。

竖框的计算模型主要有以下几种形式：单跨简支梁、双跨简支梁、等跨铰接静定梁和双支点等跨铰接静定梁。本文将探讨幕墙竖框的四种力学计算模型，分析影响竖框计算的因素，提出最优化的计算模型及在工程实现中的注意事项。

用于分析的工程实例为：幕墙中的危险部位处风荷载为1.5kN/m2，计算层间高L=3.6m，竖框承担的分格宽度为B=1.5m。

校核竖框挠度荷载组合如下：q刚度＝Wk×B＝1.56×1.5＝2.34kN/m

校核竖框强度荷载组合如下：q强度＝（1.4×1×Wk＋1.3×0.5×qEy）×B ＝ 3.564kN/m

2 单跨简支梁

竖框支座反力为：RA= RB=ql/2

竖框的中点弯矩最大，最大弯矩为：Mmax=ql2/8

3 双跨简支梁

我们知道，双跨梁的分析已经非常成熟，在此不赘述。设比例因子 λ=L1/L（短跨与全跨之比）。根据分析，双跨简支静定梁主要注意：

（1）短跨与全跨之比λ，从支座反力的角度出发，在构造允许的情况下，建议λ>0.1，慎重选择λ较小的结构型式。

（2）双跨梁的最大弯矩出现在中间支座处，最大弯矩为Mmax=ql2（3λ2-3λ+1）/8，λ的变化范围是0~0.5，随着λ值从小变大，在相同的外部荷载条件下，双跨梁的各项力学参数的最大值（如最大支座反力、最大挠度和最大弯矩）越来越小。当λ=0.5时，Mmax最小，竖框最省料，Mmax=ql2/32。

（3）要综合考虑构造和造价的要求，立柱是否采用双跨梁结构型式。

4 等跨接静定梁

幕墙立柱每层用一处连接件与主体结构连接，每层立柱在连接处向上悬挑一段，上一层立柱下端用插芯连接支承在此悬挑端上，形成等跨铰接静定梁。

4.1 合适的悬挑长度

设竖框跨长l，悬挑长度为a，悬挑长度与跨长l之比为μ=a/l 。

当简支梁的计算不满足规范要求时，可采用等跨铰接静定梁计算模型。在这种情况下第一跨竖框计算长度为l+a，第一跨可采用双支座计算模型。

对竖框模型进行优化，选求最省料的计算模型。所谓优化就是采用不同μ值，使控制点的弯矩接近并达到最优目标（1/15.2qL2）。

计算之初约定第一跨采用双跨计算模型，经过多次验算，得到下面的表1。

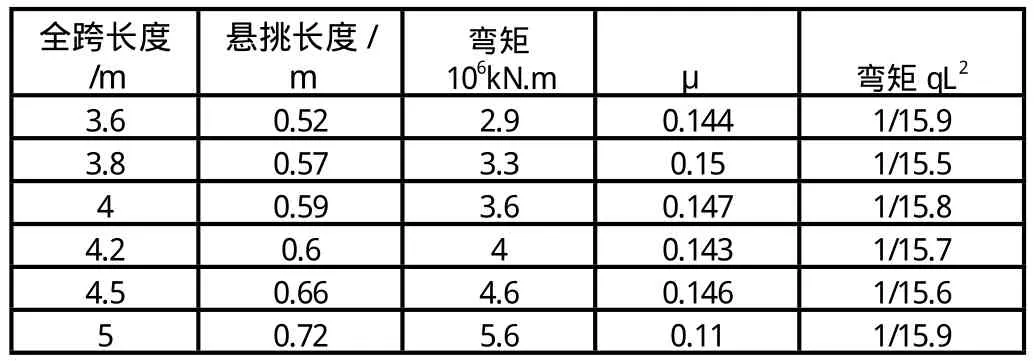
表1

经过多次验算可知，当μ=1/7时，竖框的各支座处的弯矩趋于相等，且接近并达到最优目标。因此建议竖框的悬挑长度与总跨度之比μ=1/7。

通过公式推导也可以得到悬挑长度与总跨度之比μ的最佳值。

第一跨B支座反力：R1B= qL1/2×[1-(a1/L1)2] 第二跨C端集中力：P2= R1B

第i跨C端集中力：Pi= P2×(1- ai/Li)

第 i跨 跨 中 弯 矩：Mi=qLi2/8×[1-(ai/Li)2]2-Piai[1-(1+ai/Li)2/2+ai/Li]

第i跨支座处弯矩：M支=Pi×ai+qai2/2

可知，当支座的弯矩与跨中弯矩相等时，竖框的受力最合理。于是有：

M支=Mi即 Pi×ai+qai2/2=qLi2/8×[1-(ai/Li)2]2- Piai[1-(1+ai/Li)2/2+ai/Li]

可得：ai/Li≈1/6，即竖框的悬挑长度与总跨度之比在μ=1/7。

4.2 最小的计算跨数

最小的计算跨数可以快捷的判别工程中能否采用等跨铰接静定梁计算模型，可以快捷把计算结果推广到符合要求的工程单元中。

采用上面的例子，分别计算3跨、5跨、7跨，判别计算所需的最小跨数。计算之初约定：

（1）最后一跨采用简支梁带悬挑计算。

（2）竖框悬挑长度按照悬挑长度为550mm计算。

分别取3跨、5跨、7跨的竖框，计算各自的变形、弯矩和支座反力，得到表2数据。

表2 3跨、5跨、7跨的变形对比

5跨模型与7跨模型边跨中挠度几乎完全相等，只有0.04mm的差别。5跨模型与7跨模型中跨中挠度只差0.11mm的差别。但3跨模型与5、7跨模型挠度都有非常明显的差别，见表3。

表3 3跨、5跨、7跨的弯矩(107kN·m)对比

从两端看，5跨、7跨模型对应支座的弯矩完全相等。3跨与5跨及7跨模型对应支座的弯矩不相等。表4中从两端看，5跨、7跨模型对应支座的支座反力完全相等。3跨、5跨及7跨模型对应支座的支座反力不相等。

表4 3跨、5跨、7跨的支座反力（KN）对比

因此，从上面的对比中可以得出，5跨模型可以用于7跨及任意多跨，即等跨铰接静定梁的最小跨数为5跨。

5 双支点等跨接静定梁

幕墙立柱每层有两处连接件与主体结构相连，每层立柱在楼层处连接点向上悬挑一段，上一跨立柱下端用插芯连接支承在悬挑端上，形成双支点铰接等跨梁。

5.1 合适的短跨及悬挑长度

设竖框总跨长l，短跨长l1，悬挑长度为a，短跨与全跨之比为λ=L1/L，悬挑与全跨之比为μ= a/L。双跨简支梁的分析依然适用于双支点铰接静定梁。

在双支点的计算中，调整λ和μ的取值，使两个支座的弯矩趋于相等，使控制点的效应接近并达到最优目标（1/15.2qL2）。在实际工程中根据结构的实际情况，我们只能在最优化的计算模型中寻求最合适工程实际的计算模型。

根据上面的例题，经过多次验算，得到下面的表5。

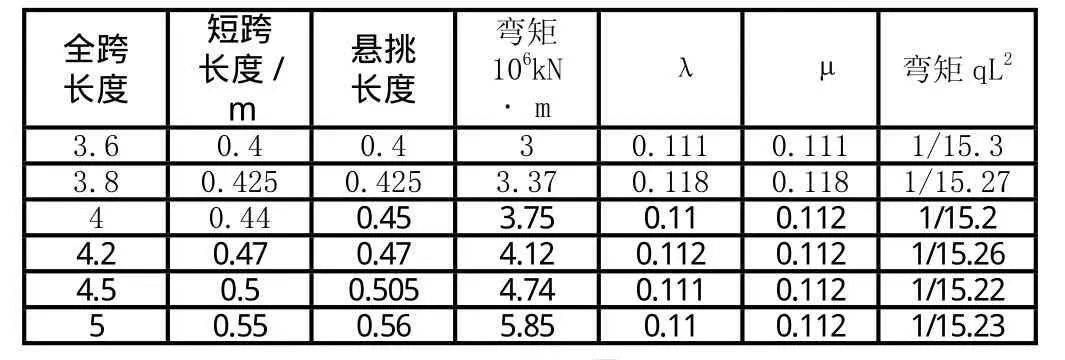
表5

对于上面的数据，所求的弯矩是最优的，而不是最小的。根据上表可以得出：

当λ=L1/L=1/9，μ=a/L=1/9时，双支点等跨铰接静定梁得到最优的弯矩1/15.2qL2。

5.2 最小的计算跨数

采用上面的例子，分别计算3跨、5跨、7跨，判别计算所需的最小跨数。根据上面的例子，层间高为3.6m，短跨为400mm，悬挑400mm。

3跨、5跨、7跨的变形对比见表6。

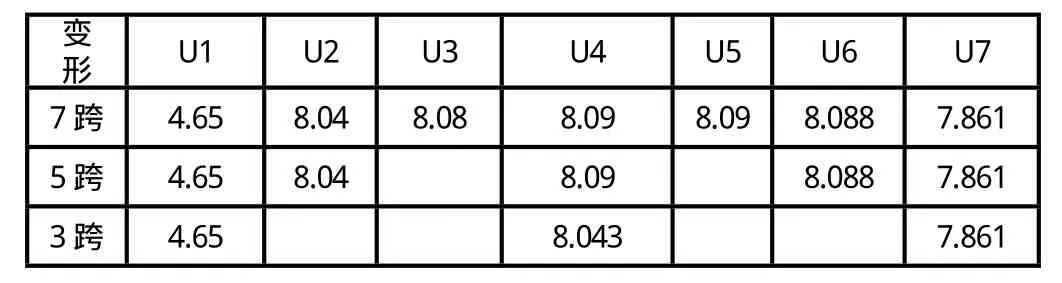
表6

5跨模型与7跨模型中挠度完全相等。3跨模型与5跨模型中跨中挠度只有0.047mm的差别，占0.047/8.09=0.58%，可以忽略不计。

3跨、5跨、7跨的弯矩(107kN.m)对比见表7。

表7

从弯矩对比表中可以看出：从两端看，3跨、5跨及7跨模型对应支座的弯矩完全相等。

3跨、5跨、7跨的支座反力（kN）对比见表8。

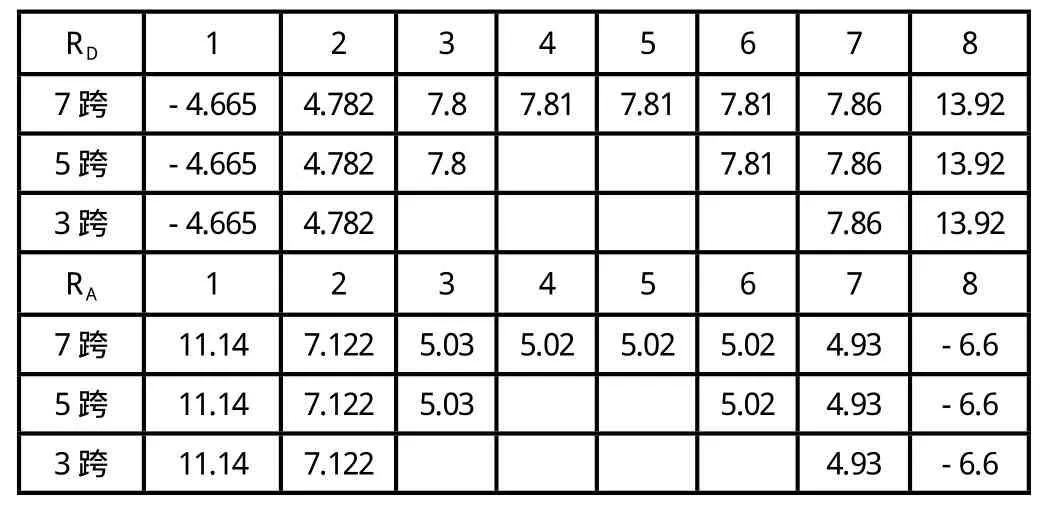
表8

从两端看，3跨、5跨及7跨模型对应支座的支座反力完全相等。

从上面的对比中可以得出，用3跨模型计算结构可以用于5跨及任意多跨。双支点等跨铰接静定梁的最小跨数为3跨。

6 本文总结

四种计算模型各有优缺点，要综合考虑各种因素选择适合的计算模型，不能一概而论。

等跨铰接静定梁每层只有一个固定点，其连接构造最少，经济效益最明显，工作效率最高。但是计算跨度不能小于5跨。而且在一些工程中，由于竖框的型材截面一定，在结构允许的条件下，只能采取双跨梁设计。

要综合考虑构造和造价的要求，立柱是否采用哪种结构型式，一方面要考虑构造是否允许，另一方面还要综合考工程造价和结构安全等因素。例如双跨梁可以改善幕墙立柱的受力，特别是可大大降低立柱的变形，增加立柱的强度的刚度，节约幕墙立柱的材料，但会增加结构的复杂度和工程量。

在工程中，对于大层间单跨简支梁，可以通过增加支座的方式变为双跨简支梁模型。

如图1，吊顶竖框可以在顶梁上增加斜撑，竖框就变为双跨简支梁。

如图2，梁的高度小于设定的支点间距离，在梁底做加强转接件，使竖框变为双跨简支梁。

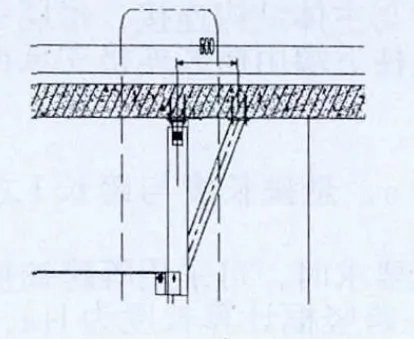
图1

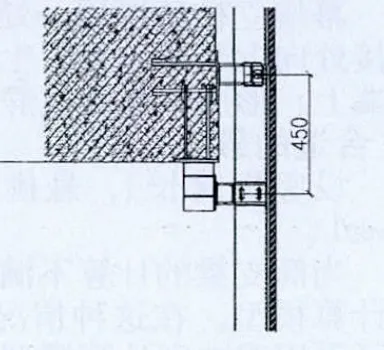
图2

[1] 玻璃幕墙工程技术规范.JGJ 102-2003.

[2] 铝合金结构设计规范.GB50429-2007.

[3] 建筑结构静力手册.（第二版）.