数值模拟中对标储量的确定方法

董梅云 （中石油大庆油田有限责任公司第四采油厂地质大队，黑龙江大庆163511）

1 储量计算方法对比

1.1 常规储量计算法

目前，各大油田地质储量通常采用容积法，计算公式［1］如下：

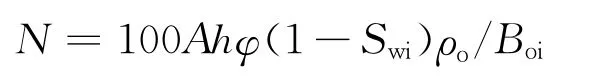
式中，N为石油地质储量，104t；A为区域含油面积，km2；h为平均厚度，m；φ为平均有效孔隙度，%；Swi为平均油层原始含水饱和度，%；ρo为平均地面原油密度，g／cm3；Boi为平均原始原油体积系数。

具体应用时根据区块地质认识程度可对各参数采取不同计算方法。下面以某一区块为例利用容积法计算地质储量。

1）参数标定 根据该区13口密闭取心井物性参数资料，结合电测解释结果和生产动态数据，利用现有井网资料确定了合理的地质储量参数。平面上，以目前实际采用的动态区块为单元，分纯油区和过渡带；在纵向上，以区块内目前划分的单砂层为基本单元；在单砂层内按照沉积微相类型分别确定储量参数，并按不同厚度区间和微相类型分别计算储量。沉积微相类型划分为河道砂 （有效厚度≥1.5m）、主体薄层砂 （有效厚度≥0.5m）、非主体薄层砂 （有效厚度＜0.5m）和表外储层。

2）单井控制面积确定 采用Delauny三角形剖分法对区域进行剖分构成三角形网格后，根据三角形内部每个井点的砂体类型，采用 “井距之半”的理想方法来确定砂体边界，即认为2个不同类型的砂体相互接触，其变化点在2个砂体的中点。

3）计算公式 表内层地质储量和表外层地质储量计算公式［2］如下：

表内层地质储量＝面积×厚度×单储系数

表外层地质储量＝面积×厚度×单储系数× （1－岩性夹层比例－油迹比例）

1.2 数值模拟储量计算法

数值模拟运算的实现，是建立在地质建模的基础上，通过网格的组合，实现地质模型的精细刻画。数值模拟计算的储量，实际上为各网格储量的总和。因此，地质建模是赋予网格属性，最终输出网格储量的过程。

地质建模的基础是构造建模。确定区块范围后，通过三维骨架剖分建立网格模型 （根据区块实际面积大小，通常平面上网格步长在20～40m之间，纵向上按照沉积单元划分）；建立构造模型后，将井点参数离散到所在网格，得到井点网格属性，通过井间插值建立沉积相模型，在其约束下生成网格属性模型；最后经过模型粗化，输出建模储量。

在地质建模结束后，网格数量n、单个网格的平面面积A0、有效厚度h、孔隙度φ、原始含水饱和度Swi已经确定，在已知地面原油密度ρo、平均原始原油体积系数Boi的基础上，根据容积法公式得到区块的地质储量：

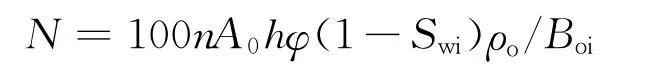
因此，地质建模过程中的井点网格参数选取决定了各单元、各微相储量大小，从而影响数值模拟整体储量。

2 井点参数差异分析及对标储量的确定

2.1 井点参数差异分析

建模过程中根据单井电测解释结果确定井点有效厚度h、孔隙度φ，原始含水饱和度Swi离散到相应网格。通过对全区12521口井电测解释结果参数进行统计，得出计算差值。

1）含油面积 建模区块范围是根据实际含油面积划取，平面上剖分网格后，求得区块含油面积与网格面积一致，无差异。

2）地面原油密度ρo、平均原始原油体积系数Boi地面原油密度ρo、平均原始原油体积系数Boi选用同一套参数，无差异。

3）有效厚度 建模有效厚度h的选取与常规储量方法一致，无差异。

4）孔隙度、原始含油饱和度 ①表内储量计算上，常规储量方法以单砂层为基本单元，在单砂层内按照沉积微相类型分别确定参数；建模中选取各单元电测解释结果参数，若小层参数无解释结果，则应用新方法参数进行赋值，因此两者存在差异。从孔隙度、平均含油饱和度数据 （见表1和见表2）对比来看，建模参数比取心井标定参数在纯油区高10%左右，在过渡带地区高15%以上。②由于表外储量参数选取相同，两者计算储量一致。

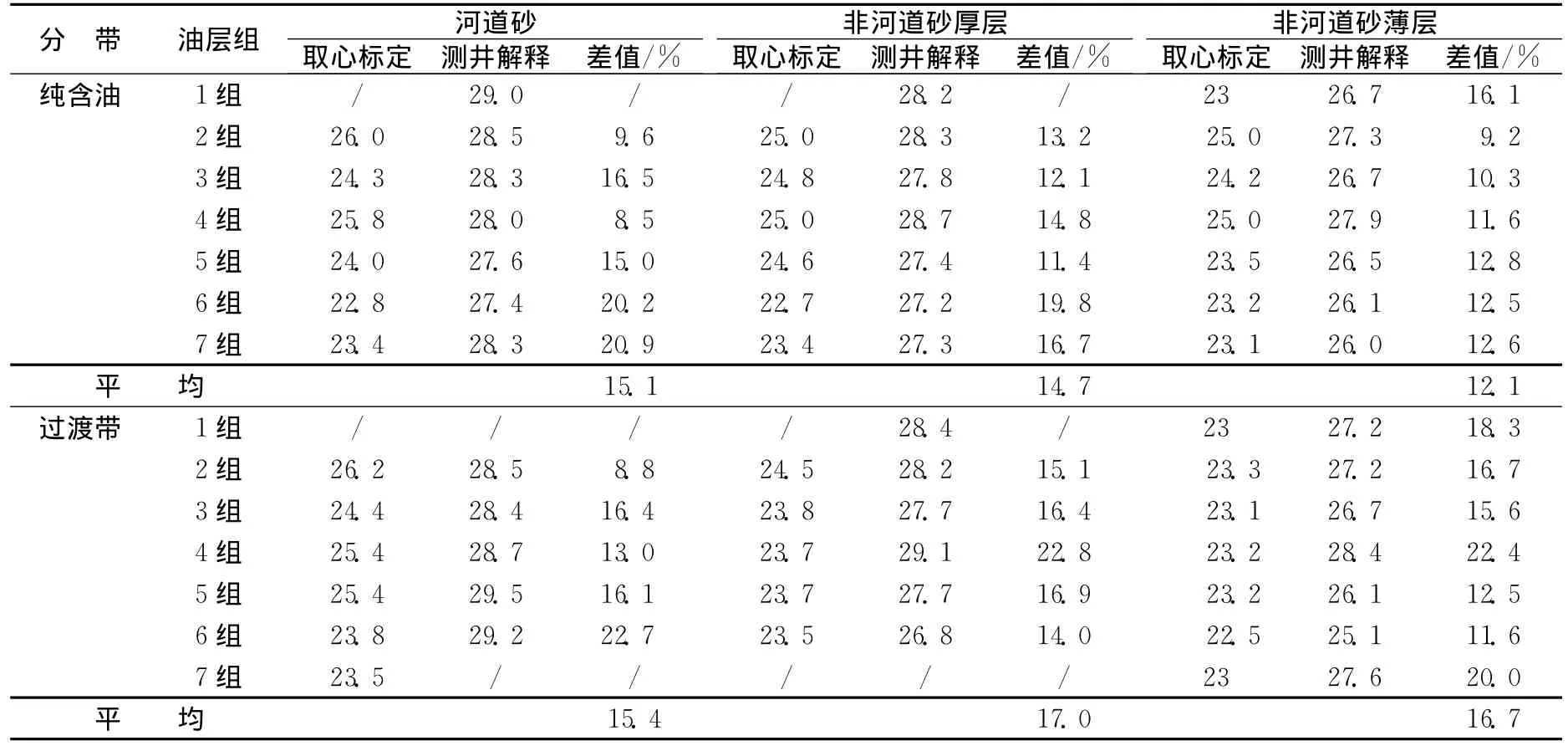
表1 某区各油层组取心标定、电测解释平均孔隙度参数对比表

2.2 对标储量的确定

通过对井点电测解释参数的统计分析，确定了地质建模中全区不同油层组、不同微相的平均孔隙度和原始含油饱和度，与取心井标定参数存在差异，导致数值模拟表内储量偏大，因此数值模拟对标储量不能直接选用常规计算的储量。同时针对各区块砂体发育状况的不同，对标储量也不能确定为同一平均值，应结合区块情况具体分析。

综合考虑各项因素，完善了数值模拟中对标储量的确定方法：①首先统计研究区块单井分油层组、分微相的平均孔隙度φx1和原始含油饱和度Soix1；②已知取心井分油层组、分微相标定的平均孔隙度，原始含油饱和度Soix2，根据公式计算电测解释参数计算储量与取心井标定参数计算储量的比值；③在利用取心井标定参数计算储量过程中表内储量的基础上乘以Ax系数，得到分油层组、分微相的表内对标储量；④用表内对标储量与表外储量相加，得到分油层组、分微相的对标储量，在±5%范围内确定为合理值。

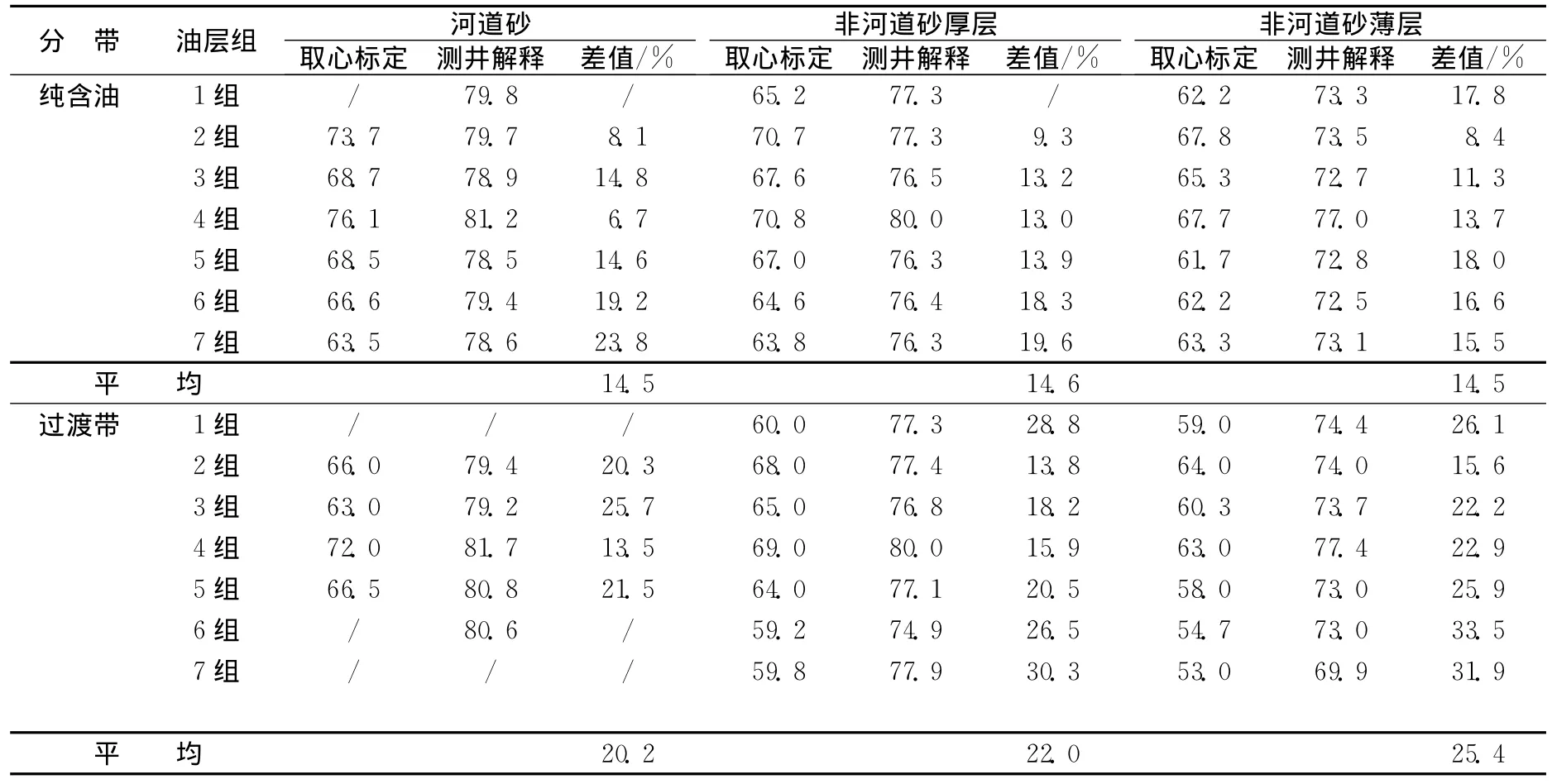
表2 某区各油层组取心标定、电测解释平均含油饱和度对比表

3 对标储量的精度验证

选取某区某块模型对数值模拟对标储量进行验证，模拟区块面积5.97km2，平面网格大小为35m×25m，纵向上划分96个层，共有网格数921600个。参与建模井数679口井，基础井49口，一次井56口，二次井121口，三次井219口，其余为聚驱井及三元井。建模参数应用井点电测解释结果，得到区块平均建模参数 （见表3和见表4）。

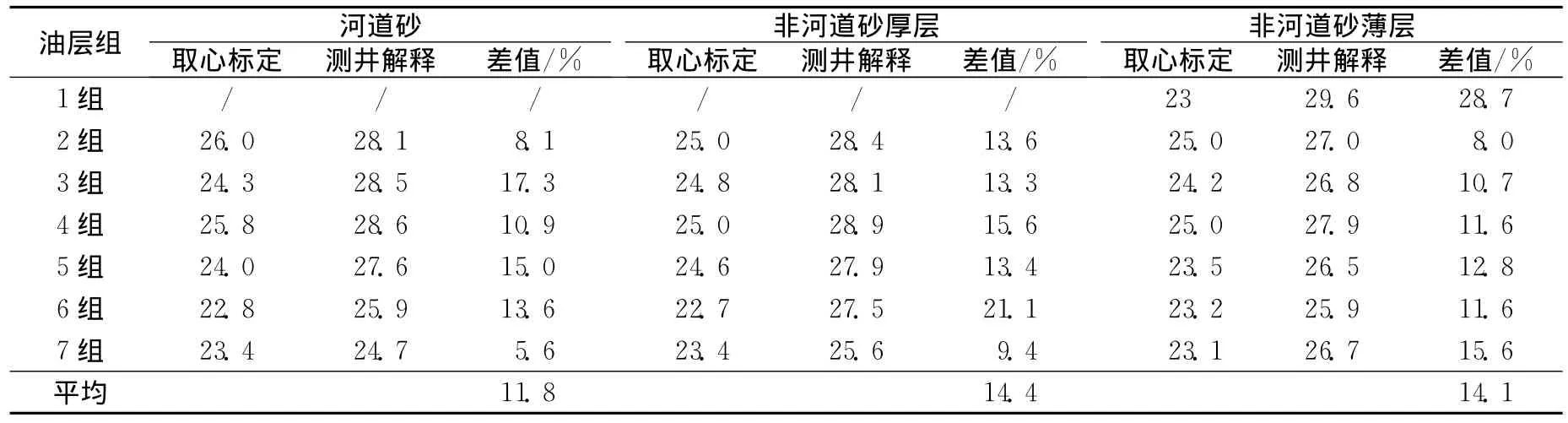
表3 某区某块各油层组新方法、建模平均孔隙度对比表

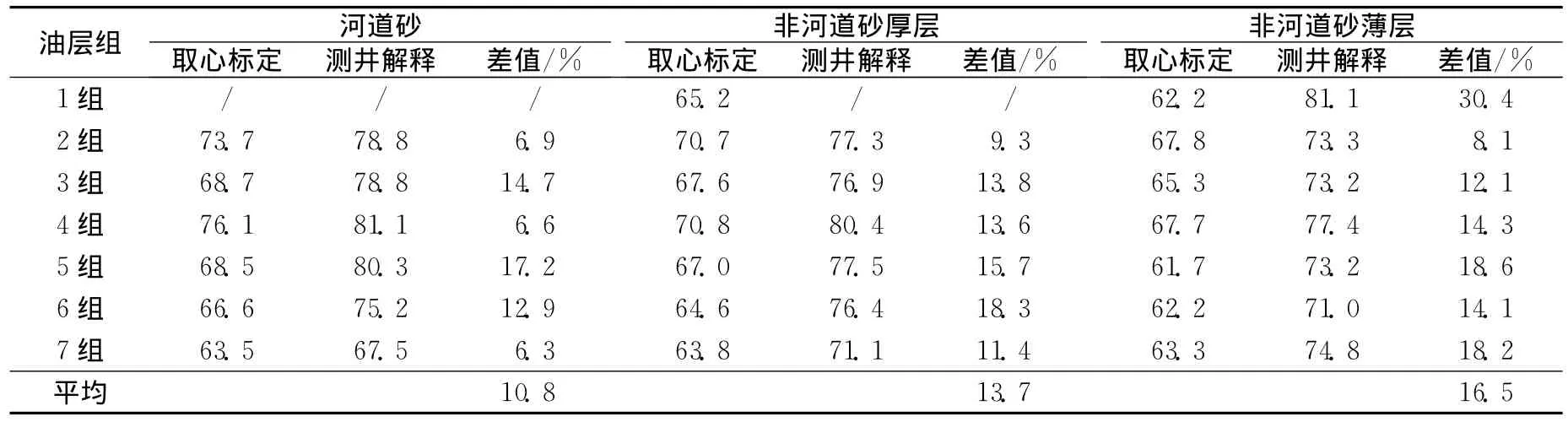
表4 某区某块各油层组新方法、建模平均含油饱和度对比表

应用对标储量确定方法，计算区块的对标储量，得到区块各油层组之间储量差异范围 （见表5）。

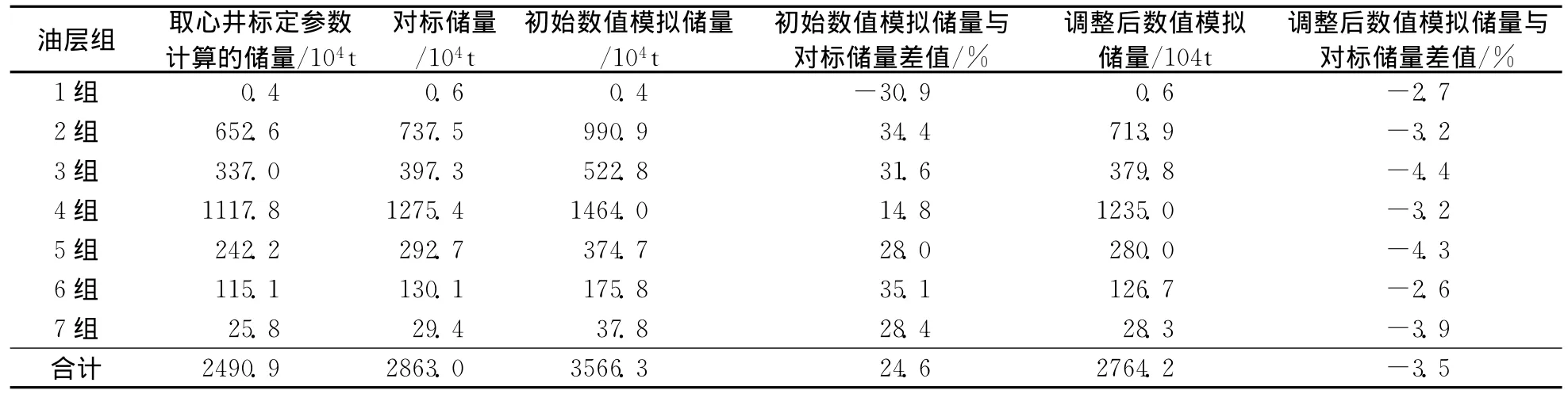
表5 某区某块数值模拟储量差值对比表

经过分析，确定井间插值的误差造成了模型初始储量偏大。重新修正地质模型，若拟合取心井标定参数计算的储量，则储量偏小，后期含水偏高；将模型储量调整为对标储量误差范围内，储量正常，含水拟合效果较好 （见图1）。

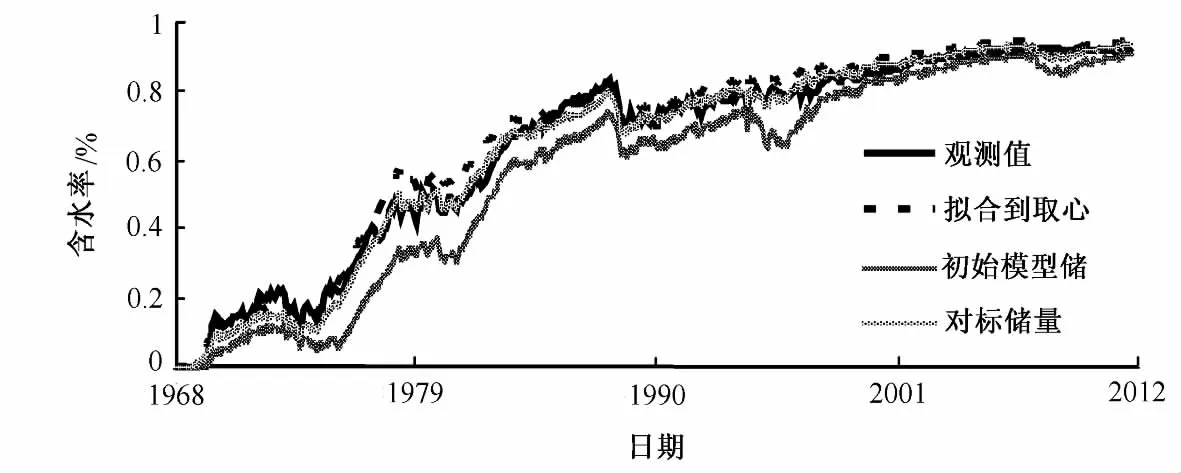
图1 含水拟合情况

4 结 论

（1）通过对全区井电测解释结果的统计分析，确定了建模储量与取心井标定参数计算储量产生差异的主要原因为井点孔隙度、原始含油饱和度参数选取不同，完善了数值模拟对标储量的确定方法。

（2）针对地质建模储量超出对标储量误差范围的情况，应检查建模选用参数，同时参考初次含水拟合情况，对不确定性参数进行调整，修正地质模型，为精细历史拟合奠定基础。