用光线追迹方法仿真菲涅尔双棱镜干涉实验
2013-12-01崔秀芝
董 键,崔秀芝
(曲阜师范大学 物理工程学院,山东 曲阜273165)
1 引 言
菲涅尔双棱镜干涉实验是演示分波面干涉原理的基本实验之一,是传统实验项目[1-6].该实验测量光波波长的精度不高[7],其原因主要是对该实验理论上认识不完善,对于光线如何在光路内传播,没有完整的理论公式表达.因为该实验主要的关注对象是干涉现象并用该现象测量波长,因此,基本的关注点应该是光程和波振幅,本文在研究过程中发现,寻求光程和波振幅的答案,都可以用光线追迹的方法来解决,在此基础上笔者提出了一种测量光波波长的方法,用来提高该实验的精度.
2 菲涅尔双棱镜实验的基本原理
菲涅尔双棱镜实验的基本装置见图1,激光器发出平行光,经过扩束镜变成从坐标系原点O发出的发散光束,透过光阑进入菲涅尔双棱镜(以下简称“棱镜”,它被x轴平分为上下两对称部分,这两部分分别简称为“上棱镜”和“下棱镜”),光线经棱镜折射,到达测微目镜的分划板(光屏),来自上下棱镜的折射光线在分划板上叠加,形成干涉条纹,可以在目镜中观察,并能测量干涉平面上的有关长度.图1为装置俯视图,棱镜的棱脊垂直于纸面,棱镜底面垂直于x轴,棱脊可以迎着入射光,也可以背着入射光(图中显示后者).在目镜分划板上,干涉条纹垂直于纸面,并沿着y方向周期性扩展.做好该实验需要调节各个光学器件在光具座上共轴、中心等高.

图1 菲涅尔双棱镜实验装置示意图
根据实验原理[8],点光源O经过棱镜之后将形成2个虚像O1和O2(又称为虚光源),相距为d,虚像面到目镜分划板的距离为L,若光波长为λ,干涉条纹的间距为δ,则

式(1)是讨论该实验的基本依据.
3 光线追迹基本原理
对于由若干界面分割的光学介质系统,2个界面之间充满了均匀介质,对这样的系统,光线追迹的基本依据是光的折射定律:
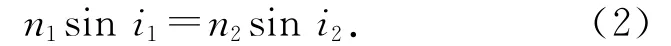
根据该定律,可以由入射光线的方向求出折射光线的方向,方法是将该定律矢量化[9].令q是光线方向的单位矢量,n是光线所在均匀介质的折射率,定义矢量k=nq,再令相邻2种介质界面的单位法矢量为Ω,则可以证明:

这是光线从介质1进入介质2时两者传播方向之间的关系.至于界面的法矢量Ω,则可以根据界面方程f(x,y,z)=0用下式计算:

其中,▽f是函数f的梯度,|▽f|是梯度的模.
根据式(3)和(4),可以计算任何光线的传播路径,并计算它们在光屏上的落点,进而依据下式求出光线的光程φ:

其中lj是在介质j内光线路径的长度.
另外,根据光源的性质,可以计算光经过介质之后在光屏上振幅A(y)的分布(见后),然后根据相干叠加的公式计算2束光干涉强度分布I(y):I(y)=+2A1A2cos[2π(φ1-φ2)/λ],(6)其中光程φ1和φ2也是y的函数.
4 用光线追迹法仿真光线分布
首先计算从点光源O发出的光经棱镜折射后的分布,以便为后续讨论奠定基础.
模拟计算使用软件Mathematica,计算中的棱镜参量如下:折射率n=1.52,楔角α=1°,棱镜厚度L2=3mm.其他参量是:原点O到棱镜底面的距离L1=50mm,棱脊到分划板的距离L3=300mm.
图2是用光线追迹方法计算出的不同发散角的光线到达分划板的光路情况,从O点以发散角φ=0(极限意义)出射的光线经折射后在分划板上被照亮的位置,经过上下棱镜后分别向对方区域偏折(偏折都是从棱镜的棱脊开始的),因而合成区域有交叠,形成干涉区,这个区域是可以计算的;在交叠区之外,是未交叠区,不形成干涉.计算该图所对应的发散角φ=-2°~2°,可见,形成干涉只需要很小的发散角.
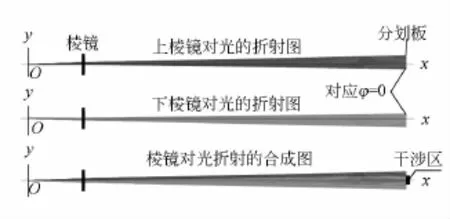
图2 棱镜对光的折射仿真图
5 光线在分划板上的光程分布
在光线追迹的基础上,很容易计算来自上下棱镜的光线在分划板上的光程分布,见图3(a),其中曲线φ1表示来自上棱镜的光程分布,曲线φ2表示来自下棱镜的光程分布.可见,无论来自棱镜哪一部分的光线,其光程都不是常量,除了在y=0处2条光线的光程相等,其他处的光程都不相等,因而有了光程差Δφ=φ1-φ2,光程差的分布见图3(b),该图显示,光程差是线性分布的.光程差的存在,是形成干涉的必要条件.
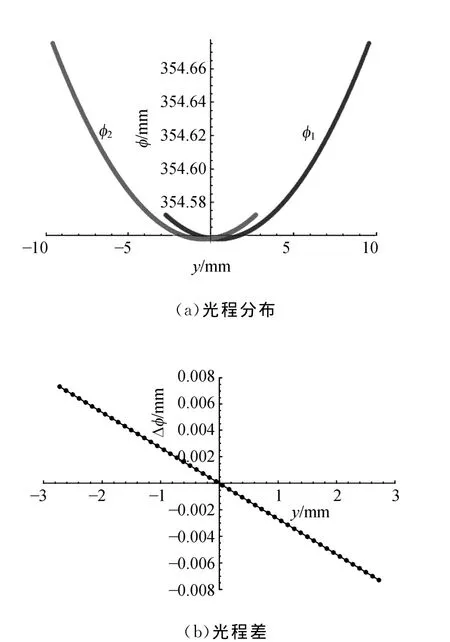
图3 来自棱镜上下部分的光线在分划板上的光程分布及光程差
6 关于虚光源
“虚光源”是菲涅尔双棱镜干涉实验的重要概念,其含义是:从光源O发出的光线被上棱镜折射之后,光线的反向延长线将交于点O1,形成上虚像;光线被下棱镜折射后形成下虚像O2.这样从O点发出的所有光线,就等效于从这2个虚像发出,好像棱镜并不存在[10].基于该认识,菲涅尔双棱镜干涉实验被等效于2个相干点光源O1和O2所发出光的干涉,就可以套用杨氏双光源干涉实验的计算公式[式(1)].
用光线追迹方法计算被棱镜所折射光线的反向延长线,见图4(a),来自上下棱镜的反向延长线分别汇聚于位置O1和O2,这2个位置在点光源O的右侧,与y轴相距δL.粗略看,延长线似乎分别相交于一点,但如果把O1附近区域放大,则如图4(b)所示,延长线并不相交于一点,而是形成有一定宽度的“细腰”.因此,严格来讲,虚光源O1和O2并非点光源,使用点光源概念来进行干涉计算会对式(1)造成一定的误差.对“细腰”的宽度进行考察,以判断其具体粗细.方法是寻找“细腰”最细的位置界面,计算每条延长线与该界面交点的y值并乘以2,作为两虚光源的间距d,这样可以得到d的分布曲线,见图5(a),从该曲线上可大致得出d=0.943 2~0.943 9mm,“细腰”的宽度为0.7μm,远小于人眼的分辨能力,对于该实验的测量精度,可以将O1和O2当做点光源来看待.

图4 虚光源及局部放大图
因为“细腰”可以当做点光源,所以,通过“细腰”O1和O2的任何2条光线反向延长线之间的距离都可以作为2个虚光源的间距d.选择2条水平延长线之间的距离作为d,确定d的具体做法见图5(b),该图是经过上棱镜折射光线的斜率k与光线在分划板上位置y的关系曲线,是直线,该直线与y轴的交点对应k=0,相应的y值乘以2作为d.

图5 虚光源间距d随着发散角φ的分布和确定虚光源间距的方法
关于虚光源的性质,还可以考察其间距d和虚像所在平面的位置δL随棱镜位置L1的变化关系,见图6,可见两者的关系都是线性的.要注意的是,δL随L1变化很小,可以近似认为虚像面的位置是不变的.

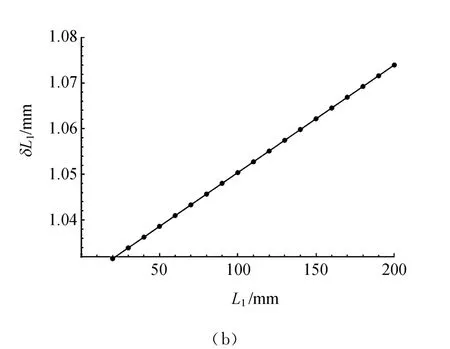
图6 虚光源间距d和虚像面的位置δL随棱镜位置L1的变化
7 式(1)的模拟证明
有了图3光程差的结果,可以计算分划板上干涉光的强度分布,因为光程差是线性的,所以光强随y的分布是周期性的(见后),其周期就是干涉条纹的间距δ.根据式(1),在光的波长λ已知和虚像面到分划板的距离L固定的情况下,δ与d成反比,二者的乘积等于λL.模拟计算λ=0.6μm和L+δL=300mm情况下δ与d的关系,见图7,经过拟合,证明二者符合反比关系,比例系数为0.179 373,容易验证,该数值非常接近λL,证明式(1)的近似程度很好,也证明虚光源概念的引入是合理的.
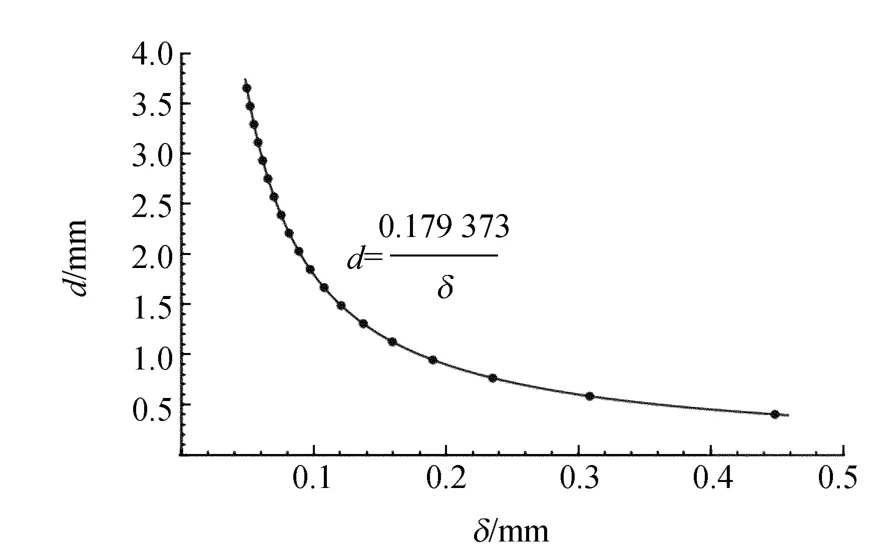
图7 虚光源间距与条纹间距的模拟关系
8 凸透镜使虚光源成像
二次成像法要在棱镜与分划板之间加1个凸透镜,使2个虚光源成像于分划板.图8模拟了该过程,所使用的凸透镜焦距为64.5mm,左极点与棱镜的棱脊相距30mm.图8(a)表明,上下棱镜的折射光经过凸透镜后汇聚的位置是颠倒的,其位置用箭头指示;将该位置附近区域放大,即为图8(b),它表明光线也并非汇聚成一个点,而是汇聚成“细腰”,这在透镜有球差的情况下是可以预料的.不过,该图真正的含义在于:“细腰”在x方向扩展范围很大,在此范围内,像宽都差不多,因而很难准确判定像的位置,这正是二次成像法测量光波波长误差大的原因所在.
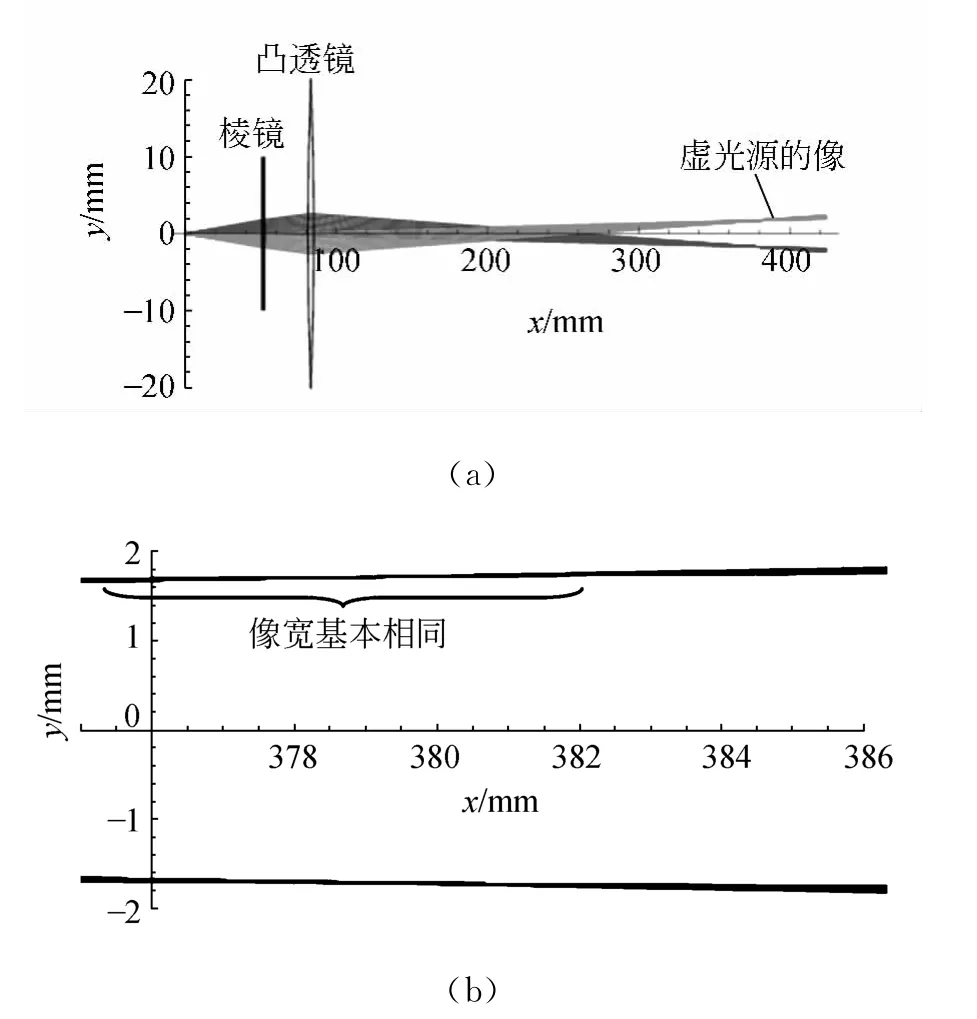
图8 加凸透镜所成虚光源的像及其局部放大图
9 测量光波波长的方法
通过光线追迹清楚该实验的细节后,作者提出了测量光波波长的方法,该方法可以提高波长测量的精度,而且不需要知道棱镜的具体参量.下面是该方法的原理.
根据虚光源的性质,可以得到
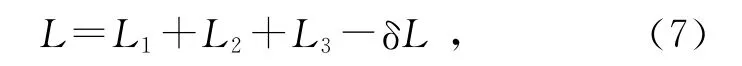
根据经验,式(7)中右边的长度量很难测定,直接测量会引起L较大的误差,尤其是在使用激光光源的情况下,O点的位置难以确定.把式(1)和(7)结合起来,得到
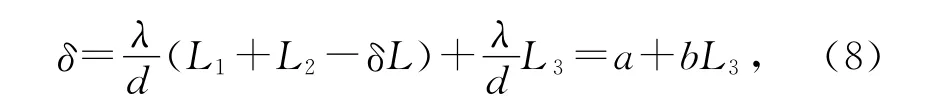
虚光源的间距d只与L1有关,在固定L1的情况下,改变L3,就可以测量出不同的δ,从而构成δ-L3的线性关系,通过拟合得到系数b,

这样得到的b具有L3的测量精度,因为光具座上的毫米刻度尺可以测量出4位有效数字.虽然L3并不能代表分划板的位置,但因为可以把这一固定的偏差归于截距a中,所以测量精度得以保证.于是对应某个L1的距离L就以较高的精度被计算出来,

为了测量2个虚光源的间距d,需要测量分划板上干涉区的y向宽度w,这在使用激光光源的情况下可以得到较高的精度.因为仿真研究表明,干涉条纹的间距δ与L1有关,L1越大,δ越小,二者是反比关系.因此,实验时取较大的L1,让δ尽可能地小,干涉条纹尽可能地细,这样,干涉区内就容纳了足够多的条纹,其边界比较容易确定.在此条件下,可以测量光线经过棱镜的最大偏折角tanβ,原理见图9.图中,保持光屏位置不变,棱脊的位置为x1,相应干涉区宽度为w1;移动棱镜,使棱脊的位置变为x2,干涉区宽度相应变为w2,则有如下关系:

虽然棱脊的绝对位置很难测定,但位置的差值x2-x1却具有光具座刻度尺的测量精度,而w2-w1具有测微目镜的测量精度,所以tanβ的测量精度得到提高,

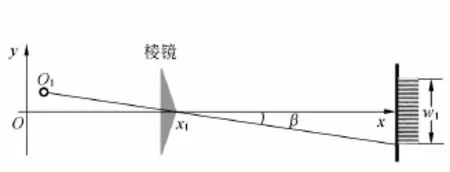
图9 测量光线最大偏折角tanβ
在测量了tanβ之后,根据如下关系计算虚光源的间距d,

于是,光波的波长为
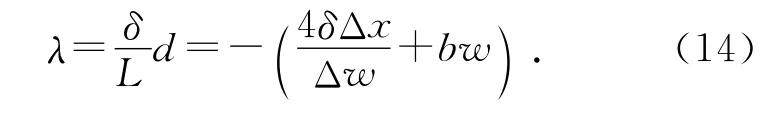
为了充分利用分划板的有效宽度(通常为8mm),适当地调整L3,使干涉区宽度接近有效宽度.
10 关于折射光在分划板上的振幅分布
根据式(6),要计算干涉光强,就需要知道来自2条光线的振幅A1(y)和A2(y),这在光源性质已知的情况下是可以计算出来的.假定激光器输出的光束横截面上光强分布均匀,则通过光线追迹可以证明两点(证明过程从略):
1)激光经过球面扩束镜之后光能是各向同性发散的;
2)经过棱镜之后光线在分划板上的位置y与光线的发散角φ成线性关系.
这2点结合起来,就得到如下结论:
在忽略光线与分划板之间的夹角与直角有微小偏离的条件下,折射光的振幅和强度都是均匀分布的,即A1(y)=A2(y)=A0.于是,
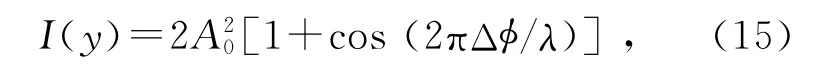
相位差Δφ的分布见图3(b),它是线性分布的,因而强度I(y)在分划板上是周期性分布的,相邻2条亮纹之间的间距δ相同.
11 结束语
菲涅尔双棱镜干涉实验能够用光线追迹方法进行全面仿真,由此可以深入全面地了解该实验的细节,结论直观可靠,并在此基础上提出了光波波长测量的方法,提高了测量精度,而且不需要知道棱镜的具体参量(例如折射率、楔角和厚度),对做好该实验很有启发性.
[1]金重.费涅耳双棱镜实验精度的提高[J].河北大学学报,1981(1):89-90.
[2]秦庚生,侯永忠.菲涅尔双棱镜干涉实验的改进[J].物理实验,1987,17(2):67-69.
[3]张国英,徐克耀.用双棱镜“等位移法”测光波波长[J].首都师大学报,1997,18(1):45-48.
[4]周亚俊,王秦镜,马秀芳,等.关于“双棱镜必须均匀照亮”的深入探讨[J].物理实验,2003,23(7):46-48.
[5]廖立新,刘生长,米贤武.用双棱镜测激光波长的简单方法[J].物理实验,2007,27(7):34-35.
[6]葛松华,唐亚明.菲涅耳双棱镜干涉实验中距离参数的研究[J].大学物理,2010,29(4):43-45.
[7]王明吉,张利巍,王晓莉.双棱镜干涉4种实验方法的研究与探讨[J].物理实验,2008,28(4):25-27.
[8]周殿清.大学物理实验[M].武汉:武汉大学出版社 ,2005:260-265.
[9]张以谟.应用光学[M].北京:机械工业出版社,1982:6-7.
[10]袁成卫,刘廷贤,张海新.费涅耳双棱镜干涉实验中的“虚光源”[J].物理实验,1999,19(3):48-49.
