激光散斑照相法测量压电陶瓷管的电压响应位移特性

2013-12-01王中平张增明孙腊珍

物理实验 2013年3期

王中平，张权，朱玲，张增明，孙腊珍

（中国科学技术大学物理学院物理实验教学中心，安徽合肥230026）

1 引言

压电陶瓷是微位移驱动、微制动的主要元件，在精密测量和现代科学研究仪器中起着非常重要的作用.压电陶瓷微驱动器是利用逆压电效应制作的新型固态执行元件，其具有体积小、驱动电压低、位移量大、可集成化等特点，在精密光学、微型机械、微电子技术等高新技术领域取得了广泛地应用，如扫描探针显微镜中的扫描器部件与微位移样品选择台.科学家们通过对压电陶瓷的电压响应的位移特性进行研究，使得在器件的小型化、微型化以及器件的蠕变性能等方面获得了很大的改善［1-2］.

研究测量压电陶瓷电压响应位移特性的方法有干涉条纹法、光杠杆法等.一般测量压电陶瓷的压电与位移关系采用光学相干法，这种方式需要搭建稳定的干涉光路，调试操作困难，并且后期数据处理过程相当繁琐，同时干涉条纹的质量也影响测量的精度［3-6］，对本科生的教学实验而言实验难度太大.而单光束激光散斑技术测量位移的光路简单，成本低，调试操作方便，数据处理方便，本文结合CCD辅助的激光散斑技术可以测定压电陶瓷管的伸缩量与电压的关系及其回滞效应，具有直观、快速、精确的优点，适合开展本科生的教学实验.

2 实验原理

激光散斑微小位移测量的基本原理见文献［7］.图1为实验原理图，O1X1轴位于毛玻璃的粗糙表面上，O2X2轴位于观察平面（CCD探测器表面）上.由激光器出射的光束为高斯光束，实验中透镜可以改变光束的发散角，但根据高斯光束的传播理论推断，在近轴区激光高斯光束经凸透镜后仍为高斯光束，但束腰位置和尺寸大小会发生变化［8］.经过凸透镜的激光光束沿光轴O0O1O2方向入射到毛玻璃的面上，假定其光束束腰位置在O0处，从O0到O1的距离等于P1，从O1到O2的距离为P2.对自相关函数归一化处理可以求出散斑的平均半径.而散斑统计平均半径由理论公式（1）进行计算：

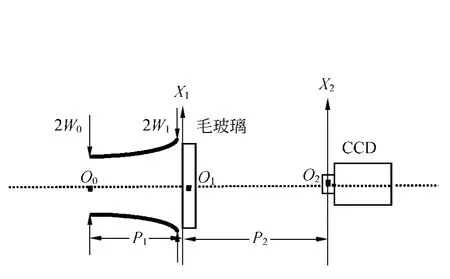
图1 激光散斑的实验原理图

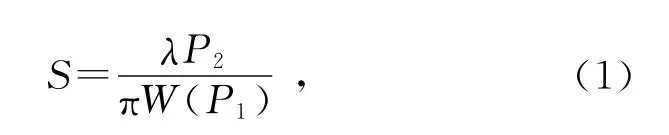
式中W（P1）为照射到毛玻璃的光束的半高半宽，可推断激光光束的空间分布性质.姚琨等在研究不同光束照明下散斑的规律时，曾对ρ（P1）和W（P1）对散斑的影响进行了详细讨论［9-15］.可知，当毛玻璃在自身平面内运动时，其散射形成的散斑也会随之发生平移，其平移量ΔX与毛玻璃的平移量d0之间的关系为：

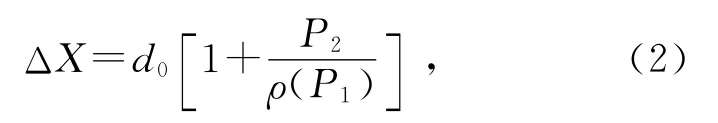
式中ρ（P1）表示照射到毛玻璃表面的高斯光束波阵面的曲率半径.激光散斑斑图的平移量ΔX可以运用归一化的互相关函数关系推导求解，进而得到毛玻璃的面内平移量d0，即压电陶瓷的电压驱动伸缩量.

3 实验装置和方法

实验装置见图2，凸透镜L的焦距为50mm.He-Ne激光器出射的激光束经双偏振器元件对光强进行衰减（以免CCD因曝光量过大而饱和或损伤）后，再经全反射镜反射至凸透镜L，经凸透镜L扩束再照射到叠层型压电陶瓷顶部的毛玻璃上，这样在毛玻璃的后面就可以得到客观散斑场.可通过压电陶瓷驱动电源（哈尔滨溶智纳芯科技有限公司型号：Rhvd1c200v）对压电陶瓷（型号：PTDC200／5×5／18）施加不同的电压，驱动压电陶瓷伸展来移动毛玻璃，使毛玻璃在自身平面内做微小位移.用计算机上的图像采集程序控制CCD摄像机，对物体发生位移前后的散斑图进行采集，CCD像元尺寸为256像元×256像元（CCD像素实际定标校正后1像元＝11.6μm），然后将图像保存在计算机内，通过编写程序对散斑图像进行处理，通过自编写的线性拟合程序计算散斑在平面内的x和y方向的散斑半径，再通过计算求出散斑的统计半径，并计算散斑位移量，即毛玻璃面内位移，也就是压电陶瓷的电压驱动位移量的大小.

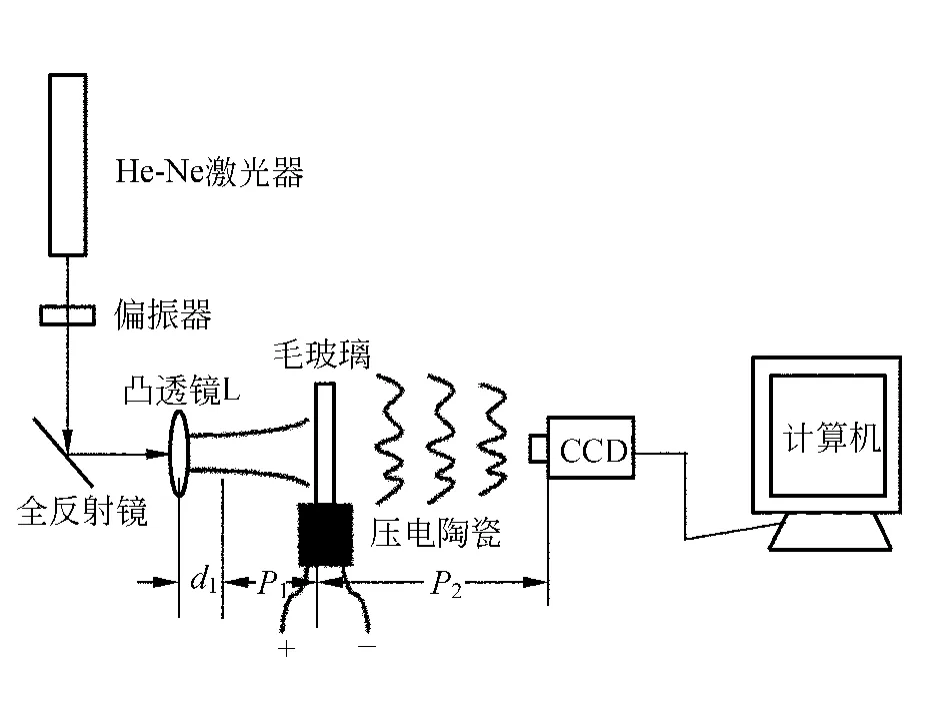
图2 激光散斑法测量压电陶瓷位移特性的实验装置图

4 分析讨论

实验采取固定氦氖激光器的激光出射口到凸透镜的距离（730mm）、凸透镜到毛玻璃的距离（150mm）以及毛玻璃到CCD接收面的距离（450mm），通过对压电陶瓷加载不同的电压改变毛玻璃的微小位移量来研究激光散斑图像的互相关关系确定微小位移的大小.实验中选取毛玻璃到CCD接收面的距离450mm为实验优化参量，随着毛玻璃到CCD接收面的距离逐渐减小，扩束的激光照射到毛玻璃面的扩大，扩束激光的质量为中央清晰明亮，从中心到边缘光强逐渐衰减，CCD的接收面采集的图像同样呈现中央图像清晰，从中央到边缘图像清晰度有所降低，散斑尺寸逐渐变小，清晰度有所降低，但对实验数据处理结果影响很小，在图像进行数据处理时，计算机程序自动选择中央的清晰区域进行分析计算，所以图像边缘效应对测量误差几乎没有影响，可以忽略不计.

通过CCD采集的散斑图像如图3所示，可以直观明晰地分析出散斑半径的尺寸大小.对压电陶瓷施加逐渐升高的电压，待电压稳定后，记录不同电压值对应的激光散斑图像.利用计算机互相关拟合程序，计算每一幅散斑图与零电压时散斑图的互相关关系，可分别得出其散斑图的像素变化大小.再由式（2）计算出不同电压值时毛玻璃的面内位移的微小位移量，即压电陶瓷的电压响应位移值.图4给出了压电陶瓷的不同电压响应位移曲线与线性拟合曲线.可以看出，实验的测量结果与生产厂家提供的位移值基本符合.在0～190V的电压范围内，压电陶瓷随施加电压的变化基本为线性变化，其位移随电压的响应变化率的大小为0.150μm／V（生产厂家的响应变化率的大小为0.148μm／V）.图5给出了压电陶瓷随减载电压的降低，其位移特性的变化曲线.由于逆电压效应的存在，电压位移的响应曲线已经无法满足线性关系.同时也存在滞后现象，主要是电源内阻过大，压电陶瓷放电缓慢，虽然在测量回程中尽量延长了放电时间，但电源引起的误差不可忽略.

图3 特定P2值下的激光散斑图像

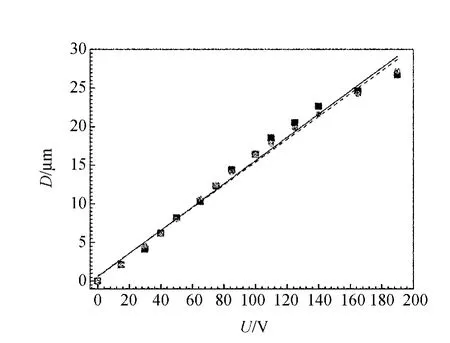
图4 加载不同电压对应的压电陶瓷的位移响应值与拟合曲线（方块对应实验测量值，实心圆对应生产厂家给定值）

本实验采用光学实验平台和磁性表座，利用加载电压驱动毛玻璃在横向上发生微小位移，采取了CCD图像采集技术和计算机图像处理技术对单光束激光散斑实验进行了实验教学研究.相对于原来的干板成像技术来说，避免了全息干板曝光方法中的诸多不便和繁复，以及再现图像的精度不够等缺点，使得实验操作简单，现象直观，易于观察.但在实验中需注意驱动电源的电压稳定性对压电陶瓷造成的影响.同时系统误差主要来自于激光器的起伏，探测器的噪声以及光学平台的稳定性能等方面.本实验同时存在非常大的提升空间，可以鼓励学生利用显微激光散斑相关法以及主观散斑的光路及散斑相关法等不同的研究方法来对压电陶瓷的电压响应位移曲线进行实验研究.

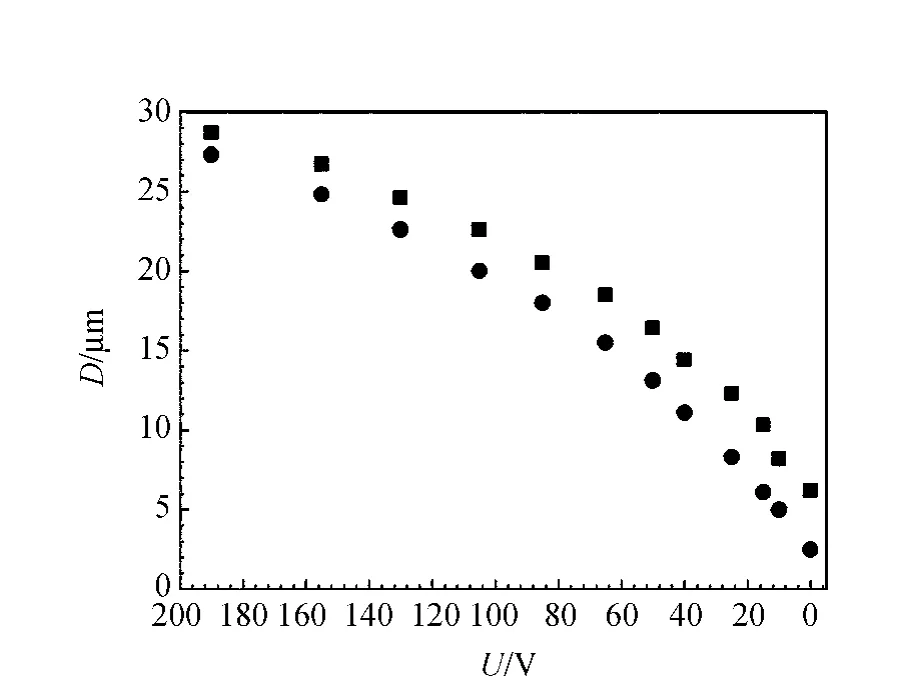
图5 减载不同电压对应的压电陶瓷的位移响应值与拟合曲线（方块与实线对应实验测量值，实心圆与虚线对应生产厂家给定值）

5 结束语

采用CCD辅助激光散斑互相关技术方法研究测量压电陶瓷的压电位移特性并标定其线性区间，该方法测量光路简单，且对系统仪器的装配误差要求低，实现了实验操作的简单化、实验现象的直观化以及现代化新技术在实验教学中的利用.了解压电陶瓷的电压位移响应特性以及逆压电效应的存在对其影响，让学生进一步认知在现代科学仪器中具有非常重要应用价值的压电陶瓷的应用原理与作用机制.现代化的实验教学方法在优化实验教学模式的同时，也拓展了学生的知识层面，使学生在课堂上所学习的理论和实验中观察到的现象有机地结合在一起，激发了学生对实验学习的兴趣和积极性，为学生发挥创造性思维提供了基础.

［1］宋道仁，肖明山.压电效应及其应用［M］.北京：科学普及出版社，1987.

［2］李龙士.美国开发压电陶瓷材料的现状和动态［J］.材料导报，1992，（6）：67-69.

［3］刘培森.散斑统计光学基础［M］.北京：科学出版社，1983：1-50.

［4］丹锑J C.激光斑纹及其有关现象［M］.黄天乐，等译.北京：科学出版社，1981：1-76.

［5］蔡文贵.CCD技术及应用［M］.北京：电子工业出版社，1992：1-98.

［6］刘家恕，李强，朱箭.数字图像处理技术在叠栅条纹测量中的应用［J］.物理实验，2011，31（2）：40-42.

［7］王中平，张权，朱玲，等.CCD成像辅助激光散斑实验［J］.物理实验，2010，30（10）：11-14.

［8］黄水平，郭旭东，张飞雁，等.拟合法测量高斯光束的束腰半径［J］.物理实验，2010，30（3）：29-31.

［9］姚焜，侯碧辉，张增明，等.散斑位移法测量高斯光束的空间分布［J］.强激光与粒子束，2000，12（2）：141-144.

［10］高翔，杨白久，何焰蓝，等.用激光散斑法测盐水溶液浓度的改进［J］.物理实验，2007，27（2）：42-45.

［11］姚焜，陈蝶萍，张权，等.散斑位移量与照明光束特性关系的实验研究［J］.物理实验，2003，12（11）：6-9.

［12］轩植华，霍剑青，姚琨，等.大学物理实验（第三册）［M］.2版.北京：高等教育出版社，2006：14-22.