基于逻辑时序优化的电容测压器采样电路
2013-12-01马铁华李新娥
郭 凯,马铁华,李新娥,王 强
(1.中北大学电子测试技术国家重点实验室,山西 太原 030051;2.仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引言
准确可靠的膛压数据是分析内弹道和装药结构合理性及弹体、引信、身管、炮尾、炮栓和炮架强度和刚度设计的基本依据。而膛压的测量已经逐步从铜柱(铜球)测压法发展到了电容测压法。传统的电容测量电路种类繁多,采用集成芯片PS021为核心的电容式压力测量系统,优点在于测试过程简单,不需要专门设计电容检测的具体过程,但随着频率的增加,功耗急剧增大,测量频率仅10kHz时,工作电流便达到36mA[1];利用施密特反相器构成的振荡电路是使用元器件最少的振荡型电容测量电路,但该方法对时间要求严格,须采用CPLD设计,而CPLD不能进行A/D转换和数据存储,需专门选择AD以及存储器,这又极大增加了电路体积;采用差动式直流充电法测量壳体电容是目前最先进的测压器采样电路,但所需时序较为复杂,且时序之间对于时间的要求较为严格,这些都不利于实际的火炮膛压测试系统。为此设计了基于逻辑时序优化的电容测压器采样电路。
1 电容测压器
1.1 电容测压器壳体
利用壳体本身作为敏感元件,实现壳体与传感器的一体化设计。整个测试系统置于内筒中,以内外筒为两极,测量极间电容。火炮发射时膛压使外筒发生弹性变形,内筒不动,内外筒两极板间距改变,电容值变化,测量由于壳体电容变化导致的电容两端的电压变化值,通过AD采集存储转换为数字量,最终与外部计算机相连,保存测试数据,并且用VB显示最后的膛压曲线。整个测压器结构如图1所示。
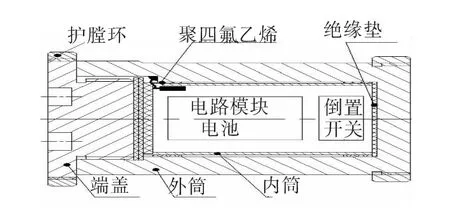
图1 电容测压器结构Fig.1 The structure of capacitance pressure device
1.2 当前最新的采样电路
目前最新的采样电路如图2所示。
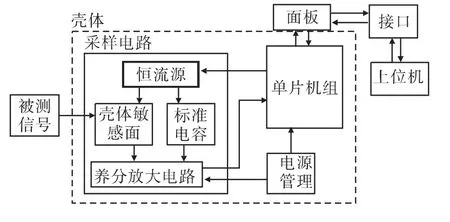
图2 最新的采样电路框图Fig.2 The latest sampling circuit block diagram
目前国内最先进的电容测量电路采用差动式直流充电法测量壳体电容,设计一个与壳体电容大小相匹配的标准电容,通过两个完全相同的恒流源分别给壳体电容和标准电容进行充电。由于壳体电容的变化使得测试过程中两电容两端充电电压不同,两电容两端电压经过电路的差分放大后,输入至单片机进行模数转换并存储。但该电路的不足之处在于逻辑时序相对复杂,且对各时序之间在时间上的匹配要求严格,由于各种因素造成的时间上的延迟易使时序间无法精确匹配,带来采样误差。
2 电容测压器采样电路
2.1 电容测压器采样电路
借鉴差动式直流充电法的电容测量电路,同样利用壳体电容作为测试敏感元件,设计了基于逻辑时序优化的电容测压器采样电路,使得电容检测从方法上得到进一步改进。
采样电路如图3所示,将壳体电容接入电路,并由后级的电压跟随器输出反馈至前级的电压比较器,使电路自身构成充放电振荡回路,通过单片机对采样电路经行控制,测试结束与上位机连接读数,通过测量壳体电容两端电压变化达到测试膛压的目的。
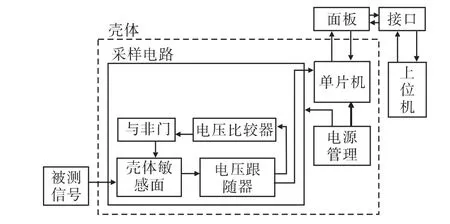
图3 采样原理框图Fig.3 Sampling theory block diagram
2.2 逻辑时序对比
从图4可以看出,原有的采样电路需要高低电平比例为9∶1的充放电信号CON、控制采数脉冲的事件标志信号ADT以及采数脉冲PWM波三个逻辑时序,且为了保证AD采样转换的准确性,不能在电容充放电的临界点进行采样转换,需要提前一定时间进行采样转换,这就对时间的精确性提出了很高的要求,且时钟之间的延迟也有可能导致采样的不准确。图5是改进后电路的逻辑时序,只需要一个采数脉冲PWM波即可,并且在采数脉冲的下降沿进行采样,对采集到的是电容变化的哪个阶段并没有特殊要求。
原有的采样电路由于受到采样频率的限制需要两片单片机同时采样以提高采样频率,而改进的电路只需要一片单片机进行采样即可,这不但减小了系统体积,使结构变得简单,同时使功耗相应的降低。相比以往电路具有一定的优越性。
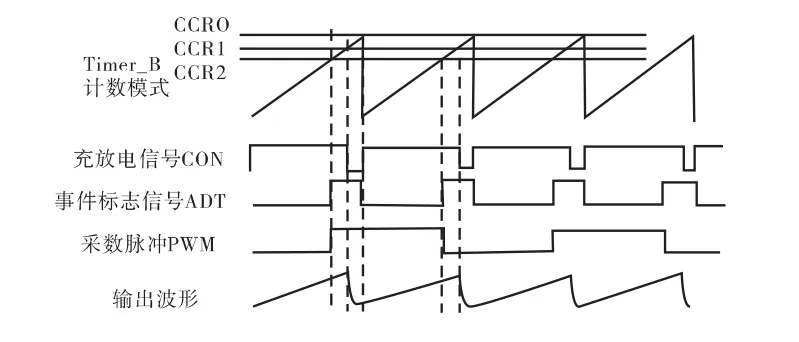
图4 原有采样电路逻辑时序Fig.4 The logic sequential of original sampling circuit
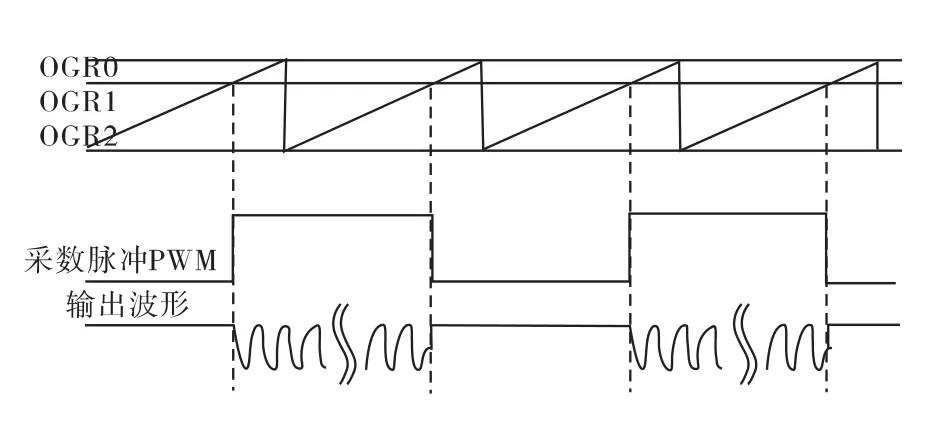
图5 改进采样电路逻辑时序Fig.5 The logic sequence of improving sampling circuit
3 误差分析
3.1 同轴电容值估测
本设计所采用的同轴圆柱型电容传感器如图6所示,内外筒相互覆盖的长度L为24mm,壳体外筒内径b为8.35mm,内筒外径a为8mm,两极板间距为d0=b-a,此时传感器的初始电容即为同轴圆柱电容测压器的电容值,计算如式(1)所示[2]。
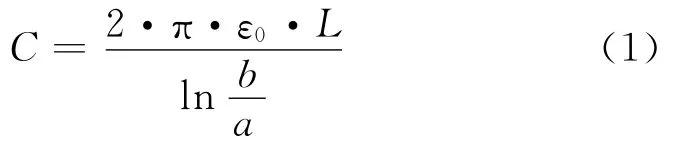
由式(1)可知,该电容传感器的理论初值为31.17pF。
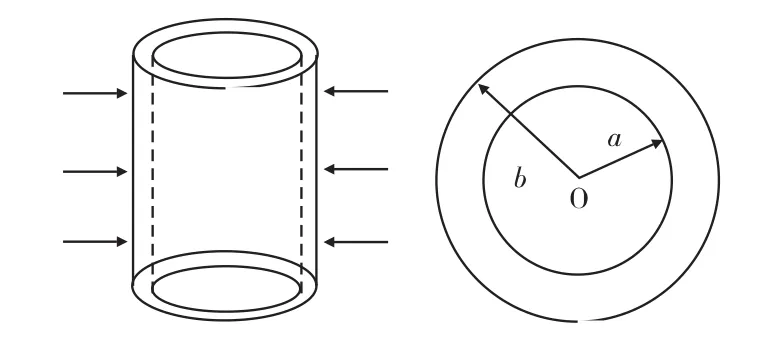
图6 同轴圆柱型电容测压器的示意图Fig.6The sketch map of coaxial cylindrical capacitance pressure device
3.2 平行轴电容值估测
同轴电容器内部电场具有对称性,可用高斯定理进行求解。当圆柱型电容器内外筒两轴不重合且为平行轴时,内部电场便不具有对称性,此时可以利用保角变换求解。
若平行轴圆柱型电容器轴间距为d,即0<d<b-a,电容器横截面如图7所示。
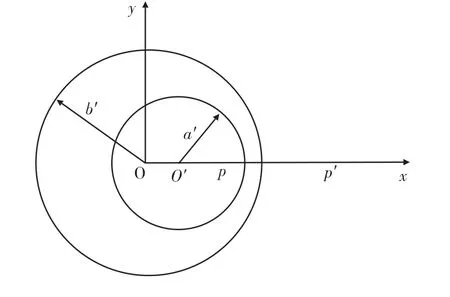
图7 平行轴圆柱形测压器截面Fig.7 The section of cylindrical pressure device of parallel axis
作分式线性变换,可将同一平面的两个圆变换为平面上的同心圆,如图8所示。
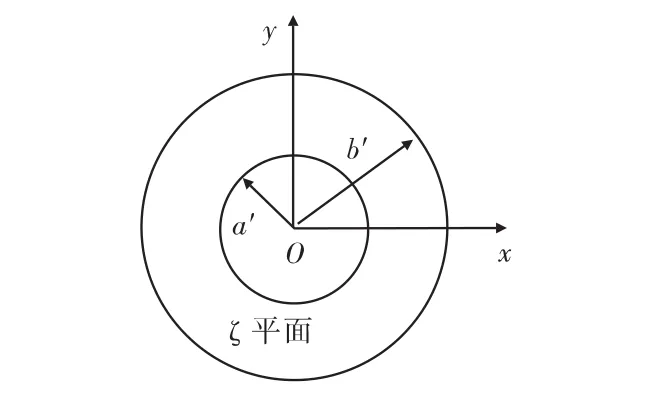
图8 分式线性变换Fig.8 inear transformation of fractional
利用同轴圆柱形电容器的结论,单位长电容[3]
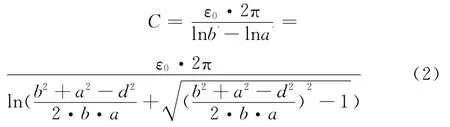
即平行轴圆柱型电容器电容为:
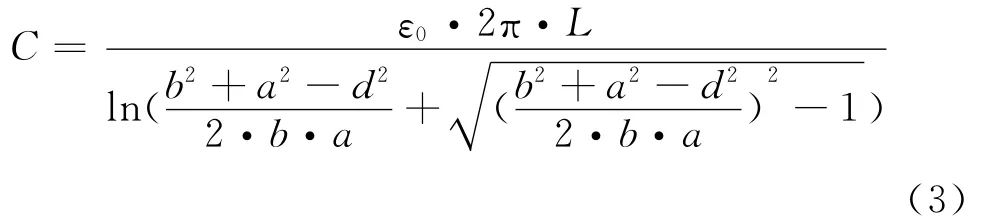
本设计中,固定内筒的聚四氟乙烯胶带单层厚度为0.1mm,内筒外筒半径差为0.35mm。假设聚四氟乙烯胶带缠绕内筒外壁3周,即内筒最大偏轴0.05mm,根据公式,平行轴电容值为31.49pF,同轴电容值为31.17pF,电容变化量为0.32pF,这对于31.17pF的基础电容来讲,可以忽略不计[4]。
3.3 偏轴电容值估测
将内筒放入壳体时,可能会出现内筒与外筒偏轴的状况。如图9所示,内筒半径为a,长度为L,外筒半径为b,内筒和外筒中心轴夹角为θ。
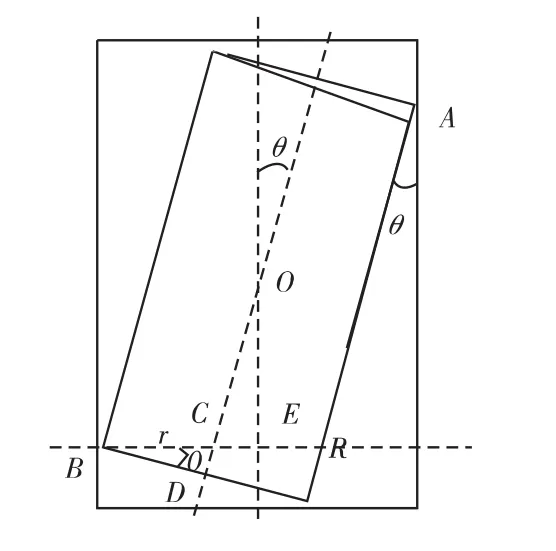
图9 内外筒偏轴示意图Fig.9 Schematic diagram of the inner and outer cylinder axis
可以得到如下关系[5]:
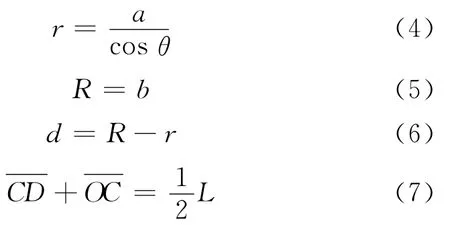
由上式可以得到θ的最大值为4.17°×10-3,即内外筒圆心偏移最大值为d=4.993×10-5mm,该倾斜轴状态的电容为C2。假设有一个平行轴圆柱形电容器,其轴间距d=4.993×10-5mm,电容为C1,则C2<C1。由公式可得C1=31.43pF,则倾斜轴状态的电容为C2对本系统电容传感器初值的影响完全可以忽略不计,也就是说偏轴对于本壳体的影响可以不予考虑。
综上所述,在本系统中,内筒在包裹聚四氟乙烯胶带后,即使出现偏轴和倾斜轴的两种状况,它们对传感器初值的影响可以忽略不计。
4 结论
根据电容测压器的特点,设计了基于逻辑时序优化的电容测压器采样电路。该电路由电压比较器、与非门以及电压跟随器代替了恒流源、标准电容和差分放大器,电路本身只需一个100kHz的逻辑方波信号,电路逻辑时序得到极大简化。试验表明,该电容测压器有较好的线性,测量范围0~600 MPa,灵敏度达到0.096pF/MPa,壳体安装等误差因素给测试带来的影响有限,验证了采样电路的可行有效。不足之处在于微小电容的测量易受到寄生电容等因素影响,给测试带来误差,如何进一步减小外部因素对电容测量的影响是下一步工作的重点。
[1]邱桂苹,于晓洋,陈德运.微小电容测量电路[J].黑龙江电力,2006,28(5):362.QIU Guiping,YU Xiaoyang,CHEN Deiyun.Tinycapacitance measurement circuit[J].Heilongjiang Electric Power,2006,28(5):362-366.
[2]舒乃秋.检测技术[M].北京:中国电力出版社,2006.
[3]孟立凡,蓝金辉.传感器原理与应用[M].北京:电子工业出版社,2007.
[4]金正国.复变函数与积分变换[M].大连:大连理工大学出版社,2009.
[5]王海明,裴东兴,张瑜,等.微小型放入式电子测压器的研究[J].电子设计工程,2009,17(12):28-31.WANGHaiming,PEI Dongxing,ZHANG Yu,et al.Research of micro drop-in electronic pressure device[J].E-lectronic Design Engineering,2009,17(12):28-31.
