基于改进梯度向量流动态轮廓模型的图像检测
2013-12-01胡鹏博刘晓利白宏阳
胡鹏博,刘晓利,白宏阳
(1.南京理工大学瞬态物理国家重点实验室,江苏 南京 210094;2.南京理工大学能源与动力工程学院,江苏 南京 210094)
0 引言
对自然背景中人造目标的分割,阈值分割方法很难取得良好的效果。阈值法的缺陷在于它仅仅考虑了图像的灰度信息,忽略了图像中的空间信息。在自然背景中,人造目标会出现光照不均,或者由于自身遮挡造成明显的亮面和暗面;当背景灰度位于目标亮面、暗面灰度之间时,阈值法几乎不能分割出完整目标。
Mandelbrot[1]提出的分形理论突破了传统几何整数维的限制,可以从不同尺度来刻画集合的几何特性,因此分形模型适合描述具有复杂和不规则形状的研究对象。目前,国内对这一问题已开展了较多的研究[2-4],提取图像分形维来区分自然背景和人造目标,主要方法有:1)基于分数布朗运动模型的分形维提取方法[5],该方法具有较好的检测效果,但计算时间太长;2)基于毯子法的分形维提取方法[6],该方法要求逐级计算不同尺度下的上下毯子,才能求出该尺度下的分形维,因此也需要较长的计算时间;3)微分计盒算法[7](DBC),计算速度快,但分形结果不精确。
为克服上述方法在逐点扫描、计算分形维效率低的缺点,本文提出基于分形理论和改进梯度向量流(GVF)动态轮廓(Snake)模型的人造目标检测算法。
1 分形基础与GVF Snake模型
1.1 分形维
分形可用于刻画对象的不规则性和自相似性。它突破了传统拓扑整数维的限制,从测量的角度重新定义了对象的维数,即分形维。这种维数可以是非整数,在效果上弥补了待观测对象中小于观测尺度的细节的损失。计算图像分形维的方法中微分计盒维数是广泛应用的一种。
微分计盒维数的思想是:设一幅灰度图像为f,取图像f中大小为M×M的图像区域,将其分割成e×e的子块(M/2≥e,e为整数),令r=M/e,表示分形的尺度。将图像想像成三维空间{x,y,z}中的曲面,x,y表示平面的坐标,z表示(x,y)处图像的灰度f(x,y)。在空间中,曲面向xy平面投影出许多e×e的网格,在每一个网格上,假想相应的曲面处于e×e×m的盒子中,其中m=256/r。
不断改变网格e的大小,可以得到一系列相应的盒子数 N(e),利用最小二乘法对log[N(e)]-log(e)进行拟合,所得直线的斜率即为该图像M×M区域的分形维。
分形维表达了一种特征,即具有以下性质[8]:1)具有精细的结构;2)不规则纹理,无论它的局部或整体都不能用传统几何语言描述;3)具有某种自相似或统计特性。因此,自然背景如天空白云、草地、树木、河流、沙漠等满足分形维的性质,而人造目标则不具备上述性质。
1.2 Snake模型
Snake模型是定义在图像域内的参数化曲线,以及能量函数,以最小化能量函数为目标,控制参数曲线变形,具有最小能量的闭合曲线就是目标轮廓。定义曲线为V(s)= [x(s),y(s)],其中:s是曲线的弧长,在长度归一化条件下s∈[0,1],构造以目标轮廓线V(s)为变量的能量函数:
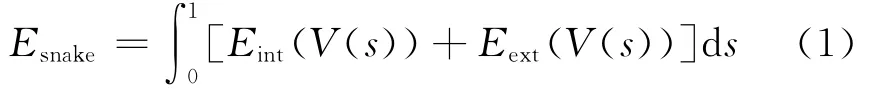
式中:Eint(V(s))为曲线的内部能量,定义如下:
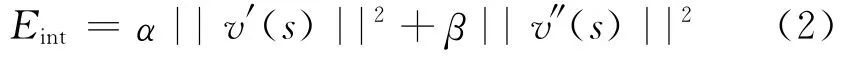
式(2)用来表征轮廓的固有特性。其中轮廓对弧长的一阶和二阶导数项表示其弹性势能和弯曲势能。Eext(V(s))为外部能量,一般定义为图像f的灰度梯度函数,目的是引导曲线演化到梯度较大的目标边缘处。
上述Snake模型有两个主要的问题[9]:轮廓的初始位置必须在目标轮廓线附近;难以逼近凹陷的边界。
1.3 GVF Snake模型
GVF Snake模型是一种改进的Snake模型[10],有效弥补了传统Snake的不足,该方法引入了一个新的静态外力场:
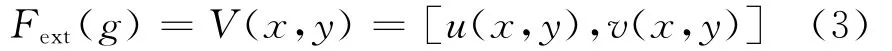
称为梯度向量流(GVF),替代传统Snake的外力场。u,v表示图像灰度在x,y两个方向上的变化,V(x,y)是在满足如下最小化条件下获得的,即
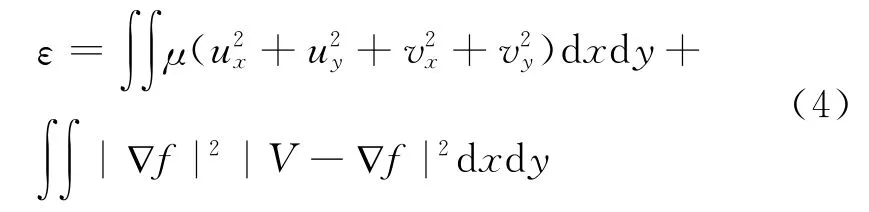
初始轮廓在V(x,y)作用下,向真实边缘逼近,当轮廓的总能量达到最小值时停止逼近,得到的轮廓即为真实轮廓。
2 基于分形和GVF Snake模型的目标检测快速算法
2.1 基于分形算法求目标初始轮廓
如图1所示,图1(a)为自然背景下轮船目标原始图像;图1(b)为其Canny算子检测结果,显然大量背景被检测出来;图1(c)为Ostu阈值分割结果,由于背景灰度处于轮船灰度亮暗之间,因此靠阈值分割无法将目标分割出来;图1(d)为据上述1.1节对原图分块运用微分计盒算法后得到的分形维图。可见,人造目标与背景有明显的灰度差别。
对分形后的图像采用Ostu大津分割法,分割出粗略目标,如图2(a)所示,图像中除了目标区域外,还有部分噪声块;运用形态学方法开运算、闭运算去除噪声,连接目标区域,结果如图2(b)所示。
提取轮船目标外轮廓,如图2(c)所示,作为Snake算法的初始轮廓。

图1 自然背景下轮船目标分形结果Fig.1 The fractal results of ship target under the background of nature

图2 轮廓提取过程Fig.2 The process of contour extraction
2.2 改进的GVF Snake模型
由于处理图像中部分目标内部结构复杂,很可能会导致目标外轮廓处梯度向量流受到干扰,进而使外轮廓收敛到目标区域内部,偏离了真实轮廓[11]。同理,背景中剧烈的灰度梯度变化同样会干扰轮廓的正确收敛。因此,对原图像梯度向量流进行改进,改进方法如下:
1)对原始图像f求初始轮廓各点位置p(x,y);
2)对每一点p(x,y),确定其邻域为目标真实轮廓潜在区域,邻域大小为36×36,处理后为图像g,如图3(a);
3)只对图像g求梯度向量流,替代原图GVF。
经过改进后,GVF由图3(b)变为图3(c)。可见,目标外大部分区域(图3(a)中黑色部分)的GVF为0,且目标轮廓边界区域的梯度变化剧烈,从而保证初始轮廓不会无限向外收敛到背景中;目标内部的部分区域(黑色部分)GVF为0,避免由于目标内部梯度变化剧烈程度强于目标轮廓区域,而导致初始轮廓收敛到目标内部。
GVF Snake模型算法流程图如图4所示,每循环一次,轮廓线进行一次迭代形变,进而逼近梯度变化最大的边界。循环次数N的确定与初始轮廓位置密切相关。

图3 GVF场示意图Fig.3 GVF schematic diagram
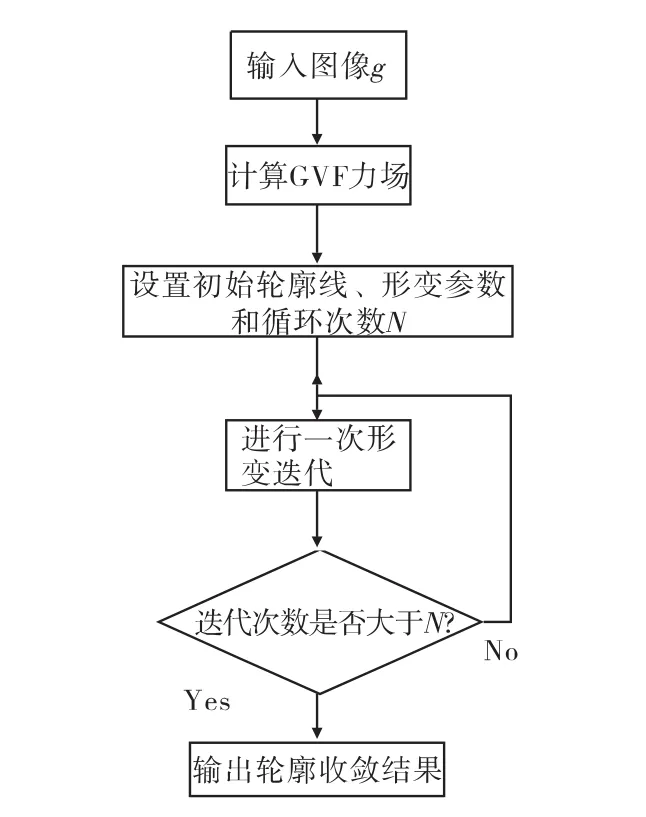
图4 GVF Snake模型算法流程图Fig.4 The flow chart of GVF Snake model algorithm
3 实验结果与分析
3.1 实验结果
将上述算法对270幅具有复杂自然背景和人造目标的图像进行检测,原图像素大小为512×512,示例图像见图5(a)。选取图像的背景均比较复杂,具有丰富的的灰度梯度信息;目标大小各异,灰度信息复杂,与背景灰度交错。经验证,普通阈值分割均无法分割出目标区域。实验程序在MATLAB 2009a环境下编写,在一台 Pentium(R)Dual-Core CPU,2.60 Hz,1.96GB RAM 的PC机上进行测试。
实际应用主要针对中、远距离(5~20km)自然背景中的人造目标进行检测。成像设备采用可见光CCD摄像头,视场大小为4°~5°,采集图像为8位灰度图像,帧频为PAL制式(25Hz)。目标可识别像素大小一般为16×16至256×256之间。
微分计盒算法中,将原始图像分割成多个16×16小区域(即M=16),对每个上述区域运用微分计盒法,依次设网格数e=2,4,8,16,求出相应盒子数,据最小二乘法求出此区域分形维。分形后的图像采用Ostu大津法分割出粗略目标区域,因为人造目标与自然背景的分形维存在显著性差异,经大量实验验证,分割阈值比较均固定,归一化后变化范围为0.4~0.45(8位灰度级范围约102~114)。Ostu大津法分割准则是使目标与背景类间方差最大化的过程,而本文需要尽可能多分割出目标区域,允许部分背景的存在,以方便Snake轮廓的收敛。因此,分割阈值可以有一定的变化范围(0~15)。
初始轮廓提取结果见图5(c),按照上一节2.3中的步骤对GVF进行调整,得到最终梯度向量流,用来指导初始轮廓收敛到目标轮廓,轮廓收敛第5次、第10次结果分别见图5(d)、图5(e)。可见,由于采用本文方法提取到的初始轮廓线已很接近真实目标轮廓,基本上迭代循环次数N取10次就能满足提取要求。
3.2 效率分析
下面分别从检测率和虚警率两方面介绍本方法在已建立图库中的表现。
表1中的分形算法检测率指分形算法正确检测到人造目标的概率。从表中可看出,本方法分形检测率很高,可以有效检测出自然背景中的人造目标,但若背景为城市或含公路,则会影响目标检测。
表1中的分形算法虚警率指分形算法在非目标区域中检测出目标的概率。虚警率与图像拍摄角度有关。如图6所示,左图中目标、背景均与CCD摄像头具有等效间距,右图中目标类似于左图目标,而背景(大地)相对于摄像头由近及远,具有不同的分形特征,靠近摄像头的大地纹理清楚细腻,分形维高,易干扰目标,增加虚警率;远处的大地纹理模糊,分形维低,不会干扰目标。
表1中的Snake轮廓提取率指在分形算法正确提取初始轮廓的目标中,正确提取出目标真实轮廓的比率。从中可以看出,对于大部分测试图像,初始轮廓可以有效收敛到目标真实轮廓,部分失败原因在于目标轮廓区域梯度变化弱于周围背景梯度变化,从而导致部分初始轮廓向背景收敛,影响目标轮廓结果。

表1 算法效率统计Table.1 The Statistics of Algorithm Efficiency

图6 不同角度的目标图像Fig.6 The object image with different angles
3.3 时间复杂度分析
将本文采用的微分计盒算法与经典分形算法中的毯子法[6]求分形维进行比较,通过Matlab仿真所需时间来比较结果,即调用Matlab函数cputime来求程序运行时间差。从结果可以看出本文提出的算法模型极大地缩短了运算时间,见表2(单位:s),其中列出了图5中前三幅图像的运行时间和图库的运行时间效率。
微分计盒算法对每一小块图像区域独立求分形维,而毯子算法需计算每一尺度对应的图像上下毯子,计算量大且内存开辟较多;同时,微分计盒算法采用分块扫描,避开了逐点计算分形维的运算,因而大大缩短了计算时间,使算法的实时性成为可能。
在XU ChenYang[10]的 GVF模型中,初始轮廓迭代次数一般为40次到上百次,才能逼近真实轮廓线,一般需要15~200s。在本文的GVF Snake算法中,由于初始轮廓已很接近目标轮廓,大大缩小了GVF Snake轮廓收敛次数,一般轮廓迭代次数控制在15次之内,所耗时间为3~7s,效率大大提高。
4 结论
本文提出基于分形理论和改进梯度向量流(GVF)动态轮廓(Snake)模型的人造目标检测算法。首先利用微分计盒算法计算图像各分块区域的分形维,粗略分割目标与背景;然后将分割边界作为Snake模型的初始轮廓,并依据分形结果修正和整体调整GVF场强分布;最后运用GVF Snake算法使初始轮廓准确收敛到目标真实边界。试验表明,该算法可以把目标从自然背景中准确快速提取出来,具有很好的鲁棒性,同时具有通用性,适于不同人造目标的检测。该算法可以用于复杂背景中人造目标的轮廓检测,为图像的进一步分析处理打下良好基础。
[1]mandelbrot B B.The fractal geometry of nature[M].San Francisco,CA:Freeman,1982.
[2]宿丁,张启衡.地空背景下目标分形拟合检测算法[J].仪器仪表学报,2006,29(4):581-589.SU Ding,ZHANG Qiheng.An edge detection algorithm based on fitting fractal model[J].Chinese Journal of Scientific Instrument,2006,26(8):640-641.
[3]朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011.
[4]LIU Wenping,HE Yingde.Fractal features and fuzzy clustering based tree leaf segmentation from images with the complex background[C]//International Conference on Computer,Mechatronics,Control and Electronic Engineering.US:IEEE,2010:317-321.
[5]刘宁波,黄勇,关键,等,实测海杂波频域分形有特性分析[J].电子与信息学报,2012,34(4):929-935.LIU Ningbo,HUANG Yong,GUAN Jian,et al.Fractal analysis of real sea clutter in frequency domain[J].Journal of Electronic & Information Technology.2012,34(4):929-935.
[6]Shmuel Peleg,Joseph Naor.Multipleresolution texture analysis and classification[J].IEEE Trans.Pattern A-nal.Machine Intell,1984,6(4):518-519.
[7]杨绍清,赵晓哲,林洪文.基于相对微分计盒法的人造目标分形检测[J].光学技术,2006,32(8):58-60.YANG Shaoqing,ZHAO Xiaozhe,LIN Hongwen.Fractal artificial detection based on relative differential boxcounting method[J].Optiacl Technique.2006,32(8):58-60.
[8]陈永强,陆安生,胡汉平.基于分形的图像分析方法综述[J].计算机工程与设计,2005,26(7):1781-1783.CHEN Yongqiang,LU Ansheng,HU Hanping.Summary of image analysis method based on fractal[J].Computer Engineering and Design,2005,26(7):1781-1783.
[9]范延滨,刘彩霞,贾世宇,等.GVF Snake模型中初始轮廓线设置算法的研究[J].中国图象图形学报,2008,13(1):58-63.FAN Yanbin,LIU Caixia,JIA Shiyu,et al.The research of contour initialization algorithm in GVF snake model[J].Journal of Image and Graphics,2008,13(1):58-63.
[10]XU Chenyang,Prince Jerry L.Snakes,shapes,and gradient vector flow[J].IEEE Transactions on image processing,1998,7(3):359-369.
[11]齐华,张健,刘军,等.基于梯度向量流模型的图像分割方法[J].探测与控制学报,2009,31(6):16-20.QI Hua,ZHANG Jian,LIU Jun,et al.Image segmentation method on GVF snake model[J].Journal of Detection and Control,2009,31(6):16-20.
