引信滚转角双闭环控制算法
2013-12-01高铭泽施坤林霍鹏飞祁克玉李红英
高铭泽,施坤林,霍鹏飞 祁克玉,李红英
(机电动态控制重点实验室,陕西 西安 710065)
0 引言
二维弹道修正引信是一种在引信原有功能基础上增加了二维弹道修正功能的新型引信,利用它可以使常规弹药获得精确打击能力,从而提高毁伤效率、减少附带毁伤并且大大降低作战成本。美国“精确制导组件”(Precision Guided Kit,PGK)方案[1]是目前国际上较为先进的二维弹道修正引信方案。PGK方案中,引信部分与弹体之间可以相对转动,引信部分安装有两对固定的翼面,其中一对为导转翼面,另外一对为修正翼面。弹丸出炮口后引信部分在翼面导转力矩和极阻尼力矩的作用下迅速减旋,并形成向左的平衡转速。引信部分以一定的转速转动时,升力翼面产生的升力沿弹径方向旋转,因此对弹道无显著影响。当需要进行弹道修正时,通过调整电磁力矩控制引信滚转姿态,使之相对大地坐标系固定在确定的滚转角度,这样升力翼面产生的升力将持续作用在这个方向,从而改变弹丸飞行轨迹最终达到弹道修正的目的。可见引信滚转角控制是实现弹道修正的关键,而在PGK控制方案的专利[1]中并未提到有关控制算法的技术细节。因此本文针对二维弹道修正引信滚转角控制问题,研究了一种基于滚转角位置和速度反馈的滚转角双闭环控制算法。
1 引信滚转运动及受力情况分析
引信减旋完成达到平衡转速后,主要受到翼面导转力矩Mx、轴承摩擦力矩Mg、极阻尼力矩Mxz以及电磁控制力矩Me等的作用。其中导转力矩Mx方向由固定翼的安装方向决定,为逆时针方向,大小由翼面偏置角和弹道环境决定;由于引信与弹丸相对转动,引信将受到阻碍引信与弹体的相对转动的轴承摩擦力矩,且由于弹丸始终高速右旋,则引信受到的轴承摩擦力矩Mg方向始终为顺时针方向,其大小与相对转速及摩擦系数等参数有关[3];由于引信存在滚转速度,故将受到极阻尼力矩的作用,其方向与引信转速相反,大小与转速成正比,考虑到引信平衡转速很低,此时引信所受的极阻尼力矩也很小,此处可忽略其影响。在系统需要进行弹道修正的时候,可以通过施加电磁力矩Me以调整引信滚转姿态,电磁力矩Me总是阻碍引信与弹体相对转动,即其方向为顺时针方向,大小可以控制;引信受力情况如图1所示,所有力矩方向均是由弹尾观察所得。
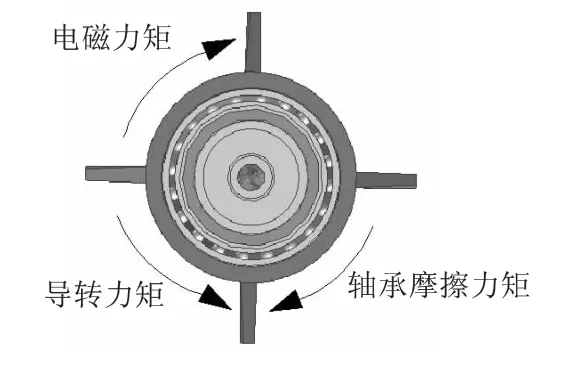
图1 引信受力情况简图Fig.1 Force diagram of the fuze
2 滚转角双闭环控制算法
2.1 滚转角控制模型
滚转角控制模型以引信需要悬停的目标滚转姿态、引信实际的滚转姿态以及滚转速度为系统输入,计算需要施加的电磁力矩,在此力矩作用下引信滚转姿态和滚转速度将发生相应的变化,通过测量装置测量出更新后的引信滚转姿态和滚转速度,反馈到系统输入中,形成双闭环控制回路,使得系统总是输出合适的电磁力矩,最终达到引信滚转姿态控制的目的。滚转角控制模型如图2所示。
控制力矩计算过程如下:首先由二维弹道修正系统中的导航与制导模块计算引信需要悬停的目标滚转姿态,并利用滚转姿态测量模块解算引信实际滚转姿态,两者比较后得到引信需要转过的角度,再结合引信的实际转速通过两次微分的方式计算出完成控制所需的合力矩,最后从合力矩中去掉导转力矩以及轴承摩擦力矩,即可得到需要的电磁力矩输出。引信在此电磁力矩的牵引下,旋转至新的位置,并将此位置通过引信滚转角测量模块测量其姿态和转速信息后,分别传至系统输入端,进行下一次的滚转角控制计算,如此循环往复可以将引信的滚转角控制在需要的位置。其中导转力矩与弹丸飞行马赫数有关,故该模型中还需输入弹丸飞行速度、高度、实测气象条件及导转力矩系数表等信息。
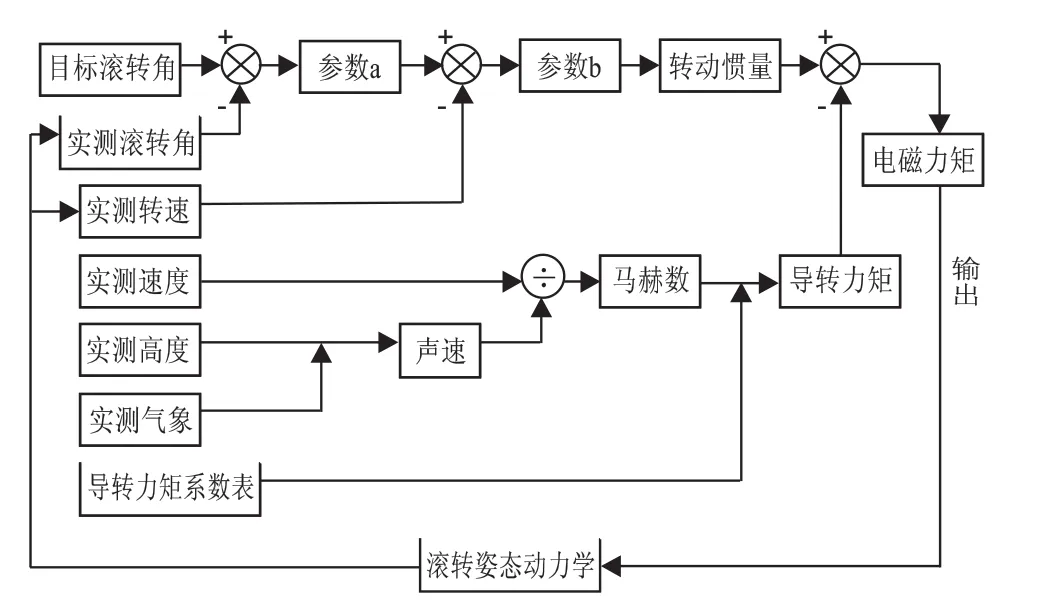
图2 滚转角控制模型Fig.2 Control model of the roll angle
2.2 导转力矩Mx的计算
由图2可知要计算电磁力矩Me必须先计算导转力矩Mx,故首先讨论有关导转力矩Mx的计算。Mx与弹丸空速v、马赫数Ma及导转力矩系数mx等有关,故首先根据弹道测量和实测气象等信息计算v、Ma和mx。利用弹丸高度h插值实测气象数据,得到当地气压P,虚温τ,风速vw,风向φw,由实测气象信息及弹丸飞行高度可以得到当地声速C,进而计算出弹丸飞行马赫数Ma,如式(1)所示:

其中v为弹丸空速且v=vgps-vw,vgps是GPS测量得到的弹丸速度信息。通过上式计算的马赫数可以插值得到导转力矩系数mx,进而由式(2)计算得到导转力矩Mx。其中导转力矩系数mx以表格形式提供,由工程算法或流体动力学仿真计算得到。
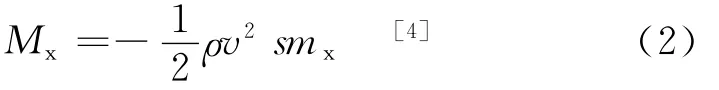
其中ρ为空气密度,s为弹丸最大横截面积。空气密度ρ可由实测气象信息中的当地气压P,虚温τ计算得到。
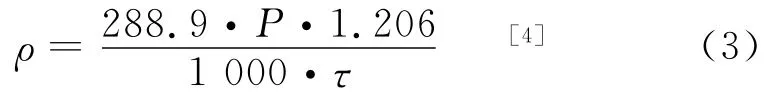
2.3 合力矩M的计算
由引信的受力情况可知,以右旋为正方向,Mx和Mg的大小和方向无法人为控制,Mx的方向始终为负,Mg的方向始终为正。电磁力矩Me的方向只能为正,且其大小可以人为控制,通过调整Me的大小可以控制引信滚转运动,滚转角双闭环控制算法就是根据弹道测量和辨识信息、制导信息来计算合适的电磁力矩Me,以完成引信滚转姿态控制。
根据制导算法计算的引信滚转姿态的目标值γxz,对比实测引信滚转角γx,得到引信需要旋转的角度Δγ,同时考虑实测引信转速ω,根据式(4)计算完成滚转控制所需的合力矩M。
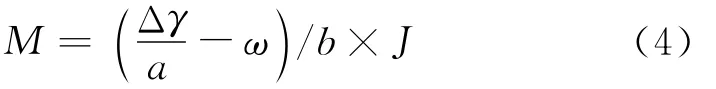
式(4)的计算思路是对转角进行微分得到需要的角速度,将之与实际角速度比较后再次微分,再乘以转动惯量J就是控制所需合力矩M。由于系统属于离散控制系统,故微分的形式转化为式(4)中的差分形式,而符号a和b为可调参数,通过这两个参数可以调整转角控制系统的超调量、调节时间等特性。经过仿真验证,参数a主要影响系统的超调量,a越小超调越大,过大的超调量会导致调节时间变长;参数b主要影响系统的调节时间,b越小,调节时间越短;根据目前系统的配置,取a=0.2,b=0.01时控制结果较好。
2.4 电磁力矩Me的计算
根据引信的受力分析可知,引信所受的合力矩M是电磁力矩Me、轴承摩擦力矩Mg以及导转力矩Mx的和,因此电磁力矩Me可通过式(4)得到:
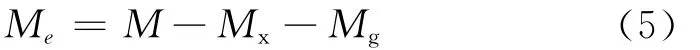
由式(5)可知,计算电磁力矩Me需要计算导转力矩Mx与轴承摩擦力矩Mg,其中导转力矩Mx可由式(2)计算得到;轴承摩擦力矩Mg与引信部分和弹丸之间的相对转速以及摩擦系数等有关,由于相对转速在转角控制过程中变化范围不大,故以一固定值代替。
得到式(5)右边各项后,即可计算转角控制所需的电磁力矩Me,最终将计算的Me作为算法输出,传递给磁电机控制电路。同时,由于电磁力矩Me的取值范围有限,必须保证最终得到的电磁控制力矩在其取值范围(0~Mmax)之内,因此当电磁力矩Me的计算结果为负值时,取Me=0;当电磁力矩Me的计算结果大于Mmax时,取Me=Mmax。
3 仿真验证
为了验证本文提出的滚转角控制算法的控制效果,以122mm底凹榴弹为平台建立6自由度弹道仿真模型,并利用上述滚转角控制算法进行引信部分转角控制仿真,仿真过程中假设分别需要向前、后、左、右四个方向进行修正,即所要求的目标滚转角分别为90°,180°,270°,360°四种情况[5]。同时假设弹丸飞行到24s时完成第一次落点预测,即第24s开始进行滚转角控制。仿真结果显示四种情况下,利用本文滚转角控制算法可将滚转角控制在所需要的位置,并且基本没有超调,到达目标位置后波动也较小,其中目标滚转角为270°的结果如图3所示。
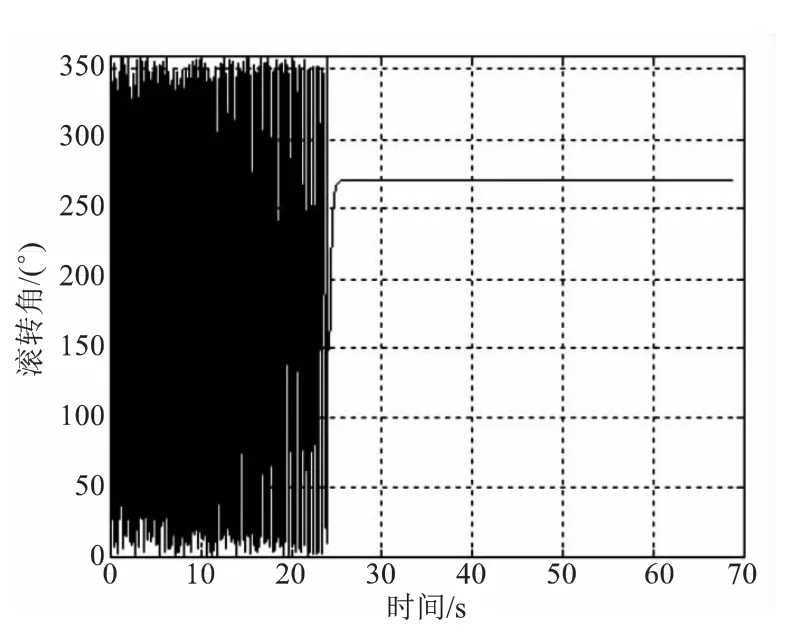
图3 滚转角控制仿真结果Fig.3 control simulation results of roll angle
由图3可知在27s之前滚转角控制已经达到稳定状态,故为了更清楚的表示控制结果,将图3中23~27s的一段单独取出观察,如图4所示。
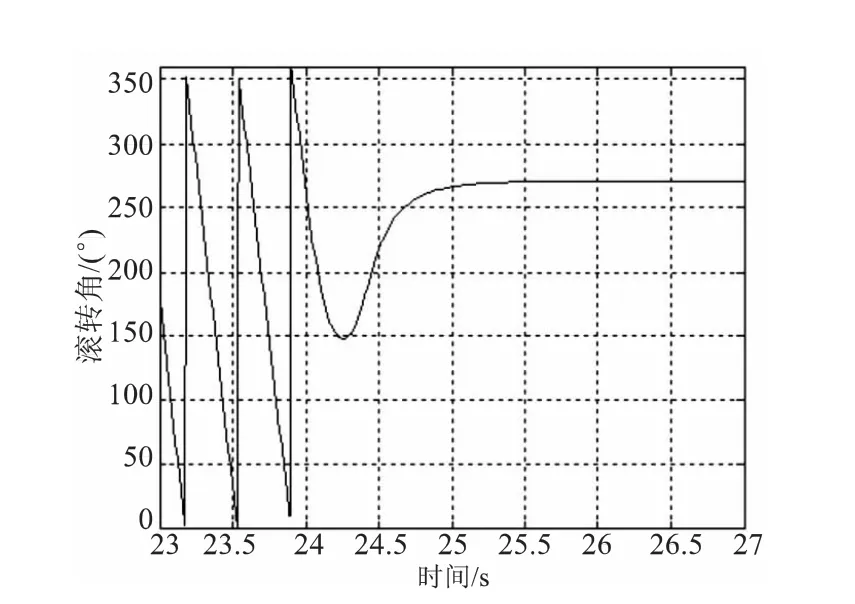
图4 滚转角控制结果局部放大Fig.4 Fractionated gain of control simulation results
图4清晰地显示出在第24s开始修正后,系统在1s内到达目标滚转角,稳态时的波动和误差都较小。通过对仿真结果中转速和电磁力矩的观测,发现转速在开始控制后一直保持在较小的状态,电磁力矩在取值范围之内,变化较平稳。仿真结果表明,算法在不引入误差的情况下,不存在超调量,调节时间较短,稳态误差较小,稳态波动接近于零,满足滚转角控制的系统要求。转速和电磁力矩的变化也保持在较小的范围内。
为了验证控制算法的实用性,分别对系统在导转力矩计算存在误差和滚转角测量存在误差的情况下进行了仿真。当导转力矩的计算误差为50%的情况下,仿真结果表明引信滚转角稳态时存在一个渐变的偏移,但偏移量相当小,仍然可以实现对滚转角的控制;滚转角测量引入均值为2°,均方差为5°的正态误差,仿真结果显示系统在稳态时存在一定的偏移,并且围绕着稳态滚转角度有3°上下的振动。同时引入导转力矩计算和滚转角测量两种误差时,滚转角控制仿真结果如图5所示,可见控制结果存在一定的偏移量和波动,对稳定状态的控制结果进行统计分析可知,引信滚转角控制存在均值为2.65°,均方差为2.43°的误差,该误差能够满足修正系统对引信滚转角控制的要求。
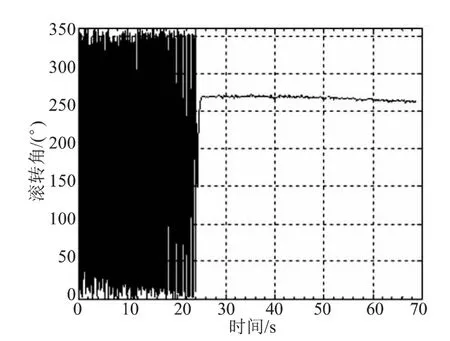
图5 两误差同时添加的仿真结果Fig.5 The simulation results also added two error
4 结论
本文提出了一种二维弹道修正引信滚转角双闭环控制算法。首先根据实测气象条件计算引信所受的导转力矩;然后以实测滚转角与目标滚转角的位置为依据,计算引信需要旋转的角度,结合引信实际滚转速度计算需要施加在引信上的合力矩,进而求出所需的电磁力矩;引信受到电磁力矩作用后实际滚转姿态与滚转速度可由姿态测量模块解算得到,并作为反馈信息代入下一时刻的实测滚转角和滚转速度,更新输出的电磁力矩,形成双闭环的控制回路,使得系统总是可以输出合适的电磁力矩,以达到控制引信滚转姿态的目的。仿真结果表明,文中滚转角控制算法可以满足二维弹道修正系统对滚转角控制的要求,达到相应的控制准确性,快速性和稳定性。但由于气象条件的变化和系统响应时间的影响均会引起一定的误差,故这些因素以及其他因素可能代入控制算法的误差,还需进一步研究。
[1]John A Clancy,Eden Prairic,Thomas D Bybee,et al.Fixed Canard 2-D Guidance of Artillery Projectiles:U.S.,US6,981,672B2[P].2006-01-03.
[2]Viljoen G T,R Ldu Plessis.Despin and roll attitude control of 2Dguided fuze kit[C]//26th International Symposium,Ballistics,2011.
[3]孙新.弹道修正弹鸭舵修正方法研究[D].南京:南京理工大学,2005.
[4]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.
[5]侯宏录,王赛,闫帅.弹道参数对弹丸落点的影响分析[J].西安工业大学学报,2009(3):5-8.HOU Honglu,WANG Sai,YAN Shuai.Effect of the ballistic parameters on bomb falling point[J].Journal of Xi'an Technological University,2009(3):5-8.
