基于扩展卡尔曼滤波的射程修正落点预测模型
2013-12-01陈维波纪永祥陈战旗
陈维波,纪永祥,陈战旗
(1.西北工业大学航天学院,陕西 西安 710072;2.中国华阴兵器试验中心,陕西 华阴 714200)
0 引言
为了满足现代战争的需求,精确打击,远程火力压制和远程火力支援弹药将得到大量的应用,而传统的常规炮射弹药不能达到对敌作战的预期效果,弹道修正弹就是在此背景下诞生的一种成本低、精度高、射程远、能批量生产并适合现代战争需要的强力打击弹药,弹道修正弹药在同样毁伤概率的条件下,可以减少大量的普通弹药消耗量。而目前将大量生产装备的无控弹药装备弹道修正引信,就可实现简单的弹道修正,大幅度提高命中精度或落点散布,其效费比之高是难以估算的,具有重要的军事和经济意义。
在评估一维弹道修正引信的修正效能时,以往采用单发交叉对比射击试验法,即利用非修正弹药和修正弹药在近似条件下独立射击,对比两种弹药的散布差别,得到修正弹药的修正效能试验结果。这种试验方法的缺点就是两组弹药、两次射击实施不可能达到试验条件(包括弹药条件)上的完全一致性[1],可比性较差,而且存在弹药消耗大、试验成本高的问题,因此提出基于扩展卡尔曼滤波的射程修正落点预测模型,以期解决上述问题。
1 新方法与扩展卡尔曼滤波介绍
1.1 新方法介绍
针对一维弹道修正引信修正效能评估采用传统试验方法存在试验条件一致性差、用弹量大的问题,通过利用对弹道动态过程深度测试,获得修正点前的弹道参数,在此基础上利用弹道仿真的方法,获取修正点后未修正虚拟弹道及落点预测数据,比较修正弹落点数据(阻尼机构工作)和预测落点数据(阻尼机构不工作),得到修正效能试验结果。修正效能方法示意图如图1所示。
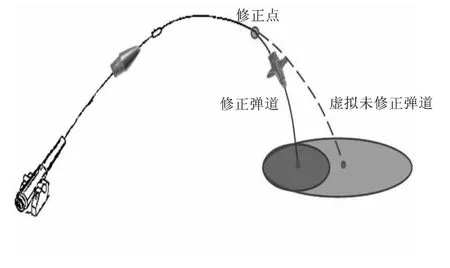
图1 修正效能方法示意图Fig.1 The method of range correction efficiency
上述试验方法实施的关键有以下两点:
1)修正点前弹道数据的测量精度。
后续未修正的虚拟弹道辨识所需的初始参数来自于修正点前的弹道测量数据,故测量获得的弹道参数的精确将直接影响弹道辨识的准确性。
2)弹道辨识算法的选择。
目前国内自主式弹道测量和辨识技术主要有3种:基于弹道最小速度点的速度值及其出现时间的辨识方法;基于速度-时间序列的弹道辨识方法;基于比较名义弹道与实际弹道在上升初始段的水平距离来实现对弹丸射程偏差的预测方法。这三种技术都是基于实时性需要而提出的。
在靶场修正效能试验中弹道辨识有其自身特点:一是未修正弹道进行辨识所需参数和实际射击的修正弹道参数在阻尼机构打开前是完全相同的,如图1所示;二是测量数据精度相对弹载设备较高,由此获得的弹道辨识所需影响弹道散布的参数其真实性和准确性也较高较多;三是阻尼机构打开时间点很难测到,由于遥测不易实现,黑匣子又难以回收,弹道测量不易捕获和确定,在阻尼机构工作段弹道没有明显的特征点时,很难判断出准确的阻尼机构打开时间点;四是弹道辨识实时性要求不高,靶场试验试后数据处理,不要求实时性。
1.2 扩展卡尔曼滤波原理介绍[2]
1960年,卡尔曼发表了用递归方法解决离散数据线性滤波问题的论文《线性滤波与预测问题的新方法》,在这篇文章里,一种克服了维纳滤波缺点的新方法被提出来,这就是我们今天称之为卡尔曼滤波的方法。卡尔曼滤波是一种最优化自回归数据处理算法,广泛应用于机器人导航、控制,传感器数据融合以及导弹追踪等方面。它可以估计信号的过去和当前状态,甚至能估计将来的状态[3]。
将卡尔曼滤波推广用于非线性系统称之为扩展卡尔曼滤波[4]。设其系统方程和量测方程如下:
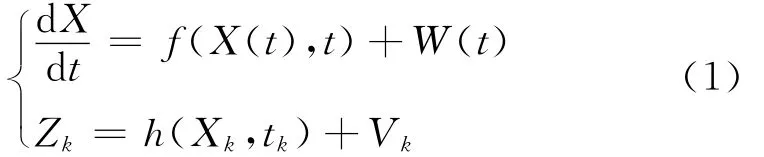
其中W(t)为过程噪声,Vk为量测噪声,假定均为高斯零均值白噪声,且彼此不相关。
首先采用Taylor展开线性化的方法将方程(1)线性化,然后对线性化的方程离散化,得到离散动力学方程(2)[5]。
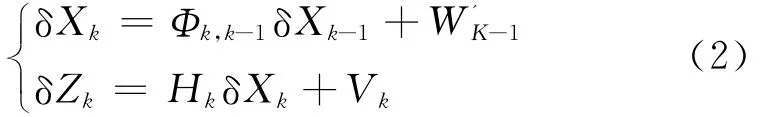
最后采用如下卡尔曼滤波预测的基本公式迭代计算获得预测结果。
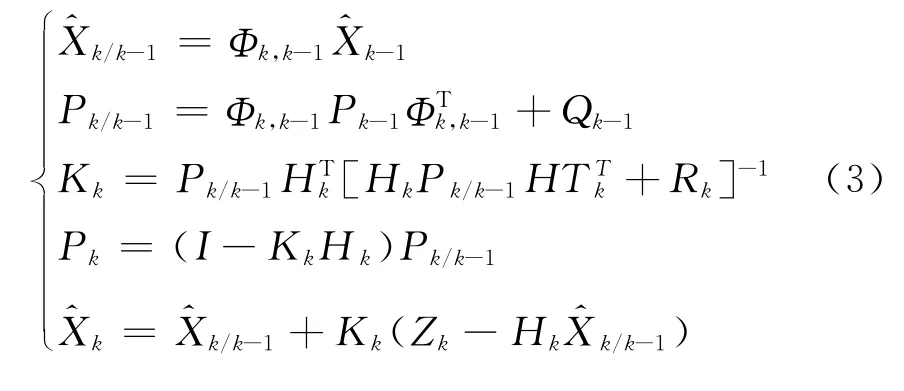
2 扩展卡尔曼滤波射程修正落点预测模型
在靶场的弹丸飞行辨识中,遇到的是非线性连续—离散系统,即状态方程是非线性连续型的,观测方程是离散型的,则根据上述分析,可建立扩展卡尔曼滤波方程对弹丸射程修正落点进行辨识和预测,其模型主要包括基于弹丸速度、弹道倾角、位置坐标、气象等状态变量的状态方程和基于测试雷达与飞行弹丸的斜距、方位角、高低角以及气象等观测变量的量测方程。
2.1 状态方程
考虑到测试雷达可提供的量测数据,本文以质点弹道模型[6]为基础,建立弹道滤波及落点预测的状态方程模型。
取状态变量 X(t)= [v,θ,x,y,z,p]T,则扩展卡尔曼滤波预测的系统状态方程为:
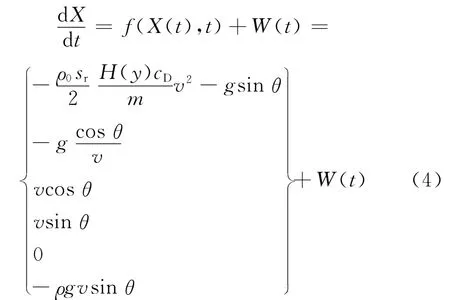
式中v为弹丸的速度,θ为弹道倾角,x、y、z为弹丸空间三维坐标,p为气象数据,ρ0为空气密度,sr为弹丸直径 ,m为弹丸质量,g为重力加速度,H(y)为空气密度函数,cD为阻力系数 。假定W(t)为零均值高斯白噪声,且服从方差为Q的正态分布,即W(t)~N(0,Q)。
2.2 量测方程
在靶场试验时,测试雷达的直接观量测数据有测试雷达与飞行弹丸的斜距r、方位角β、高低角φ以及气象数据p。则取观测变量Xk= [r,β,φ,p]T,则观测方程为:

假定Vk为零均值高斯白噪声,且服从方差为R的正态分布,即Vk~N(0,R)。
2.3 算法流程
1)利用测试雷达测量修正弹在修正点前的弹道数据,利用公式(4)和(5)对弹道数据进行滤波处理,得 到 高 精 度 的 修 正 点 的 弹 道 参 数 (v0,θ0,x0,y0,z0),即落点预测的初始值;
2)利用处理后的弹道参数和弹道模型进行弹道参数辨识,得到修正点后未修正弹道的弹道系数;
3)根据获取的高精度修正点弹道参数(v0,θ0,x0,y0,z0)及修正点后未修正弹道的弹道系数,利用弹道模型进行仿真计算,得到未修正弹道的预测落点数据。
在应用扩展卡尔曼状态参数估计方法辨识弹道时,关键是准确估计过程噪声和测量噪声特性,估计不准确,将可能导致系统不稳定,计算结果与实际弹道有较大出入,实际计算时是通过对修正点前的测量弹道过程噪声和测量噪声估计,将其应用于修正点后未修正弹道的预测。
3 试验验证
3.1 验证思路
对引信修正效能试验而言,不仅仅是要求弹道辨识结果误差较小,更重要的是辨识弹道落点散布与实际弹道落点散布相一致,否则就会失去了试验意义。故试验验证的思路是:将某型弹一组实际弹道通过设置某一典型时间点作为修正机构工作点,对该时间点后的弹道应用上述方法进行辨识预测,并与实际弹道落点相比较,获取其落点预测误差值;并对预测弹道与实际弹道应用弹道一致性方法进行检验,检查密集度试验结果是否存在显著性差异;最后判断预测弹道落点数据能否代替实际弹道落点数据。
3.2 验证试验
一维弹道修正引信7发,配某型火箭弹,装定为不修正状态,在常温条件下,以45°射角对地射击。测试弹丸全弹道速度、空中位置坐标等参数及落点数据。假定修正机构工作时间点为58s,根据建立的弹道滤波和预测模型及测试数据,得到修正机构不工作时的落点数据,如表1所示。比较预测落点数据与实测落点数据,计算得到落点预测误差不大于射程的0.6‰;预测落点与实测落点数据应用弹道一致性方法进行检验,密集度检验结果无显著性差异;故预测落点数据可以代替实际弹道落点数据,与修正后的落点数据进行比较,以考核和鉴定修正弹的修正效果。
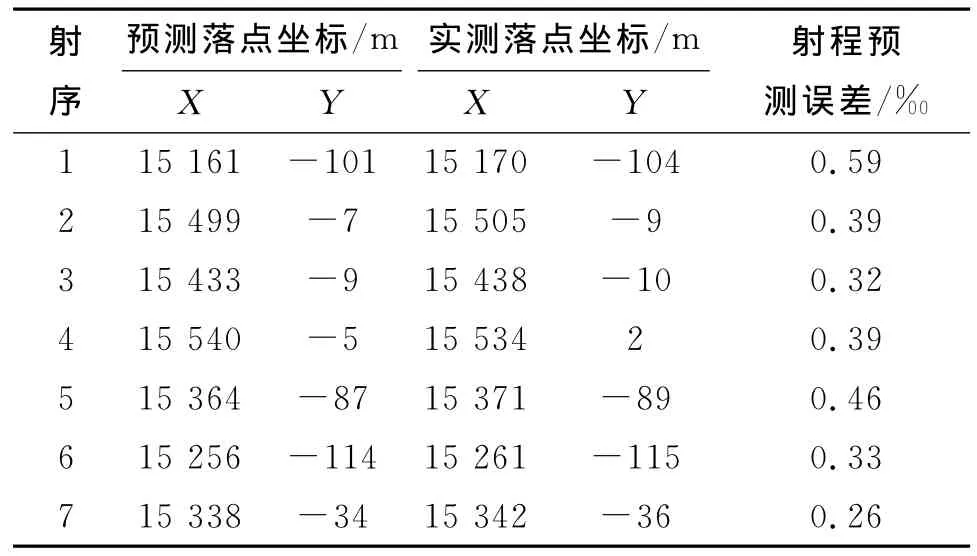
表1 预测落点坐标与实测落点坐标对比表Tab.1 Forecast and the measured coordinates contrast table
3.3 试验结果分析
上述分析及试验结果表明:应用扩展卡尔曼滤波和预测技术,一是可以适用于弹丸飞行这个连续的动态非线性过程;二是既可以对测量弹道进行滤波提高数据处理精度,又可以对后续弹道预测辨识;三是对阻尼机构打开时间点准确性要求不高,理论上在阻尼机构工作点前任何时间点都可以由弹道滤波转为弹道预测,当然由弹道滤波转为弹道预测的时间点距阻尼机构工作点越近,预测的弹道越准确,但是不要求严格准确的阻尼机构打开时间点;四是未修正测量弹道滤波和未修正虚拟弹道预测辨识所用状态方程相同,虚拟弹道预测所需参数来自滤波后的测量数据或由测量数据计算得到,与弹丸飞行中的实际参数基本相同,辨识出的弹道更准确,更接近实际弹道。
综上所述,用扩展卡尔曼滤波预测技术处理实际弹道测量参数并进行弹道辨识,结果更准确,精度更高,而且用弹量少。
4 结论
在评估一维弹道修正引信的修正效能时,以往采用修正弹与非修正弹各射击一组,对比落点的方法进行评估,存在试验条件一致性差、用弹量大的问题。本文建立了基于扩展卡尔曼滤波的射程修正落点预测模型,该方法考核修正效能时,只需要射击一组修正弹,依据修正点前的实测弹道参数预测非修正弹落点,然后以预测的非修正弹落点与修正弹落点对比,即可得到试验结果。最后通过射击试验对该模型进行了验证,结果表明预测得到的弹道精度较高,与实际弹道在射程和密集度上无显著性差异,该方法可用于评估一维弹道修正引信的修正效能。
[1]王兆胜,郭锡福.诸元精度与密集度对命中概率的影响[J].弹道学报,2003,15(1):64-67.WANG Zhaosheng,GUO Xifu.Influence on hitting probability by accuracy of firing data and dispersion[J].Journal of Ballistics,2003,15(1):64-67.
[2]王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社,2004.
[3]史金光,徐明友,王中原.卡尔曼滤波在弹道修正弹落点推算中的应用[J].弹道学报,2009,20(3):41-43.SHI Jinguang,XU Mingyou,WANG Zhongyuan.Application of kalman filtering in calculation of trajectory falling point of trajectory correction projectiles[J].Journal of Ballistics,2009,20(3):41-43.
[4]姚俊,张玉春,李娜.基于广义Kalman滤波算法的弹道参数辨识[J].沈阳理工大学学报,2008,27(3):1-4.YAO Jun,ZHANG Yuchun,LI Na.Identification of trajectory parameters based on generalized kalman filtering algorithm[J].Transactions of Shenyang Ligong University,2008,27(3):1-4.
[5]成光,刘卫东,魏尚俊.基于卡尔曼滤波的目标估计和预测方法研究[J].计算机仿真,2006,23(1):8-10.CHEN Guang,LIU Weidong,WEI Shangjun.Methods for estimation and prediction of maneuverable target based on kalman filtering[J].Computer Simulation,2006,23(1):8-10.
[6]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.
