基于查询和相对收益的物化视图选择算法

彭 成，佟秋利

（1.清华大学 计算机科学与技术系，北京100084；2.清华大学 计算机与信息管理中心，北京100084）

0 引 言

在多维联机分析系统中，将数据进行聚集生成物化视图预先存储起来，对一些查询可以直接给出结果，而不必进行聚集计算，提高了查询的效率。物化视图需要占用空间，对于高维度的数据集来说，可以生成的物化视图的总个数随着维度上升成指数级增长，需要进行物化视图的选择。

目前物化视图选择的策略较多，但是并没有得到普遍的最优算法，物化视图选择调整问题本身也被证明为NPHard问题［1］。在数据仓库系统运行过程中，对着用户查询的不断变化，已有的选择策略可能并不能满足当前的用户查询习惯，如何准确地把握用户查询类型的分布，并选择合适的时间段进行调整，是当前研究的重要问题。

Theodoratos D提出了对物化视图定期地进行动态调整的方法，通过判断用户一段时间内的查询情况变化，结合物化视图本身的查询代价综合考虑，选择合适的时间进行调整。除了这种阶段性调整的方式之外还有实时动态调整的方式，Cohen E提出了按照查询请求的变化来实时改变每个物化视图的优先级，进行实时调整。不过这种方式调整又过于频繁，对于查询请求比较多的情况下不适用，另外视图集经常变化，不够稳定，对于随机性强的查询并不是很实用。

本文提出了根据查询进行动态调整的选择算法，同时又考虑到视图的收益和占用空间，而且可以由用户自行设定维属性权重，不断调整出最适合的物化视图选择方案。

1 物化视图概念介绍

为了能够更快地得到查询结果，在多维联机分析系统中，也会采用类似于视图的策略，将数据进行聚集处理并预先存储起来作为中间结果，当查询访问需要利用到其结果时可以直接给出，而不必进行聚集计算，这个中间结果便是物化视图。对于传统的二维数据库，视图的存在方便了查询，但是视图本身是一个虚表，并不真实存在，只是方便用户浏览的一种形态，在实际查询时还是会调用原始数据库进行计算，在效率上并没有提高，查询时也需要重新进行计算。而物化视图则不同，它是真实存在的中间结果，可以提高查询的效率。在OLAP查询中，有时会遇到很复杂并且需要调用多个维度，涉及到多种数据的查询，这个时候需要对数据进行连接、投影等操作，其对时间的消耗是很大的，如果每次都需要进行重新计算，则满足不了联机分析系统对查询的快速响应要求。物化视图的出现解决了这一问题，它对可能需要调用到的结果事先进行投影、连接、选择等操作生成中间数据并存放起来，是真实地存放在数据仓库中的，每次查询时可以直接从物化视图返回结果，提高了查询的效率。

2 物化视图的选择及调整

物化视图的存在使得数据仓库获得了较快的查询速度，物化视图的选择策略对查询速度有着决定性的影响。目前物化视图选择的策略较多，但是并没有得到普遍的最优算法。完全物化的数据集的数据量随着维度数量而指数级增长，对于高维度的数据仓库，完全物化并存储是难以实现的。因此，就需要选择其中部分的物化视图来存放，即物化视图的选择策略问题，在特定的空间限制条件下，选择出合适的物化视图集，使得数据仓库对用户查询有着最快的响应。

物化视图的选择策略一般由3个方面因素决定：存储空间占用，维护代价以及生成物化视图带来的收益。

（1）存储空间占用：由于物化视图的大小各不相同，维度包含的越多，数据划分的越精细的物化视图一般占用的空间较多，即使它可以为用户节省很多的时间，但是有时将空间节省下来存放更多的占用空间较少的物化视图更为划算。从本质上来说，物化视图的存在是用空间交换时间的技术，物化视图的个数是受到约束的。

（2）维护代价：即当原始数据库中的数据发生变化时，物化视图作为实际存在的数据，也是需要同步更新来保持数据一致。对于较大的数据仓库来说，更新数据的耗时会比较长，如果与之相关的物化视图比较多，那么更新的代价就很大，这时需要减少物化视图的数量以得到平衡。对于空间限制比较宽松的情况，物化视图过多的话会影响到更新时的速度，所以如何寻找平衡点也是物化视图选择中一个重要的考虑因素。

（3）物化视图带来的收益：指不生成某个物化视图和生成此物化视图对查询速度的贡献，对于生成了物化视图的情况，相应的查询可以直接得到结果，未生成物化视图的查询时间计算需要考虑到选择、连接、聚集等几个方面的运算速度。收益分为相对收益和绝对收益，相对收益是生成物化视图对现有视图集的效率改进。而绝对收益就是物化视图对原始数据集的效率改进。一般进行收益计算时，采用的是相对收益，其更能反映实际的收益效果。

本文采用的方式是定期更新与根据查询效率更新相结合的方式，一方面对每次查询请求判断是否生成相应的物化视图，通过一个阈值来作为是否生成的评判标准；另一方面设定一个固定时间进行全局性的物化视图集的更新，主要是按照每个物化视图集的权重进行排序并将靠前的物化视图生成。当然已经存在的不需要生成，只需要生成那些新出现的物化视图。

3 数据立方体格结构图

对于物化视图，每种维度有聚集和不聚集两种选择，共有2＾n个可能的物化视图。如果一个物化视图A的所有维度都在另一个物化视图B中出现，即B将数据集划分得更为精细，同时划分方式是包括A的所有划分方式的，此时B和A是一种偏序关系，记做A≦B，所有的可以由A计算的查询都可以由B来计算得到。对于物化视图的集合｛V1，V2，V3……Vn｝，它们之间以视图之间的偏序关系作为箭头，视图本身作为结点形成的图就叫做数据立方体的格图。

例如，对一个有4个维度的数据集，4个维度分别为部门（A），科目（B），项目（C），年份（D），那么其可能的物化视图共有2＾4＝16个，按照维度数量可以分组如下：

（1）（A，B，C，D），即数据集本身

（2）（A，B，C），（A，B，D），（A，C，D），（B，C，D）

（3）（A，B），（A，C），（A，D），（B，C），（B，D），（C，D）

（4）（A），（B），（C），（D）

（5）none，即不划分的数据

这些物化视图按照维度的包含关系可以生成格结构图，维度的包含关系也表明了对于相应查询的包含关系，即若一个物化视图是包含另一个的，那么它可以进行另一个物化视图能够进行的所有查询。上面的物化视图集能够形成的数据立方体格结构图如图1所示。

其中的边是从上往下的单向边，上面是父结点，下面是子结点，每个结点表示一个物化视图，结点的内容即物化视图中包含的维度。例如（A，B）表示按照部门和科目分类形成的物化视图。（A，B，C，D），（A，B，C），（A，B，D）都存在流向（A，B）的通路，表明（A，B）这一物化视图可以被它们生成，能从（A，B）得到结果的查询都可以从上面3个物化视图中任意一个通过聚集计算得到。

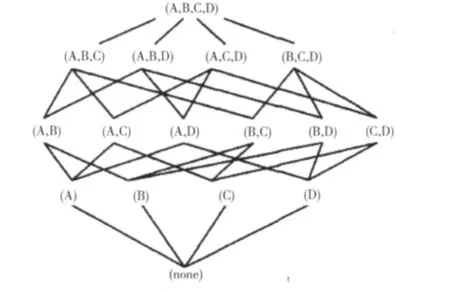
图1 数据立方体格结构

4 BWCC权重及相对收益计算模型

本文采用基于用户查询习惯和物化视图加权相对收益的动态选择算法。其考虑了视图的大小，视图的相对收益，另外还考虑了物化视图所包含的每项属性的权重，即特定的某项维度被查询的可能性，另外系统根据用户的查询输入进行学习，根据查询频率动态调整，保持提供最适合的物化视图选择方案。

影响选择方案的核心因素有几个：查询频率，特定维度的权重，视图大小以及物化视图带来的相对收益。用Vq来表示视图q的价值，并采用查询驱动机制，每次查询涉及到的视图的价值相应增大，不定期地更新物化视图以满足不断变化的查询需求。

（1）维度权重用来表示每项维度被查询到的可能性的大小，初始化均为1，可由用户自行定义更改，对于特定的物化视图q，其维度权重Weight（q）为所有维度项权重的平均值。

（2）物化视图q的相对收益Ben（q）表示物化视图q给已有的物化视图集带来的查询效率的改进，B（q，s）＝∑v≤qBv，其中v为在格结构图中q的子结点，Bv为q对于v带来的查询效率的改进。定义w为v的父结点中已经生成物化视图并且具有最少的元组数的节点，如果C（v）＜C（w），则Bv＝C（w）－C（v），否则Bv＝0。

（3）查询频率Count（q）表示视图q被查询到的次数，每个查询都可以对应到与查询条件含有同样维度条件的物化视图q。

（4）物化视图q的占用空间的大小是衡量其价值的另一因素，其与物化视图包含的元组数C（q）成正比，在计算价值时可以直接用C（q）表示。对于具有一定稀疏度的多维数据集，实际生成的物化视图尺寸往往会小一些。假定原始多维数据集的稀疏度为k，物化视图较原数据集对n个维度进行了聚集，每个维度包含的属性项数为d1，d2，……dn，原始数据集元组数量为a，则新物化视图的元组数量C（q）估计值为

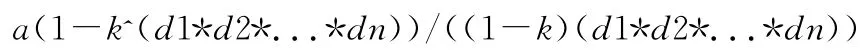
本文采用的算法对物化视图价值Value（q）计算的公式 为Value（q）＝Ben（q）＊Weight（q）＊Count（q）2／C（q）。从上式可以看出，本文的算法中物化视图q的价值Value（q）与其相对收益Ben（q）和视图权重Weight（q）成正比，收益和维度权重越大，视图价值越高；Value（q）与查询到的次数Count（q）的平方成正比，查询到的次数越多，视图价值越高，同时在一段时间内查询到的次数越多，价值增长越快；Value（q）与视图的元组数个数成反比，表示视图越大，占用空间越多，其价值越低。

5 BWCC算法实现

在借鉴已有的算法基础上，本文给出了基于查询习惯和加权相对收益的动态选择及调整算法，算法的流程图如图2所示。

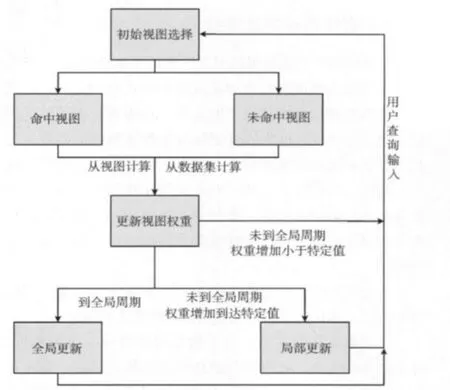
图2 BWCC算法流程

对于物化视图的初始选择，可以由用户指定，也可以由系统根据设置的维度权重和视图占用空间大小进行自行选择，算法具体描述如下：

算法1：初始选择物化视图集算法

输入：空间限制S，视图集V

输出：物化视图集MV

／／初始化视图集V中每个视图q的价值Value＿begin（q）

for each q in V

Value＿begin（q）＝Weight（q）／Size（q）；

对所有q按照Value＿begin（q）从大到小进行排序；

while（S＞0）｛

for each q in V｛／／遍历视图集

／／选择视图加入物化视图集

if（S－Size（q）＞0）｛

MV＝MV＋ ｛q｝；／／将视图q加入物化视图集

S＝S－Size（q）；／／减少剩余空间

｝｝｝

return MV；

对于物化视图的初始选择，可以由用户指定，也可以由系统根据设置的维度权重和视图占用空间大小进行自行选择，Size（q）表示物化视图q占用的空间大小，初始时的视图价值是通过该视图所包含的维度权重的平均数以及视图大小综合考虑的。维度权重的平均数越大，视图包含的维度越容易被查询到，其价值就越高，而视图的占用空间越大，其价值就越低。

随着用户查询的输入，算法会根据查询的频率调整各个视图的价值，并判断是否需要进行物化视图集的局部更新和全局更新。对于查询输入a，视图调整的算法步骤如下：

算法2：物化视图集调整算法

输入：查询a，物化视图集MV

输出：物化视图集MV

if（MV中存在视图q，a对应的视图＜＝q，且C（q）最小）｛

由q来回答a；

｝

else从原始多维数据集聚集计算回答a；

Count（q）＋＋；／／a对应的视图计数增加

Value（q）＝Ben（q）＊ Weight（q）＊ Count（q）＊Count（q）／C（q）；／／更新视图q的价值

Count＿all＋＋；／／全局更新计数增加

／／当查询未命中而且q价值增加较多时，调用局部更新的算法

if（Count＿all＜time ＆ ＆ 查询未命中 ＆ ＆ Value（q）－Value＿old（q）＞val）｛

调用局部更新的算法；

｝

else｛调用全局更新算法；｝

Return MV；

每次查询时，都会对相对应的视图的计数进行增加，不断更新视图的价值。更新后会计算视图新的价值与旧的价值之差，当差值高于一定值时，说明此视图最近比较常用，并且在这段时间内可能会经常用到，需要进行物化，以便提高之后的查询效率和命中率。视图局部更新的方法为先判断当前空间限制是否足够容纳q，如果不足，则删去价值最小的视图，直到空间足够，最后将q加入物化视图集。

算法3：物化视图集局部更新算法

输入：查询对应的视图q，物化视图集MV，空间限制S

输出：物化视图集MV

if（S－Size（q）＞0）｛／／剩余空间满足条件时，直接添加q进入物化视图集

MV＝MV＋ ｛q｝；／／添加q到物化视图集

S＝S－Size（q）；／／更新空间限制

｝else｛

／／空间不够时，删除物化视图以腾出空间

while（S－Size（q）＜0）｛

获得价值最小的物化视图q′

MV＝MV－q′；／／将其删除

S＝S＋Size（q′）；／／更新空间限制

｝

MV＝MV＋ ｛q｝；／／添加q到物化视图集

S＝S－Size（q）；／／更新空间限制

｝

return MV；

当过了一定长度的时间后，用户的习惯可能已经发生了变化，此时需要对物化视图进行全局的更新，利用历史价值信息以及视图本身的价值进行综合判断，选择合适的视图进行物化完成全局更新的操作。全局更新的方法与初始选择类似，不同的是对于视图价值的计算，全局更新是对当前视图价值乘以历史系数Value（q）＝Value（q）＊v＿his，其值在0到1之间，可以参考用户习惯的延续性进行设定。

算法4：物化视图集全局更新算法

输入：物化视图集MV，空间限制S，历史系数v＿his

输出：物化视图集MV

／／对V中每个视图q计算价值

for each q in V｛

Value（q）＝Value（q）＊v＿his；／／计算时乘以历史系数v＿his

Value＿old（q）＝Value（q）；／／更新 Value＿old的值

Count（q）＝0；／／清零查询计数

｝

对V中的所有视图按照价值从大到小进行排序；

／／从大到小加入物化视图集

While（S＞0）｛

for（each q in V）｛

if（S－Size（q）＞0）｛／／空间足够时添加q到物化视图集

MV＝MV＋ ｛q｝；／／加入物化视图集

S＝S－Size（q）；／／更新空间限制

｝｝｝

return MV；

本文中的BWCC算法的在初始选择时的复杂度是O（nlogn），与排序算法相同。在系统运行过程中，随着用户查询的到来，还会进行局部更新和全局更新，局部更新的时间复杂度与视图数量无关，耗时较少；全局更新的时间复杂度和初始选择相同，也是O（nlogn）。

6 实验分析

本文将BWCC算法与贪心算法和排序算法进行对比，分析了其时间复杂度，测试了其查询命中率和总体收益。本文在CPU 类型为 Genuine Intel（R）T2050 1.60GHz，1.60GHz的计算机中进行测试，测试对象为一个维度层次项个数为10，每项对应的属性值个数为5，事实项个数为2的多维数据集，空间限制为10%。

测试分为两组数据进行，第一组数据为完全随机生成的1000个查询，每个维度属性在查询中出现的概率相同，均为0.5。第二组分为3个阶段，每阶段1000个查询，并让其中指定的10个维度属性在查询中出现的概率增至0.8，其余40个维度属性的出现概率更改为0.2。对于不同的阶段，更换指定的10个维度，用以表现用户习惯的历史延续性。

第一组查询命中率比较如图3所示。

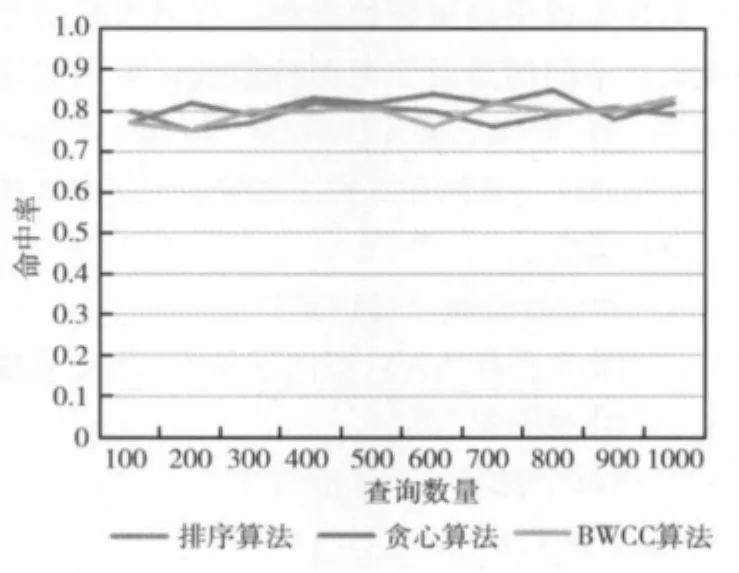
图3 第一组查询命中率比较

对于第一组查询，由于查询是完全随机的，所以3种算法在命中率上差别并不大。对于静态的贪心算法和排序算法来讲，在初始选择物化视图集后就不作变化，其命中率也只和初始的选择有关。对于BWCC算法，它的动态调整机制对于完全随机的查询没有意义，其初始选择算法和排序算法相同，也是按照尺寸大小进行排序，因此其命中率也和排序算法接近。总体来讲，3种算法在对于完全随机的用户查询，其命中率是大体接近的。

第二组查询命中率比较如图4所示。

对于具有一定规律的用户查询，查询的结果走势大致分为三段，每段对应1000个查询。对于贪心算法和排序算法来说，物化视图在初始确定之后就不变了，命中率取决于被赋予高出现概率的维度属性是否有其物化视图在初始时被生成。排序算法和贪心算法的命中率随着维度属性出现概率的分布变化而变化，时高时低，呈现随波逐流的态势，而不能保持一个相对稳定的命中率。

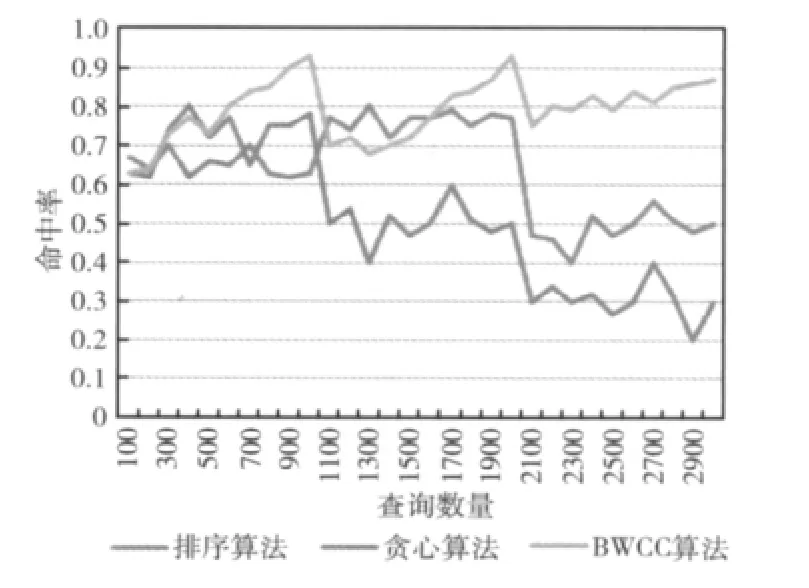
图4 第二组查询命中率比较

对于BWCC算法，在上面的实验中，大体分为3个阶段。每个阶段的命中率都是开始较低，而后逐渐升高。逐渐升高的原因是它随着用户查询不断调整自己的物化视图集。而每当查询偏好变化时，由于其之前生成的物化视图集与新的查询习惯不一定匹配，所以命中率会出现一定的下降，随着时间的推移，其自我调整的机制又将命中率不断提高。可以看出，针对这种有一定侧重的查询集合，BWCC算法的命中率要高于贪心算法和排序算法，对于查询偏好的变更也有较好的处理能力，本文中的BWCC算法在命中率上具有较大优势。

7 结束语

本文对数据仓库系统中的物化视图选择问题进行了研究，提出了基于习惯和加权相对收益的动态选择及调整算法BWCC，此算法考虑了视图的相对收益、视图尺寸、维属性权重以及用户查询习惯，可以根据查询的偏好进行动态的调整，提高了命中率。另外用户也可以给不同的维度属性赋予不同的权重来表示其被查询到的可能性大小，权重也会影响到系统对于物化视图集的选择，可以更好地对用户偏好做出改变。总体来说，这一算法的命中率高于传统选择算法，还可以根据用户习惯进行动态调整，时间复杂度与传统选择算法差别不大，相对于传统算法有较大的优势。

［1］PMark Whitehorn，PRobert Zare，Mosha Pazusmansky.Problem solving for MDX for SQL Server 2005［M］.New York：Springer－Verlag，2007：105－131.

［2］LI Caihua.Application of OLAP technology in production evaluation［J］.Computing Technology and Automation，2009，28（4）：133－137（in Chinese）.［李才华.OLAP技术在生产评价中的应用［J］.计算技术与自动化，2009，28（4）：133－137.］

［3］LAN Jian，JIN Hongmei.The design and realization of OLAP based data warehouse analysis model in enterprises［J］.Process Automation Instrumentation，2006，27（5）：9－12（in Chinese）.［蓝箭，金红梅.基于OLAP的企业数据仓库分析模型设计与实现［J］.自动化仪表，2006，27（5）：9－12.］

［4］CHEN Qimai，HE Chaobo，LIU Hai.OLAP－based collaborative educational decision［J］.Computer Applications，2009，29（1）：304－305（in Chinese）.［陈启买，贺超波，刘海.基于OLAP的高校教学协同决策［J］.计算机应用，2009，29（1）：304－305.］

［5］Themis Palpanas，Nick Koudas，Alberto O Mendelzon.On space constrained set selection problems［M］.England：Data Knowl，2008：200－218.

［6］JIANG Nan，GAO Wei，ZHANG Liqiu.Research and application of data mining model based on analysis services［J］.Machinery Design ＆ Manufacture，2007（4）：83－85（in Chi－nese）.［姜楠，高巍，张丽秋.基于Analysis Services的数据挖掘模型的研究与应用［J］.机械设计与制造，2007（4）：83－85.］

［7］Kobra Etminani，Prof M Naghibzadeh.A min－min max－min selective algorithm for grid task scheduling［C］／／Uzbekistan：3rd IEEE／IFIP International Conference in Central Asia，2007：1－7.

［8］Dong F，Akl S G.Scheduling algorithms for grid computing：state of the art and open problems［R］.Technical Report，2006.

［9］Tang Zhaohui，Jamie MacLennan.Data mining with SQL server 2005［M］.Beijing：Tsinghua University Press，2007：45－53（in Chinese）.［Tang Zhaohui，Jamie MacLennan.Data mining with SQL server 2005［M］.北京：清华大学出版社，2007：45－53.］

［10］Gupta H，Mumick I S.Selection of views to materialize under a maintenance cost constraint［C］／／ICDT，1999：453－470.