矿热炉内镍铁还原过程电流密度分布与温度场的有限元分析
2013-11-28王子坤李拓文李宝宽
王子坤,李拓文,李宝宽
(1.东北大学 材料与冶金学院,沈阳 110819;2.沈阳市民营科技机构协调服务中心,沈阳 110003)
目前,世界范围内的红土镍矿火法冶炼主流 工艺是:回转窑焙烧—电炉熔炼,即RKEF法[1].矿热电炉靠电极的埋弧电热和物料的电阻电热来熔炼物料,如图1所示,其间包含一系列物理化学现象,包括多相流、高温还原反应、电弧电能的转化与传导等.为使设计者结合生产实际,达到最佳炉况的匹配参数,为使冶炼操作者更清楚地了解炉况,更得心应手地操作,以达到节能的目的,分析矿热炉内交流电变化及作用规律以及温度场分布非常必要.

图1 矿热炉炉内剖面示意图Fig.1 Schematic diagram of submerged arc furnace[2]
目前国内外使用数值模拟手段研究矿热炉还原熔炼过程,特别是熔炼镍铁的文献较少.由于镍铁矿热炉属于多渣操作,硅铁等少渣操作矿热炉模拟对镍铁生产指导意义不大.储少军等用数值模拟方法对硅钙矿热炉进行了一些研究[3~4],然而只建立了出铁口的三维模型,并未对炉内过程建立三维有限元模型;Kadkhodabeigi等[5]采用多相流模型研究了硅铁矿热炉的出铁过程,温度为常数作为已知条件,并没有分析炉内温度场分布.王振等使用有限元模型研究了矿热炉制备单晶氧化镁炉内温度场[6],着重研究了电极、电弧、料层及产品区域,但完全没有考虑渣层的影响,没有研究交流电的行为.Scheepers等建立CFD模型全面分析了矿热炉生产磷铁的温度场与还原率[7~9],但电弧与坩埚区域仅当作圆柱处理,关键部位建模过于简化,并且也没有研究炉内交流电行为.
本文基于电磁场和传热学的基本理论,建立镍铁矿热炉炉体内部电磁场和温度场的数学模型,以镍铁矿热炉中料层、渣层、坩埚层和液态镍铁合金整体系统为研究对象,进行一体化有限元分析.鉴于料层中的坩埚区对熔炼过程有重要影响,在炉体建模时,建立比圆柱形更复杂的碗型坩埚区模型,采用结构化网格,使计算结果更接近生产实际.先计算矿热炉系统中电流密度和焦耳热的分布,并着重分析炉内电流密度分布规律,再利用有限元的热电耦合计算得到系统内的温度分布.通过改变矿热炉炉体设计中的经验系数,控制原始模型的单一几何尺寸作为变量,分别改变电极直径、电极中心距以及炉膛高度等参数,研究不同炉体参数对系统内温度场分布的影响.
1 模型建立
1.1 数学模型
使用磁矢量法,麦克斯韦基本方程组与导出方程是电磁场的基本点也是出发点.电磁场满足Maxwell方程组:




式中:Q为焦耳热;σ为电导率;ε为介电常数;μ 为磁导率为热功率密度.
计算过程中作如下假设[10]:
(1)埋弧电炉炉内温度远远超过居里点,设定电极与熔池各层的相对磁导率均为1.
(2)假设料层及金属等有关物性参数可视为常数,且具有均匀性和各向同性.
(3)忽略电炉系统内的接触电阻.
(4)假设电极与料层、渣层和镍铁层保持相对静止.
根据导热微分方程整理,可得到柱坐标下热传导控制方程表示为

其中,T表示温度;t为时间;λ为热传导系数;r为径向坐标;z为轴向坐标;ρ为材料密度;cp表示材料比热容;q表示内热源;ξ为材料相变潜热项.
由于工艺使用的埋弧电炉为固定封闭式,温度场施加的边界条件以第一类边界条件和第三类边界条件为主.电极顶端施加第一类边界条件,为

由于冷却系统的作用,炉壁四周施加第三类边界条件,表示为

料层顶端按第三类边界条件处理.因为同时进行对流和辐射换热,将辐射项转化到复合传热系数中,有

埋弧电炉底端采用第二类边界条件,绝热底面.

1.2 计算方法与边界条件
选用磁矢量位方法(Solid97单元)求解电磁场和焦耳热场.首先由矢量磁位计算出磁感应强度、电流密度和电磁力,然后将电流密度结果代入Joule定律公式,通过耦合求解得到热功率密度(焦耳热)分布.再转换单元(使用Solid70),对温度场进行求解计算[11].
电极、物料、渣层和镍铁层选择时间积分电势(volt)作为自由度.磁场计算边界条件为,有效功率12 000 kW时进行设计计算得到的二次电流[12],为23 277.9 A,并耦合 volt自由度;以120(°)相位施加交流电流,如图2;铁锭下端面电位设为0;空气外表面处设置磁平行边界条件.物性参数与操作参数见表1.

图2 加载交流电流相位示意图Fig.2 Loaded AC phasic diagram

表1 镍铁矿热炉物性参数与操作参数Table 1 Physical property and operation parameter for ferronickel ore smelter
1.3 模型建立与网格划分
矿热炉炉体参数的计算方法主要有两类,一类是安德烈-米库林斯基方法[13,14],一类是威斯特里 - 斯特隆斯基方法[15~17].根据研究,安德烈-米库林斯基方法是基于电极直径的方法,威斯特里-斯特隆斯基方法是基于功率密度的方法[18].由于电极直径与功率密度的计算都是电流的函数,所以归根到底,两者都是基于电流的方法,只是指数倍数不同.
根据目前生产现场中广泛使用的镍铁矿热炉炉型,建立几何参数如表2的镍铁矿热炉1号模型.以1号模型为基础,通过改变单一变量,再建立六个不同几何参数的模型.不同模型的控制变量参数按照表3设置,再根据熔池深度与电极直径的经验关系、物料平衡计算出的铁渣比以及炉内电阻计算出各层厚度[19].
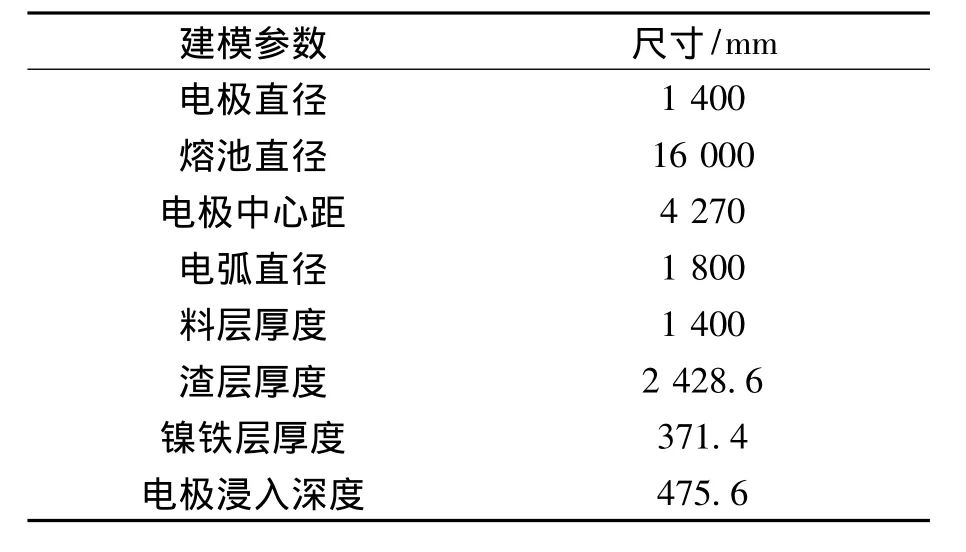
表2 镍铁矿热炉1号模型主要几何参数Table 2 No.1 ferronickel ore smelter main geometric parameter
由SolidWorks软件进行模型建立,导入ANSYS软件进行网格划分.电弧按等效电阻处理,坩埚区域建模如图3所示.由于坩埚区为矿热炉生产主要产热区域,对温度场分布影响较大,所以本文比前人细化了坩埚区域建模.采用手动控制单元大小,七个模型的单元长度皆为0.3 m,渣层和镍铁层等主要计算区域为结构化网格;坩埚区(电弧)、料层以及空气为非结构化网格.从表3中可以看出,不同模型的单元数相近.

图3 模型网格划分情况Fig.3 The mesh of model
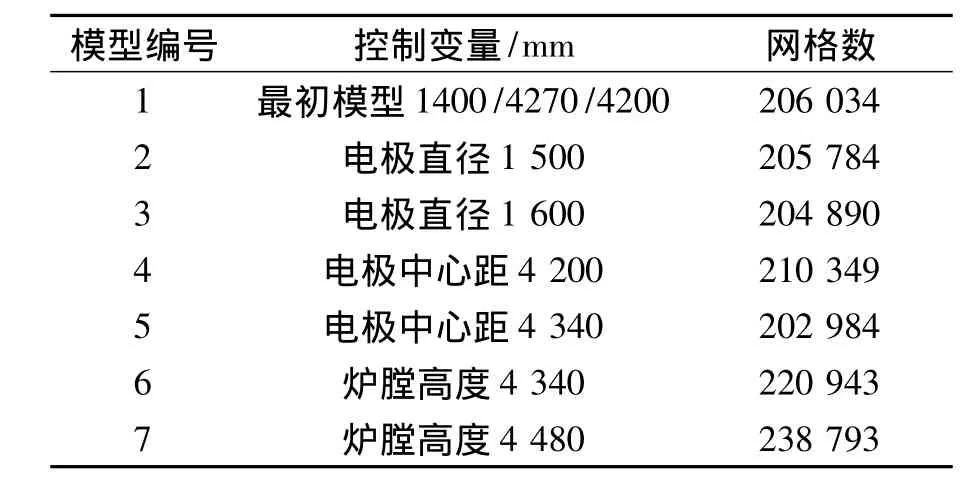
表3 不同镍铁矿热炉模型参数变化与网格数Table 3 Grid numbers of ferronickel ore smelter geometric parameters
2 结果与讨论
2.1 电流密度分布
由图4可以看出,电流由一根电极流入,另两根电极流出.由于电极四周多孔料层电阻率较高,所以通过自焙电极侧壁流入料层的电流极少.电极底部压降很大,所以电流主要以电弧形式从电极底端流出,呈四周发散状.电流使气体电离,电阻率减小.由于料层和渣层的电导率较低,进入料层和渣层后电流密度发生改变.不过渣层电导率高于料层电导率,所以向下通过电弧流入渣层的电流密度要多于向四周通过料层的电流密度.渣层中电流重新分布,方向从流入电极指向流出电极.
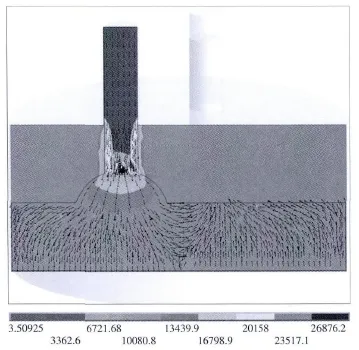
图4 电流密度计算结果Fig.4 Calculated results for current density
2.2 焦耳热场计算结果
如图5所示,在埋弧电炉中,产热部位主要是电弧,料层主要起到保温、减少噪声和形成坩埚区的作用.由于料层和渣层的电阻率较高,在大电流通入时也会产生较多热量,所以焦耳热(热功率密度)最大值出现在电弧与电弧附近的料层渣层交界面处.巨大的电热在熔化物料的同时,使中心区域达到氧化亚铁的还原温度,反应生产的气体在料层的压力下形成坩埚区.

图5 焦耳热计算结果Fig.5 Calculated results for Joule heat
2.3 温度场计算结果
埋弧电炉内最高温度在电弧及电弧附近坩埚区,最高温度达到1 885℃.自焙电极底部中心区域由于燃弧,温度最高,电极消耗速度更快,所以电极底部常形成“凹坑”.热量从坩埚区向四周扩散.3个产热区域同时向中心区域大量传热,使其温度较高,温度相对均匀.料层径向从坩埚区到炉壁温度场分布呈下降趋势,温度梯度非常大;渣内纵向炉温分层均匀,温度场分布呈下降趋势,考虑到液态镍铁合金内部强烈的对流传热,渣层内部纵向温度梯度大于径向温度梯度.由于液态镍铁水的导热系数要远远高于渣的导热系数,所以热量在镍铁层扩散速度快,温度分布较为均匀,数值处于1 550℃左右.

图6 温度场计算结果Fig.6 Calculated results for temperature field
2.4 不同建模参数下温度场对比
电极直径对温度场的影响结果对比如图7所示.由于安德烈-米库林斯基方法是基于电极直径的方法,电极直径的变化对温度场的影响较大.从图7中可以明显地看出,随电极直径增大,高温区域减小,温度降低.原因是在通入同样大小的电流时,电极直径大时电流分散更为均匀,接触截面积大,热量分布较为均匀.
电极直径对镍铁层表面温度场影响对比如图8所示.镍铁层表面温度场结果与总的温度场结果相似,电极增大,高温区域减小,温度降低.由于不同电极直径对几何参数尤其是渣层和镍铁层高度影响较多,镍铁产品层温度变化较大.电极直径对渣层表面温度场影响对比如图9所示.渣层表面温度场结果与总的温度场结果相似,电极增大,最高温度区域减小,温度降低.
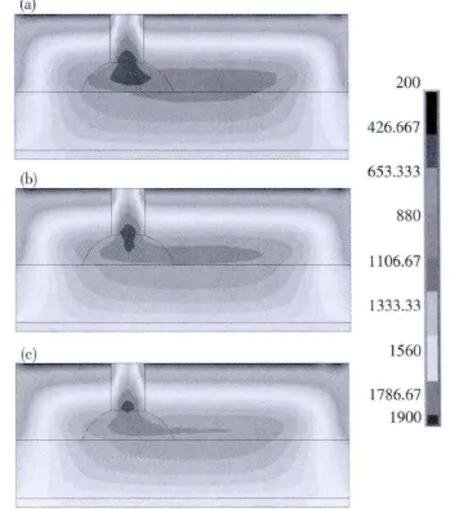
图7 不同电极直径下的温度场结果对比Fig.7 Temperature fields for different electrode diameters
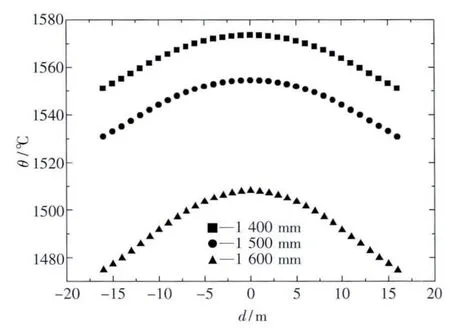
图8 电极直径对镍铁层表面温度的影响Fig.8 Influence of electrode diameters on temperature field on ferronickel surface
由此可见,电极直径越小,炉内温度越高.但考虑到电极承载电流能力的因素,电极直径不能过小,否则可能造成电极事故.使用安德烈-米库林斯基电炉设计方法时,镍铁电炉推荐的电流密度为 3.0 ~3.5 A/cm2[12].

图9 电极直径对渣层表面温度的影响Fig.9 Influence of electrode diameters on temperature field on slag surface
电极极心距对温度场影响的对比如图10所示.可以看出,电极极心距对温度场的影响并不像电极直径那样呈单向关系,而是存在一个最佳值.当电极极心距较小时,温度过于集中在中间区域,热量分布不均;当电极极心距较大时,热量散失较多,热效率低;当电极极心距适当时,热量利用率最高.从图 10中可以看出,电极极心距为4 270 mm的情况下比较适当.

图10 不同电极中心距下的温度场结果对比Fig.10 Temperature fields for different electrode center diameters

图11 电极中心距对镍铁层表面温度的影响Fig.11 Influence of electrode center diameters on temperature field on ferronickel surface
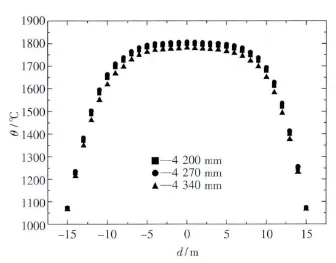
图12 电极中心距对渣层表面温度的影响Fig.12 Influence of electrode center diameters on temperature field on slag surface
电极极心距对镍铁层表面温度场影响对比如图11所示.镍铁层表面温度场结果与总的温度场结果相似,当处于最佳极心距位置,即4 270 mm时,传导到镍铁层的热量较多,温度较高.电极极心距对渣层表面温度场影响对比如图12所示.渣层表面温度场结果与总的温度场结果相似,在电极极心距较小时,平均温度高;在电极极心距较大时,平均温度低.电极极心距适当时,高温区面积最大.
由此可见,电极中心距与炉温不是单向关系,而是存在一个最佳值,使炉内平均温度达到最高.
炉膛高度对温度场影响对比如图13所示.可以看出,炉膛高度对温度场的影响像电极直径一样呈单向关系.炉膛高度越高,高温区面积小,平均温度越低,热量分布不均;当炉膛高度适当时,热量集中较多,散热较少,温度较高.
炉膛高度对镍铁层表面温度场影响对比如图14所示.镍铁层表面温度场结果与总的温度场结果相似,炉膛越高,最高温度区域减小,温度降低.不过由于不同炉膛高度对几何参数尤其是渣层和镍铁层高度影响较多,镍铁产品层温度变化较大.炉膛高度4 480 mm时,传导到镍铁层的热量较少,温度较低,降到1 500℃以下.炉膛高度对渣层表面温度场影响对比如图15所示.渣层表面温度场结果与总的温度场结果相似,炉膛高度对渣面温度场分布影响不大.不过由于高度越高,炉子体积越大,传热越多,核心区域温度越低.
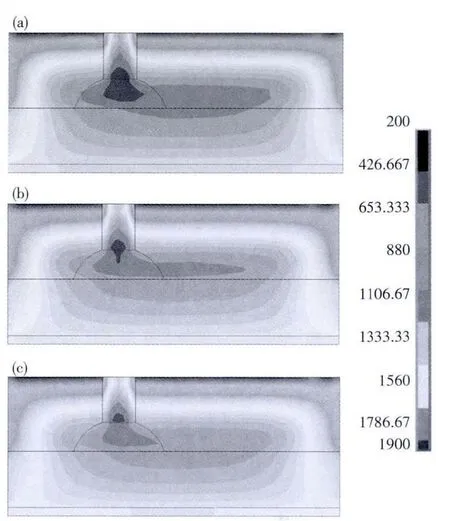
图13 不同炉膛高度温度场结果对比Fig.13 Temperature fields for different furnace heights

图14 炉膛高度对镍铁层表面温度的影响Fig.14 Influence of furnace height on temperature field on ferronickel surface

图15 炉膛高度对渣层表面温度的影响Fig.15 Influence of furnace height on temperature field on slag surface
由此可见,炉膛高度越小,炉内温度越高.但产量因素也对炉型体积大小有所影响,因而炉膛高度也不能过小.使用安德烈-米库林斯基电炉设计方法时,镍铁电炉推荐的炉膛深度系数为2.8 ~ 3.1[12].
3 结论
本文对多渣镍铁还原矿热炉一体化系统进行有限元分析.建立碗型坩埚区模型使计算结果更接近生产实际.通过对电流密度、焦耳热密度和温度场分布的分析,得到了以下结论:
(1)电流密度在电极、电弧和坩埚区域较大,流入料层中的电流很少;电流流入渣层时成发散状,电流密度减小并重新分布;流入产品层中电流非常少.
(2)热量主要在电弧和料层渣层交界处产生.电极底端坩埚区温度最高,炉内其余部分温度场呈层状递减分布:料层内温度梯度最大;料渣交界面处,中心坩埚区域温度均匀,坩埚区以外温度梯度很大;渣层内温度梯度比料层内温度梯度稍小,渣层中的纵向温度梯度明显大于径向温度梯度.产品层内温度分布较为均匀.
(3)电极直径、炉膛高度与炉内平均温度成单向关系,即电极直径越小、炉膛高度越小,炉温更高.由于受电极承载电流能力因素制约,电极直径不能无限减小;炉体高度的决定也要考虑产量因素.电极中心距与炉温不是单向关系,而是存在一个最佳值,使炉内平均温度达到最高.
[1]秦丽娟,赵景富,孙镇,等.镍红土矿 RKEF法工艺进展[J].有色矿冶,2012,28(2):34-36.
(Qin Lijuan,Zhao Jingfu,Sun Zhen,et al.Nickel laterite rotary kiln - electric furnace process and development[J].Non- Ferrous Mining and Metallurgy,2012,28(2):34-36.)
[2]Kadkhodabeigi M,Tveit H,Johansen S T.Modeling the tapping of silicon melt from the submerged arc furnace[C]//Seventh International Conference on CFD in the Minerals and Process Industries.2009.
[3]胡冬,储少军,李忠思,等.ANSYS软件在矿热炉水冷出铁口设计中的应用[J].铁合金,2011,42(2):31-35.
(Hu Dong,Chu Shaojun,Li Zhongsi.Application of ANSYS in the design of water-cooled tapping hole of submerged arc furnace[J].Ferro - Alloys,2011,42(2):31 -35.)
[4]储少军,郭映波,王玉刚,等.硅钙合金生产过程的-维动态模型[J].铁合金,2003(3):1-6.
(Chu Shaojun,Guo Yingbo,Wang Yugang,et al.An unidimensional dynamic Model for the silicocalcium process[J].Ferro -Alloys,2003(3):1 -6.)
[5]Kadkhodabeigi M,Tveit H,Johansen S T.Modelling the tapping process in submerged arc furnaces used in high silicon alloys production[J].ISIJ international,2011,51(2):193 -202.
[6]Wang Z,Wang N H,Li T.Transient 3D simulation of a submerged-arc furnace for production of MgO single crystal[C]//Materials Science Forum,2011,675:995-998.
[7] Scheepers E,Yang Y,Reuter M A,et al.A dynamic-CFD hybrid model of a submerged arc furnace for phosphorus production[J].Minerals engineering,2006,19(3):309-317.
[8] Scheepers E,Adema A T,Yang Y,et al.The development of a CFD model of a submerged arc furnace for phosphorus production[J].Minerals engineering,2006,19(10):1115 -1125.
[9] Scheepers E,Yang Y,Adema A T,et al.Process modeling and optimization of a submerged arc furnace for phosphorus production[J].Metallurgical and Materials Transactions B,2010,41(5):990-1005.
[10] Alghisi D,Milano M,Pazienza L.From ESR to continuous CC-ESRR process:development in remelting technology towards better products and productivity[J].Metallurgia Italiana,2005,97(1):21 -32.
[11]王芳,李宝宽.电渣重熔过程中的电磁场和 Joule热分析[J].金属学报,2010,46(7):794-799.
(Wang Fang,Li Baokuan.Analysis of electromagnetic field and Joule heating of electroslag remelting processes[J].Acta Metallurgica Sinica,2010,46(7):794 -799.)
[12]栾心汉,唐琳,李小明,等.镍铁冶金技术及设备[M].北京:冶金工业出版社 ,2010:141-143.
(Luan Xinhan,Tang Lin,Li Xiaoming,et al.Ferronickel metallurgy technology and equipment[M]. Beijing:Metallurgical Industry Press,2010:141 -143.)
[13] Andreae F V.Design and control of ferroalloy furnaces[J].Electrical Engineering,1950,69(6):531-531.
[14] Микулинский А С.Определение параметров руднотермиче- ских печей на основе теории подобия[J].М - Л:Энергия,1964,87 с:1964.
[15] Westly J.Critical parameters in design and operation of the submerged arc furnace[C]//Proceedings of the 33rd Electric Furnace Conference.Iron and Steel Society,Warrendale,USA.1975:47-53.
[16] Westly J.Resistance and heat distribution in a submerged-arc furnace[C]//Proceedings of INFACON 74.South African Institute of Mining and Metallurgy,Johannesburg.1975,121-127,1975.
[17] Струнский Б М.Руднотермические плавильные печи[J].М:Металлургия,1972.
[18]李蒙姬,张烽.硅铁电炉的电气参数与电炉几何参数的确定[J].铁合金,2005(1):9-11.
(Li Mengji, Zhang Feng. Determination of electric and geometric parameters of ferrosilicon furnace[J].Ferro -Alloys,2005(1):9 -11.)
[19]郭茂先.工业电炉[M].北京:冶金工业出版社,2002:105-116.
(Guo Maoxian.Industrial furnace[M].Beijing:Metallurgical Industry Press,2002:105 -116.)
