简单雷达目标空域瞬态极化特性研究*
2013-11-28黄双华
郭 凯 黄双华 刘 涛
(海军工程大学 武汉 430033)
1 引言
极化是电磁波矢量属性的一种体现,不同目标对极化波的散射特性与目标的形状、材料、空间位置分布、运动状态以及入射电磁波的频率都有密切的关系。目标散射中心模型是空域雷达目标极化特性研究的理论基础。本文从最简单的雷达目标(两点散射模型)出发,利用几何绕射理论(GTD模型)建立了极化宽带散射模型,分析了模型的极化散射特性随入射电磁波频率以及空间姿态敏感变化的规律,并用MOM方法进行了仿真,验证了我们结论的正确性,并分析了简单雷达目标的动态散射特性。对于其他复杂目标,都可以利用电磁计算矩量方法验证此理论推导的正确性。
2 简单雷达目标空域瞬态极化特性分析
2.1 基于GTD模型的极化散射中心模型
本文主要考虑散射中心之间的相对位移关系对后向散射矩阵特征的影响,故暂不考虑散射中心自身姿态与电磁波入射方向的相对角度引起的变化,也就是说,在电磁波入射过程中(实际一般是小角度范围的电磁波方向变化),散射中心的散射矩阵与电磁波入射方向是无关的。在最简单的两点模型中,我们将两点的散射矩阵分别记为S1,S2,因为散射矩阵与雷达目标的距离以及入射电磁波频率等因素有关,为了能够统一地表征目标的散射特性,我们将它们的散射矩阵归一化(可以令散射矩阵元素的平方和为1,这样相同散射机理的散射矩阵的归一化散射矩阵只差一个绝对相位),记为

这样,我们就建立了两点散射中心目标的极化散射模型,如图1所示。图1中O为雷达位置,在此使用雷达坐标系。横坐标为X,纵坐标为Y。图中两圆点A,B为两个点目标,所示的雷达视线与AB的交点为目标的重心C,这里也设为雷达回波的零相位参考点。目标的法线方向为CD,目标长度为L。雷达到目标重心的距离为R0,雷达到两个散射中心的距离为Rm,m=1,2。入射电场为图OC所示方向,定义雷达发射电磁波与目标法线的夹角为θ=∠OCD。

图1 雷达目标的两点散射模型


2.2 复杂目标的散射矩阵描述

其中Ei、分别为第m个散射中心的入射电场强度和散射电场强度,m为散射中心,且m=1、2,Snm为第m 个散射中心的归一化散射矩阵,f为入射电磁波频率,f0为中心频率,也是一个强度参考基准频率,αm为第m个散射中心的类型参数,Am为第m个散射中心在中心频率f0上的散射系数
由式(2)得到远场假设条件下在M点散射中心的目标回波为
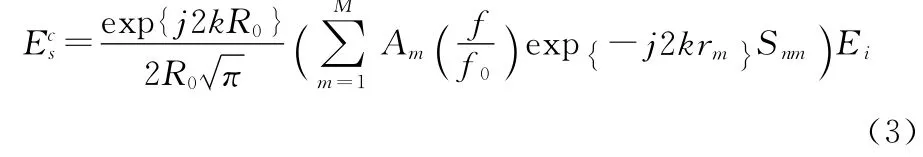
宽带极化散射矩阵为(忽略绝对强度):
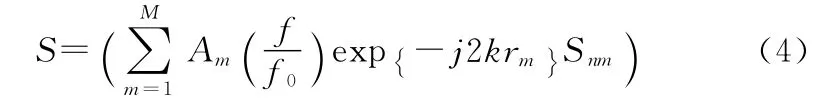
将式(4)展开得到两点散射中心宽带散射矩阵为

在远场条件下,(5)可以简化为

可见,复杂目标的散射矩阵不仅受入射频率的影响,同时受到散射中心类型、反射强度以及相对距离的影响,其中相对距离造成的相位影响对散射矩阵的影响是很明显的。
如果上面模型中的两个点散射中心中心散射性质是完全相同的,那么式(6)就可以简化为

散射中心的类型参数与散射中心的几何形状的关系如表1所示。

表1 散射中心的类型参数与散射中心的几何形状的关系
典型简单体目标在互易条件下的极化后向散射矩阵如表2所示。

表2 典型简单体目标在互易条件下的极化后向散射矩阵
可见,如果两个散射中心为点模型,那么散射中心的类型参数为0,那么式(7)可简化为


如果两个点散射中心模型的材质等不一样,则其散射强度也不一样,此时式(6)变为

此时散射矩阵受两点距离的影响就十分明显了。
如果它们是在空间具有不同的旋转角度ψ的线目标,那么由式(6)得
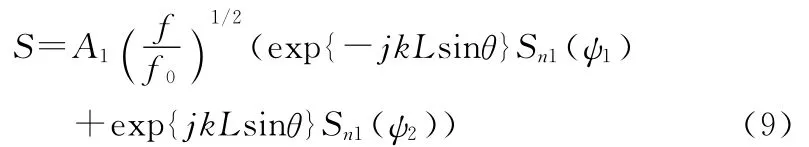
如果两个线散射中心的旋转角度完全一致的话,式(9)变为

由式(10)可知,完全相同的线散射中心的散射系数包络受频率调制,如图2所示。
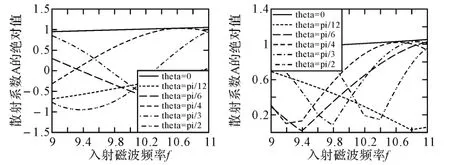
图2 完全相同的线散射中心的散射系数随入射波频率的变化(单位:GHz)
这里k为波数,两散射中心距离L=0.08 m,θ=0,π/6,π/12,π/4,π/3,π/2,A1=1/2。可见,散射系数的大小随入射频率的改变变化十分明显。
2.3 空间姿态变化的雷达目标的极化散射特性
按照在上一节讨论的点简单散射模型的情况下,由属性散射中心的定义,可以推导得出频域属性每个散射中心模型可以简化为

其中Am表征第m个散射中心相对散射幅度的复标量。xm,ym分别表示第m个散射中心在参考位置坐标系中的坐标。
同样,此频域表达式可以扩展到宽带极化散射矩阵的定义,那么

这里,Snm为第m个散射中心的归一化散射矩阵。
如果继续按照上面的点简单散射模型假设,那么式(12)变为

如果适合转台测量结果,不妨令两散射点的连线与雷达视线的夹角为θ,那么式(13)和式(7)是一致的。
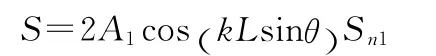
那么其归一化散射矩阵并不发生变化,其散射系数随方位角的变化如图3所示。
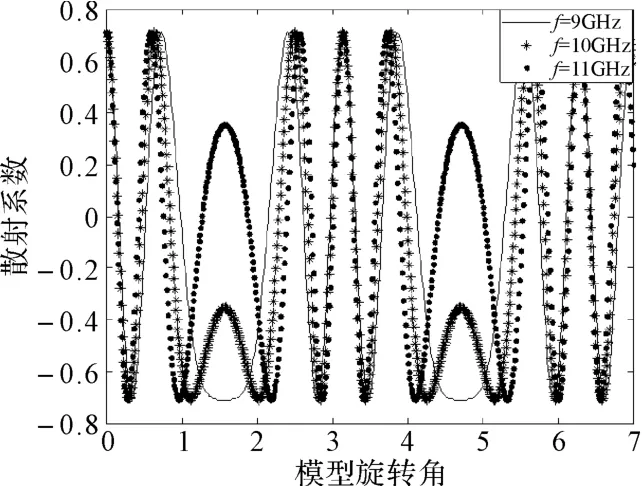
图3 不同频率下散射系数幅度随空间方位角的变化规律
可见,随着波长的减小,散射中心间距的模糊度越大,这主要是由于分辨单元跨越多个波长引起的。
3 基于矩量法的FEKO中的仿真与分析


图4 目标散射系数随空间姿态变化的仿真值
可见按照式(7)中的理论值与仿真值吻合得比较好,也验证了以上理论推导的正确性。
4 结语
本文从两点散射模型出发,利用几何绕射理论(GTD模型)建立了极化宽带散射模型,分析了模型的极化散射特性随入射电磁波频率与其空间姿态敏感变化的规律,并用矩量法进行了电磁计算仿真,验证了结论的正确性。这在雷达目标的距离像、目标重构、宽带极化测量等领域具有很大的应用潜力。对于其他雷达目标,都可以利用电磁矩量法等方法验证此理论推导的正确性。
[1]Wanielik G,Stock D J R.Broadband scattering matrix measurements and their modeling[M].IEEE Antennas and Propagation Society International Symposium,Ontario,1991.
[2]S W.MarCUS.Dynamics and radar cross section density of chaff clouds[J].IEEE Trans on AES,2004,40(1):93-102.
[3]汪茂光.几何绕射理论[M].第二版.西安:西安电子科技大学出版社,1985,6.
[4]刘涛.瞬态极化统计理论及应用研究[D].长沙:国防科学技术大学博士学位论文,2007,10.
[5]闫照文,苏东林,袁晓梅.FEKO5.4电磁场分析技术与实例详解[M].北京:中国水利水电出版社,2009:1-22.
[6]范丽思,崔耀中.FEKO实例教程[M].北京:国防工业出版社,2012,1:3-9.
[7]王雪松.宽带极化信息处理的研究[D].长沙:国防科技大学电子科学与工程学院博士学位论文,1999,6.
[8]陈静.雷达箔条干扰原理[M].北京:国防工业出版社,2007.
[9]李永祯,肖顺平,王雪松.雷达极化抗干扰技术[M].北京:国防工业出版社,2010,9:13-79.
[10]曾清平.雷达极化技术与极化信息应用[M].北京:国防工业出版社,2006.
[11]赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,2003.
