Lawrence-Gurney模型对于激光驱动飞片的适用性分析
2013-11-28牛锦超龚自正
牛锦超,龚自正 ,曹 燕
(1. 可靠性与环境工程技术重点实验室; 2. 北京卫星环境工程研究所:北京 100094)
0 引言
激光驱动飞片技术是一种新型动态高压加载技术,用于在超高应变率下材料动态响应、物态方程、炸药安全引爆以及空间碎片撞击等领域的研究,具有广阔的应用前景[1-6]。在激光驱动飞片的过程中涉及激光与材料的相互作用、材料物态的变化(熔融、气化、等离子体化等)、等离子体对激光的吸收和屏蔽作用、冲击波的相互作用等物理问题,针对这些问题要进行完整的理论描述和精确的数学求解非常困难。因此,人们在研究中提出一些假设或近似条件,忽略部分不重要的影响因素,建立较简单的物理解析模型,对飞片速度等物理量进行预估分析。
目前已建立的激光驱动飞片解析模型,大多数是在爆炸力学中的 Gurney模型的基础上发展而来,用于估算飞片能够获得的终极速度。1992年,美国Sandia国家实验室的Lawrence等[7]将Gurney模型应用到激光驱动飞片的理论研究之中,建立了描述激光驱动飞片过程的理论模型,即 Lawrence-Gurney模型。1997年,中国工程物理研究院的孙承纬等[8]在考虑相变状态方程的基础上,对 Gurney模型进行了改进。2005年,朱励等[9]结合变质量体系的动力学方程,提出了真空环境中强激光直接驱动飞片的计算模型。2007年,赵翔等[10]以激光支持的爆轰波(LSDW)理论为基础,建立了约束和无约束条件下激光驱动飞片的动量模型。在上述模型中,Lawrence-Gurney模型给出了主要试验参数与飞片速度之间的数学关系,便于应用。谷卓伟[11]和曹燕[12]等人均利用该模型进行了理论计算和分析。
随着激光驱动飞片试验技术的发展,特别是复合结构飞片靶的应用[13-16],激光和飞片之间的能量耦合效率显著提高,使得在试验中获得了较高的飞片速度。在新的试验技术条件下,本文拟从理论和试验两个方面对Lawrence-Gurney模型的适用性进行分析。
1 Lawrence-Gurney模型[7]
Lawrence将激光驱动飞片的过程简化为一维过程,不考虑激光与飞片相互作用的动态过程,整个驱动过程中飞片对激光能量的吸收率用有效吸收系数μeff表示,依据能量守恒和动量守恒定律建立数学方程组。Lawrence-Gurney模型给出了飞片参数(材料特性、厚度和直径等)和激光参数(能量、波长和脉宽等)与飞片速度之间的关系为

式中:μeff为有效吸收系数;ρ为飞片的材料密度;μa为飞片对激光的真实吸收系数;k为调节系数;α为热扩散系数;τ为激光脉宽;xd为激光对飞片的烧蚀深度;F0为激光能通量;r为激光能量损失率;εv为飞片材料的气化能;E为 Gurney能;v0为飞片的终极速度;x0为飞片的初始厚度(即产生飞片的金属膜层的厚度)。方程组的隐含求解条件为飞片的烧蚀深度远小于初始厚度,即xd<<x0。
参数r和k与飞片的材料特性无关,而与试验状态相关,需要一定数量的试验数据通过数学求解获得。
在Lawrence-Gurney模型中,能量耦合效率fE为飞片动能与激光能量的比值,冲量耦合系数 fM为飞片动量与激光能量的比值,在 xd<<x0的条件下,fE和fM分别为

2 理论计算与试验结果的对比分析
2.1 理论计算结果
针对波长1064 nm、脉宽(FWHM)15 ns的激光束的试验条件,假设聚焦光斑直径1 mm,激光能量密度0~400 J/cm2;铝飞片的初始厚度2~10 μm。利用Lawrence-Gurney模型进行理论计算所需的其他参数见表1[7],理论计算结果如图1所示。Lawrence在研究中利用25 μm厚的铝飞片对模型进行了试验验证[7],因此,本文特别针对25 μm厚铝飞片,给出了飞片速度、能量耦合效率fE、冲量耦合系数fM和飞片烧蚀深度随激光能量密度变化的计算结果。
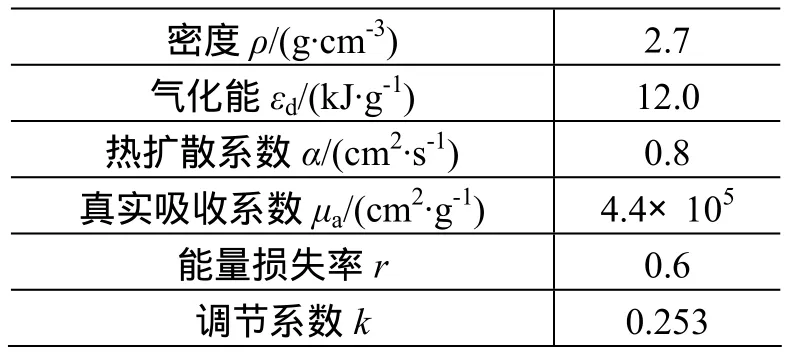
表1 铝飞片的材料特性参数Table 1 Material properties of aluminum flyer
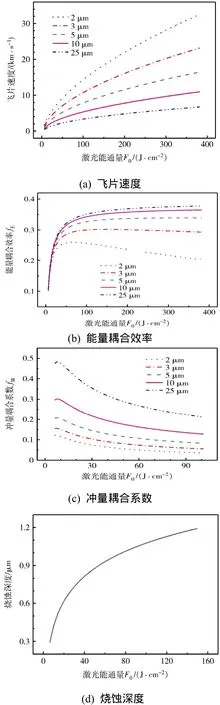
图1 Lawrence-Gurney模型的理论计算结果Fig. 1 Theoretical calculation results based on L-G model
从图1(a)可以看出,飞片速度随着激光能量密度的增大而加快,但增速逐渐变缓;在激光能量密度超过一定数值后,飞片速度呈近似线性增长,而且飞片越薄,线性关系的斜率越大。图1(b)表现出两种变化规律:当飞片厚度大于5 μm时,fE经历一个迅速上升的过程后趋于某一常数;而飞片厚度小于5 μm时,曲线则出现明显的拐点,在达到最大值后逐渐下降。fE始终小于0.4是因为在计算中假定r=0.6,即只有40%的激光能量可以转化为飞片的内能或动能。图1(c)说明冲量耦合系数曲线在激光能量密度较低时存在一个极大值点,且随着飞片厚度的增加,该点对应的激光能量密度稍有增加。图1(d)则反映出烧蚀深度与飞片厚度无关,而且在激光能量密度很低时xd就具有μm量级,因此飞片的初始厚度存在一个最小的阈值。
2.2 试验结果
利用波长1064 nm、脉宽15 ns的激光在0~2 J的能量范围内发射了不同厚度的铝飞片。飞片靶采用离子束溅射方法制备,其结构为石英玻璃/Cr膜/Al膜,其中Cr膜层厚50 nm,Al膜层厚3~10 μm;所发射飞片的直径为0.8~1.2 mm。试验结果如图2所示,其中,图 2(a)为飞片速度曲线,图 2(b)为能量耦合效率fE的曲线,图2(c)为冲量耦合系数fM的曲线。图2中, #1飞片靶(3 μm厚)不含有Cr层。为了便于分析,激光能量均换算为能量密度。
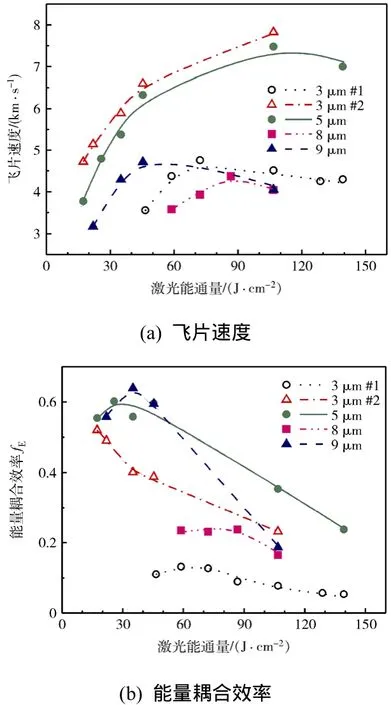

图2 激光驱动不同厚度铝飞片的试验结果Fig. 2 Experimental data for laser-driven aluminum flyers of different thicknesses
从图2中可以看出,对于厚度小于10 μm的飞片,其速度与激光能量间不具有单调变化关系:在激光能量较低时速度增加较快,随后变缓,当激光能量超过一定范围后飞片速度甚至开始下降。能量耦合效率随激光能量的增加而下降。冲量耦合系数曲线则呈现出单调下降趋势,在激光能量较低时近似线性地迅速降低,然后下降趋势变缓。
2.3 对比与分析
对比图1和图2,发现Lawrence-Gurney模型的试验结果与理论计算结果存在较大的差异:首先,试验中飞片速度的增加远低于理论计算的结果,而且出现了随激光能量增大而速度降低的情况。其次,能量耦合效率并未表现出随激光能量的增大逐渐增加并趋于某一常数的情形,而是主要表现为随激光能量的增大而降低,只在激光能量较低时曲线存在微弱上升趋势;但理论计算中当飞片厚度大于5 μm时,曲线不会出现下降趋势。最后,冲量耦合系数的试验曲线呈现单调递减的变化规律,不存在极大值点。
在上述差异中,冲量耦合系数曲线的差异可能是由于试验数据不足引起的。因为理论计算的结果显示曲线最大值对应的激光能量非常小,接近于能够发射飞片的临界激光能量,而试验中没有获得相应的数据。但是,飞片速度和能量耦合效率曲线并没有因为试验数据样本的缺陷而丢失重要信息。图2(b)所示的试验结果说明,在飞片厚度小于10 μm时,激光与飞片之间的能量耦合效率fE难以用某一常数进行衡量,这不满足Lawrence-Gurney模型的求解条件,造成方程组(1)无法求解。因此,Lawrence-Gurney模型不能真实描述厚度为10 μm以下飞片的驱动过程,无法准确预估飞片的终极速度。
造成理论计算结果和试验结果存在矛盾的可能原因还有很多,作者认为模型中关于烧蚀深度的假设和飞片加速过程的简化是两个重要的原因。首先,从图1(d)可以清晰看出,激光对飞片的烧蚀深度 xd随激光能量密度的增加而迅速增加,在激光能量密度为80 J/cm2时,xd约为1 μm,对5 μm厚的飞片意味着烧蚀比例高达20%;即使飞片厚度为10 μm,其烧蚀比例也达到10%。这不能很好地满足方程组(1)的数学求解条件 xd«x0,直接影响理论计算结果的有效性和准确性。其次,Lawrence-Gurney模型在简化时忽略了激光与飞片的相互作用过程,将飞片的动态加速过程简化为高压气体膨胀做功的过程,这种近似不适用于飞片较薄的情况。飞片较厚时,冲击波从激光辐照面到达自由面所需要的时间较长,飞片内部的波系相对简单,加速过程的简化不会带来显著的误差,因而能够较准确地计算飞片获得的终极速度。而飞片较薄时,冲击波很快就到达自由面并反射,飞片内形成复杂的波系,此时飞片受到的加速作用不能用简单的函数关系描述。因此,当飞片较薄时,理论计算的结果不能准确描述实际的情况。
由于目前无法通过理论计算或试验测量的方法获得飞片烧蚀深度的精确数据,而且图1(d)的数据是根据25 μm厚飞片的试验结果反推得到的,所以,对于厚度10 μm以下的飞片,xd与x0的关系有待进一步研究,这为Lawrence-Gurney模型的改进带来较大的困难。将Lawrence-Gurney模型中的激光能量损失率r视为动态变量[17],可以对模型进行简单的修正,但这种修正方法不能从本质上改变Lawrence-Gurney模型的缺陷,而且计算结果严重依赖试验数据,难以将结果外推到试验数据覆盖范围之外,因而适用性较差。
3 结束语
激光驱动飞片的物理过程非常复杂。Lawrence-Gurney模型利用一些等效性假设和数学近似,建立了求解飞片速度的数学方程组,能够在一定程度上反映主要试验参数与飞片速度之间的关系。但是,该模型不能较好地描述厚度 10 μm 以下飞片的驱动过程,主要原因是模型过于简单,简化忽略了激光与飞片的相互作用过程,忽略了飞片的动态加速特性。当飞片厚度小于10 μm时,如飞片的烧蚀深度应远小于初始厚度、能量耦合效率可用某一常数进行衡量等假设条件与方程组求解的数学条件都不能很好地成立。因此,有必要进一步对Lawrence-Gurney模型进行修正研究,以拓展其适用范围。
(References)
[1]Paisley D L, Warnes R H, Kopp R A. Laser-driven flat plate impacts to 100 GPa with sub-nanosecond pulse duration and resolution for material property studies [C]//Proceedings of APS, 1991: 825-828
[2]Tanaka K A, Motohiko H, Norimasa O, et al.Multi-layered flyer accelerated by laser induced shock waves[J]. Physics of Plasmas, 2000, 7(2): 676-680
[3]Trott W M, Setchell R E, Farnsworth A V Jr.Development of laser-driven flyer techniques for equation-of-state studies of microscale material[C]//Proceedings of AIP: CP620, 2002: 1347-1350
[4]Gu Z W, Sun C W. Experimental and numerical research on shock initiation of pentaerythritol tetranitrate by laser driven flyer plates[J]. Journal of Applied Physics, 2004,96(1): 344-347
[5]Robbins D L, Gehr R J, Harper R W, et al. Laser-driven miniflyer induced gold spall[C]//Proceedings of AIP:CP505, 2000: 1199-1202
[6]Roybal R, Tlomak P, Stein C, et al. Simulated space debris impact experiments on toughened laminated thin solar cell glass[J]. International Journal of Impact Engineering, 1999, 23: 811-821
[7]Lawrence R J, Trott W M. Theoretical analysis of a pulsed-laser-driven hypervelocity flyer launcher[J].International Journal of Impact Engineering, 1993, 14:439-449
[8]孙承纬, 庄仕明, 王春彦. 激光驱动飞片冲击引爆炸药的计算[J]. 强激光与粒子束, 1997, 9(3): 471-476 Sun Chengwei, Zhuang Shiming, Wang Chunyan.Calculation of impacting and detonating explosives by laser-driven flyers[J]. High Power Laser and Particle Beams, 1997, 9(3): 471-476
[9]朱励, 肖泰明, 郝军. 一个描述强激光驱动飞片高速运动的 Gurney模型[J]. 四川大学学报: 自然科学版,2005, 42(4): 775-778 Zhu Li, Xiao Taiming, Hao Jun. A Gurney model for the high velocity launch of laser-driven foil plate[J]. Journal of Sichuan University: Natural Science Edition, 2005,42(4): 775-778
[10]赵翔, 苏伟, 李东杰, 等. 激光驱动飞片的动量耦合模型研究[J]. 强激光与粒子束, 2007, 19(8): 1275-1278 Zhao Xiang, Su Wei, Li Dongjie, et al. Momentum coupling model for laser driven flying plates[J]. High Power Laser and Particle Beams, 2007, 19(8): 1275-1278
[11]谷卓伟. 激光驱动高速飞片的实验和理论研究[D].绵阳: 中国工程物理研究院博士学位论文, 2002
[12]曹燕. 激光驱动飞片超高速发射技术的理论和实验研究[D]. 北京: 中国空间技术研究院硕士学位论文, 2009
[13]Okada K, Wakabayashi K, Takenaka H, et al.Experimental technique for launching miniature flying plates using laser pulses[J]. International Journal of Impact Engineering, 2003, 29: 97-502
[14]Tadono T, Yoshida M, Takahashi E, et al. Flyer acceleration by a high-power KrF laser with a long pulse duration[J]. Journal of Applied Physics, 2000, 88(5):2943-2947
[15]Tanaka K, Motohiko H, Norimasa Ozaki, et al.Multi-layered flyer accelerated by laser induced shock waves[J]. Physics of Plasma, 2000, 7(2): 676-680
[16]Stahl D B, Gehr R J, Harper R W, et al. Flyer velocity characteristics of the laser-driven miniflyer system[C]//Proceedings of AIP: CP505, 2000: 1087-1090
[17]Bowden M D, Knowles S L. Optimization of laserdriven flyer velocity using photonic Doppler velocimetry[C]//Proceedings of SPIE, 2009, 7434
