基于正交HHT方法的一种高效地震波仿真研究

胡灿阳，陈清军，徐庆阳

（1.南京审计学院 江苏省公共工程审计重点实验室，南京 210029；2.同济大学 土木工程防灾国家重点实验室，上海 200092）

0 引言

地震动加速度［1］是联系地震和结构抗震的桥梁。在进行结构非线性分析和模型试验时都需要一组具有同一统计特性的地震动过程，然而地震的不确定性使我们无法得到满足这一要求的一组地震记录。所以根据特定目标谱来模拟地震动过程是地震工程中的一个重要研究方向。最常见的目标谱是符合某实际地震动记录的反应谱或功率谱。文献［2］以反应谱作为目标谱，通过反应谱和目标谱的转换关系来合成人工地震动。然而反应谱只能间接地反映地震动过程，无法准确地表现出地震动的时－频非平稳特性，它只适合于强度非平稳情况。为了能真实反映地震动的非平稳性质，用时变功率谱作为目标谱可以得到更加符合原地震记录时频特性的地震动样本，问题的关键是如何获得能够准确反映实际地震动时－频特性的时变谱。本文拟通过正交HHT 变换估计地震波的时变功率谱来进行非平稳地震地面运动模拟的研究。

1 基于正交HHT 变换估计地震动的时变功率谱

Huang等［3］提出了一种特别适合非平稳信号分析和处理的理论和方法，称为HHT。该方法是基于信号局部特征的，因此适用于非平稳信号的处理。相对于其它时频分解方法（如小波分析），HHT可以获得更为清晰的时频谱；相对于STFT 而言，HHT 可以获得更多频率信息，并有效表示出信号中的瞬态成分。但是Huang 等所提出的EMD 分解方法在理论上并不能保证严格的正交性，使得直接利用HHT 方法进行非平稳地震地面运动局部谱密度估计时，会存在能量泄漏，由它估计的局部谱密度不能作为原地震信号的时变谱密度。而通过正交HHT［4］变换估计地震动的时变功率谱可以使能量泄漏的问题得到很好的解决，可以作为时变功率谱的高效估计方法。

通过对EMD 分解得到的各阶IMF 分量进行正交化处理，得到了完全正交的各阶IMF 分量，其步骤如下：

（1）先将原信号进行EMD 分解，得到n个初始IMF分量c1′（t），c2′（t）…cn′（t）和残差rn（t）。把EMD分解得到的时程信号X（t）中除了残差的最后一阶IMF分量cn′（t），记作c1′（t）；即令c1（t）＝cn′（t），称为时程信号X（t）的第1阶正交化IMF分量；

（2）为了得到时程信号X（t）的第2 阶正交化IMF分量，应从cn－1′（t）中消除所含的c1（t）分量，即

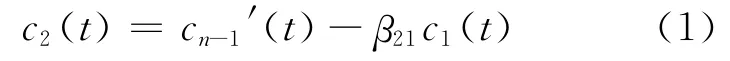
式中，β21称为cn－1′（t）与c1（t）之间的正交化系数，c2（t）称为时程信号X（t）的第2阶正交化IMF 分量。为了得到β21，可将式（1）的两边同乘c1（t）并对时间t进行积分，同时利用c2（t）与c1（t）的正交性，得到β21，并表示成离散形式，

（3）采用与上述相同的方法，从EMD 分解得到时程信号X（t）的第n－j阶初始IMF 分量中消除所含的从第1阶到第j阶正交化IMF 分量，则可得到时程信号X（t）的第j＋1 阶正交化IMF 分量cj＋1（t）（j＝1，…，n－1）。具体的正交化计算为：

为了得到βj＋1，i，将式（3）的两边同乘ck（t），（k≤j）并对时间t进行积分，利用ck（t）与ci（t），（i≠k）以及cj＋1（t）间的正交性，令i＝k时即可得到βj＋1，i，并将βj＋1，i表示成离散形式为，

经过上述步骤以后，X（t）被分解成了如下形式，

由此，分量cj（t）（j＝1，2，…，n）之间是完全正交的，通过线性变换得到的c＊j（t）（j＝1，2，…，n）之间也是完全正交的。这样，信号X（t）被分解成为n个正交的IMF 分量c＊j（t）（j＝1，2，…，n）及余量rn（t）的和。上述提取正交IMF分量过程并没有改变EMD 分解的原有过程，只是在提取了IMF 后对它们进行了正交化，即在数学意义上的重组。因此，这个正交化过程，能在严格保证IMF 属性的基础上，使之具有准确的正交性。

对于正交后的任一IMF 分量c＊（t）作Hilbert变换即得到（t）：

式中P代表柯西主值，则对于c＊（t）的解析信号z（t）为：

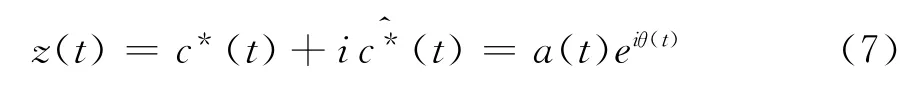
a（t）和θ（t）分别为信号的瞬时频率和瞬时相位。把信号振幅显示在频率－时间平面上，就可以得到Hilbert幅值谱H（ω，t），称为Hilbert谱，记作：

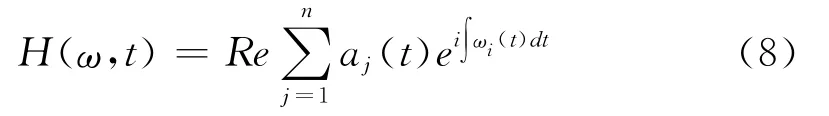
H（ω，t）精确地描述了信号的幅值随时间和频率的变化规律。由此可以得到原随机信号的局部功率谱密度［5］，即

由此可见，通过正交HHT 变换（OHHT）的时频特性，将随机过程或样本的能量进行了时频局部化，即其能量在时间和频率构成的平面上被展开，如（9）式，从而得到了随机过程或样本的时频局部特性——局部谱密度。信号通过正交HHT 变换后得到的Hilbert谱与局部谱密度的这种简单的关系，使利用正交HHT 变换进行局部谱密度的估计非常方便。

利用Husid［6］图可以定量的检验估计局部谱密度对地震波的时间局部特性反映的准确性。利用（9）式可得到地震波能量在时间上的分布，把每一时刻和此前所有时刻的能量累加可以得到地震波的Husid图。通过对比它和实际地震波的能量Husid图就可以定量的检验正交HHT 变换所估计的地震波局部谱密度对强度非平稳估计的准确性。图1为对三条著名地震波分别采用正交HHT 法和常规HHT 法所估计的地震波局部谱密度的能量归一化Husid图。

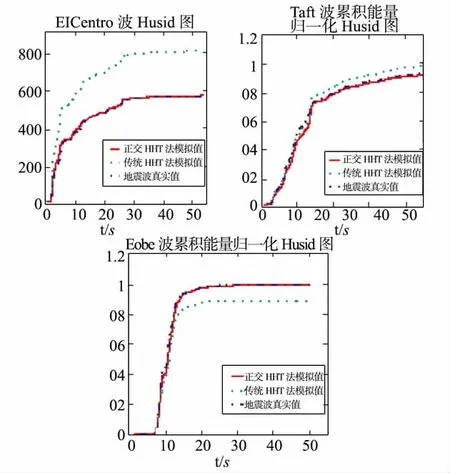
图1 OHHT和HHT估计的地震波能量归一化Husid图

地震波Husid图是能量随时间积累的曲线，反映了地震波强度随时间变化的局部特性。从图1可以看出，用正交HHT 法估计地震地面运动的局部谱密度得到的Husid图模拟值与地震波真实值吻合得很好，而且模拟值总能量和真实值一致，说明正交HHT 法在估计局部谱密度时没有能量泄漏，表明了它在反映地震波能量在时间上的分布方面有着很高的精度。而直接用HHT 法对这三条波估计时都有较大的能量泄露，EI Centro波的能量泄露高达30%。因此，在对原信号局部功率谱密度进行估计时，各IMF的正交性是必需的。

2 基于正交HHT 变换的非平稳地震地面运动模拟

Scanlan和Sachs［7］建议了利用三角级数法和演变谱模拟地震波的表达式：

为了模拟地震记录的时频非平稳特性，这里f（t，ωk）采用时变谱，Δω＝（ωk－ωk－1）为时变谱的频率间隔，Φk是［0，2π］区间均匀分布、相互独立的随机相位角。用普遍使用的多重过滤［8］或短时傅立叶变换（STFT）［9］估计地震波时变谱不仅速度慢、精度不高，而且如果在谱估计时为了提高精度，需要把Δω取得很小，导致在估计时变谱时非常费时，难以满足大量地震波模拟的需要。由图1可见，常规HHT 功率谱存在能量泄漏，无法作为目标谱来模拟地震波，本文使用正交HHT 功率谱作为时变谱进行地震波的模拟。利用正交化后HHT 变换可以快速、准确地估计出能够全面反映地震波时－频非平稳特性的时变谱，其精度和速度明显高于STFT和多重过滤，使得快速进行大量非平稳地震波模拟成为可能。

以El Centro地震波和1条Landers地震记录为目标进行模拟。图2为El Centro波地震记录和生成的3条样本。图3为Landers波地震记录及生成的3条样本。

由图2和图3可以看出，2 条波的样本曲线都能反映和原地震记录一样的强度随时间的变化趋势，特别是Landers波的2组加速度峰值的大小和分布都得到了很好的再现。这里每条样本的峰值和原记录不一定完全一致，但是可以从统计上来研究模拟波强度峰值的精度。为此，同时用多重过滤功率谱和STFT 功率谱作为目标谱来模拟地震波，同样各生成1000个样本。限于篇幅，这里不做出它们的样本曲线。图4和图5分别是用这3种目标功率谱生成1000个样本的标准差。

图2 El Centro波地震记录和生成的样本

图3 Landers波地震记录和生成的样本

图4 El Centro波1000个样本标准差

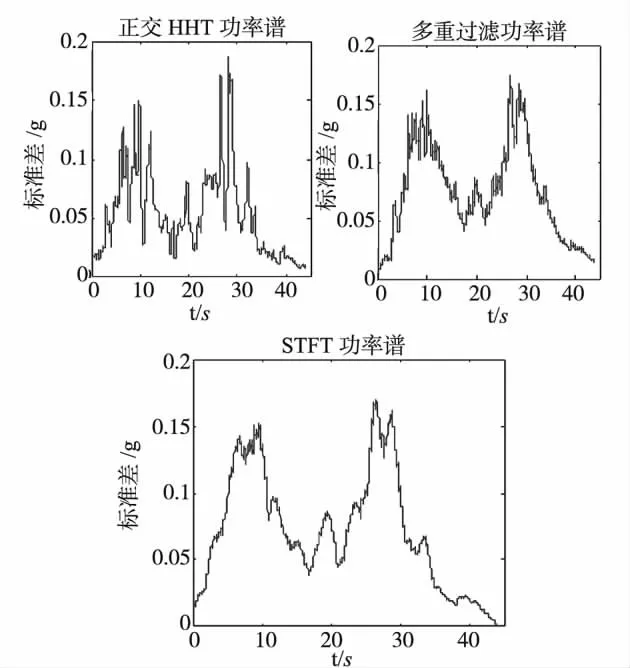
图5 Landers波1000个样本标准差

对于每个地震波，不同样本的峰值大小、峰值个数和峰值出现位置都不相同。以样本的加速度峰值大小为例：对于El Centro波，正交HHT 功率谱生成3个样本的最大峰值分别是相应标准差的2.09、1.63、1.46倍；对应于多重过滤功率谱，3个样本的最大峰值分别是相应标准差的2.20、3.00、2.69倍；对应于STFT 功率谱，3个样本的最大峰值分别是相应标准差的2.72、1.93、2.99 倍。对于Landers波，它有2组峰值。对应于正交HHT 功率谱，3个样本的第1 组峰值分别是相应标准差的2.38、2.14、1.83 倍；第2 组 峰 值 分 别 是 相 应 标 准 差 的2.17、1.84、1.82倍。对应于多重过滤功率谱，3个样本的第1 组峰值分别是相应标准差的3.55、2.12、2.52倍；第2 组 峰 值 分 别 是 相 应 标 准 差 的3.34、2.08、2.56倍。对应于STFT 功率谱，3个样本的第1组峰值分别是相应标准差的2.96、2.32、2.28 倍；第2 组峰值分别是相应标准差的2.56、2.09、2.67倍。从样本过程峰值大小的离散程度来看，模拟产生地震波的强度大小比较理想。

由上面可以看出，以正交HHT 功率谱作为目标谱并通过三角级数法生成的地震波能很好地反映原地震记录的强度非平稳特性。

此外，从图2和图3也可以直观地看出样本频率随时间的变化趋势和原记录相符合。图6和图7分别是2个波和任意一个模拟样本的傅立叶幅值谱。由图可见，样本和原记录的频谱特性比较接近。为了更好地检验强震记录和生成样本的时－频非平稳特性，图8和图9分别为2个波和它们的样本在时－频面上的Hilbert谱，由此可以看出能量在时－频面上的分布情况。从图上可以看出，样本的Hilbert时－频谱分布和原记录吻合的较好，样本能较准确地反映原强震记录的时－频非平稳特性。

图6 El Centro波和模拟样本的傅氏频谱

图7 Landers波和模拟样本的傅氏频谱

图8 El Centro波和模拟样本的Hilbert谱

图9 Landers波和模拟样本的Hilbert谱

3 结论

在总结常用非平稳地震时变功率谱估计的基础上，本文通过正交HHT 功率谱和三角级数法来模拟非平稳地震波。正交HHT 功率谱避免了常规HHT 功率谱的能量泄漏，在时间和频率上都能很好地反映原地震记录的非平稳特性，因此以它作为目标谱生成样本的强度和频率都是非平稳的。任意一个样本过程的时变谱不一定符合目标谱，但是在统计意义上严格符合。算例表明，本文的方法既能满足地震波非平稳的宏观特性，又在数值上具有很好的模拟精度，这样可以为某一强震记录补充大量具有相同统计特性的样本波，有利于结构随机响应时程分析。

正交化HHT 法可以有效地避免EMD 分解时的能量泄漏，但不能解决端点效应［10］等HHT 自身的缺陷，所以正交HHT 功率谱还有可能存在失真现象。如果能够解决端点效应问题，本方法将会很好地应用于地震波仿真和其它非平稳信号（如风波、水波、铁路和公路的振动信号等）的模拟，会具有广泛地应用前景。

［1］ 肖本夫，万永革，祁玉萍.强干扰环境下有效数字地震信号的提取［J］.华北地震科学，2011，（1）：6－9.

［2］ 蒋溥，戴丽思.工程地震学概论［M］.北京：地震出版社，1993：90－94.

［3］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454：903－995.

［4］ 楼梦麟，黄天立.正交化经验模式分解方法［J］.同济大学学报（自然科学版），2007，35（3）：293－298.

［5］ 胡灿阳，陈清军.基于HHT 法的地震地面运动局部谱密度估计［J］.振动与冲击，2007，26（10）：126－131.

［6］ Husid R L.Analisis de Terremotos：Analisis General［J］.Revista del ID1EM，1969，Santiago Chile，8（1）：21－42.

［7］ Shinozuka J，Jan C M.Simulation of random processes and its applications［J］.J.Sound and Vibration，1972，25（1）：111－128.

［8］ Priestly M B.Power spectral analysis of non－stationary random process［J］.J.Sound and Vibration，1967，6：86－97.

［9］ Mark W D.Spectral analysis of the convolution and filtering of non－stationary stochastic processes［J］.J.Sound and Vibration，1970，11：19－63.

［10］ 罗奇峰，石春香.Hilbert－Huang变换理论及其计算中的问题［J］.同济大学学报（自然科学版），2003，31（6）：637－640.