高强混凝土单轴动态抗压本构关系研究

曹立志，郭 赛

（河北省晋州市久洲建筑工程有限公司，河北 晋州 052260）

0 引言

混凝土的本构关系是进行混凝土结构计算的前提，只有使用准确合理的本构关系，才能对混凝土结构的受力做出准确的判断，做到结构合理受力，安全可靠。相比静态荷载的本构关系，混凝土在动态荷载作用下的本构关系就显得更为复杂了。混凝土材料从受力到破坏经历弹性阶段、非线弹性阶段和塑性阶段，材料的应力应变处于不同的阶段对应着不同的本构关系。构建混凝土本构关系时，一般是根据混凝土材料的力学及变形特性，通过试验确定本构关系中所需要的各种力学参数。由于非线弹性本构模型能够全面展示混凝土受力过程中非线性变形的主要特点，应力应变之间的关系公式及其参数是根据试验数据得到的，在单轴加载情况下，其计算结果是很有说服力的，因此得到了广泛的应用。文中将根据混凝土动态试验的结果来构建混凝土的动态非线性本构关系模型。

1 混凝土抗压本构关系概述

本构关系是描述混凝土力学与变形特性的重要方式，是建立多轴本构关系理论的基础。混凝土单轴抗压本构模型是《混凝土结构设计规范》引入的基础模型，可以通过进行系统的试验，得出混凝土的单轴抗压应力应变关系曲线，从而经过分析计算得出混凝土的单轴抗压本构模型。

许多研究人员为了能够更加准确的描述混凝土的抗压应力应变关系曲线，进行了大量的试验与理论研究，提出了多种形式的本构关系模型，如多项式、指数表达式、有理分式、三角函数表达式、统一方程和分段表达式等。不同表达式给出的混凝土本构关系计算模型如表1所示。

表1 混凝土本构关系表达式

本构关系模型如式（1）所示。

式中：αa为混凝土单轴抗压应力应变曲线的上升段参数；

αd为混凝土单轴抗压应力应变曲线的下降段参数；

f＊c为混凝土单轴抗压强度；

εc为与f＊c相对应的混凝土抗压峰值应变。

目前应用比较广泛的本构模型是Saenz模型，如式（2）、式（3）。

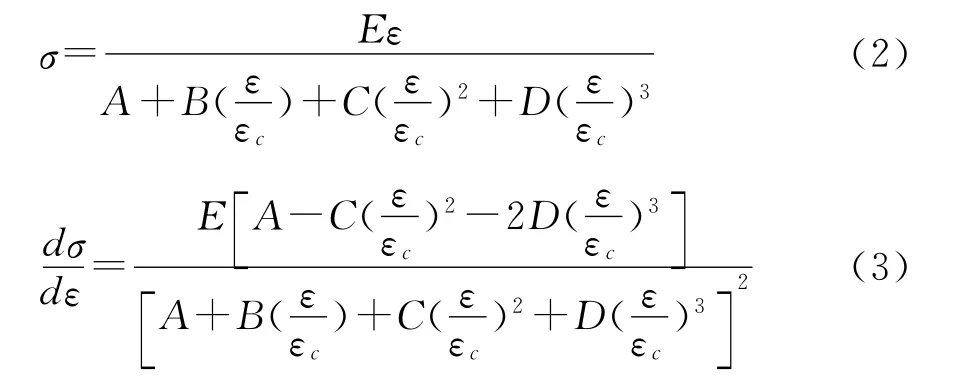
式中：E为弹性模量；A、B、C、D为计算常数，由下列条件求出。

（1）ε＝0，σ＝0；

（2）ε＝0，（应力应变曲线上原点处的切线模量）；

（3）ε＝εc，σ＝σ0（混凝土初始应力）；

（4）ε＝εc

取A＝1，C＝1，D＝0，就得到了在钢筋混凝土结构中应用广泛的Saenz简化模型，如式（4）所示。

式中：σs为峰值应力；

εc为混凝土的抗压峰值应变；

E0为混凝土的初始弹性模量；

ES为峰值应力处的割线模量。

Sargin（萨尔金）对Saenz公式进了修正，得到了如下模型：

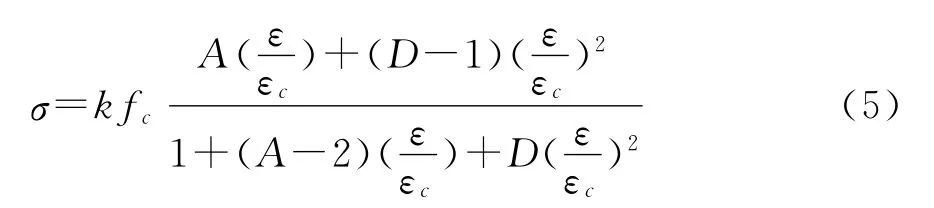
式中：A＝E0／Ec，E0为初始弹性模量，Ec为峰值应力处的割线模量；fc为混凝土立方体抗压强度；

k＝σ0／fc表示侧限对强度的影响系数，k＝1时，表示无侧向约束的素混凝土；

D是影响下降段的参数，0≤D≤1.0，D值越大，表示混凝土应力应变曲线下降段趋势越平缓，如图1所示。

图1 Sargin公式示意图

目前还没有通用的混凝土本构模型，只能结合工程的实际要求来选择合适的模型。本文结合试验结果，引入应变速率的影响参数，来构建高强混凝土本构关系模型。

2 高强混凝土单轴动态抗压本构关系的建立

试验表明，混凝土动态抗压强度及弹性模量均随应变速率的增加而增大，CEB（欧洲国际混凝土学会）建议的混凝土的抗压强度及弹性模量动态增加系数计算公式如式（6）～（8）和（9）所示。

式中：fsc为混凝土准静态抗压强度；

为实际应变速率；

为准静态和动态应变速率；

应变速率是指单位时间内应变的改变量，计算采用的本构模型不同，应变速率的计算公式及形式也不相同。本文拟构造非线弹性本构模型，则采用的应变率就是总应变率，即计算时间段内总的应变对时间的比值。

应变速率提高因子是对准静态力学性能的修正，本文用到的应变速率提高因子包括强度提高因子和模量提高因子。采用CEB 推荐的公式来计算强度的提高因子和弹性模量的提高因子，如式（11）和（12）。

动态荷载作用下的混凝土峰值应变没有明显的变化，而峰值应力却随应变速率的增加有明显的提高。因此构建混凝土动态本构模型时，峰值应变就取动态荷载下的峰值应变，对于动态峰值割线模量则引入应变速率来修正，即：

综上分析，得到考虑应变速率影响的混凝土抗压本构模型：

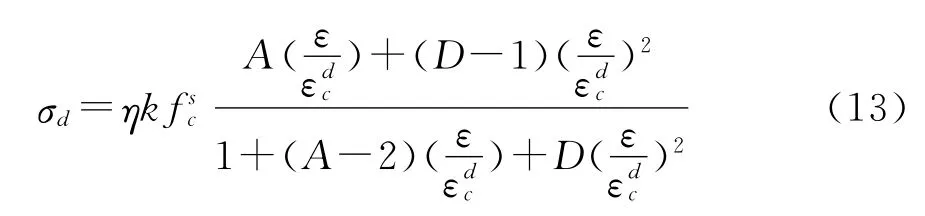
其中：A＝Ed0／Edc＝γE0／ηfsc／εdc；

ε、εdc分别为动态应变和动态峰值应变；

D根据试验应力应变曲线形状取0.5。

3 动态本构模型的验证

根据高强混凝土单轴动态抗压试验得到的数据对本构模型进行验证。视1×10－5／s为准静态应变速率，C60混凝土的准静态抗压强度与弹性模量分别为：fc＝56.60MPa，E0＝4.261×104MPa。拟合后的抗压强度提高因子和弹性模量提高因子分别为：

应用本模型计算得出的高强混凝土极限抗压强度和40%左右峰值应变处的应力，将计算结果与试验结果相比，如表2和表3所示。

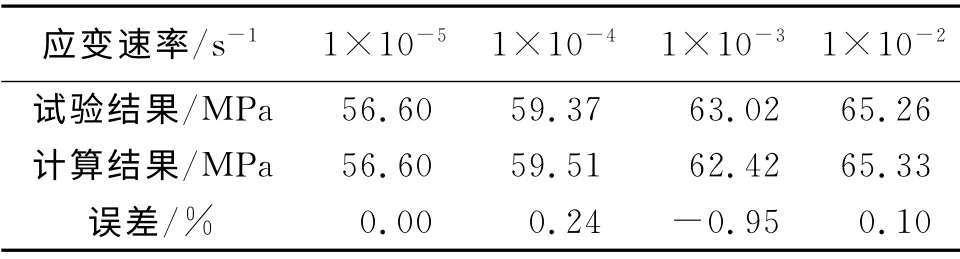
表2 C60混凝土峰值应力的模型计算值与试验值的比较

表3 C60混凝土40%左右峰值应变处的模型计算值与试验值的比较

从表2和表3中的数据可以看出，不同应变速率下的极限抗压强度模型计算结果与试验结果相差很小，而40%左右峰值应变处的应力模型计算结果与试验结果也相差不是很大，这说明建立的本构模型是正确的。

4 结论

在对Saenz提出的混凝土本构关系模型进行详细分析的基础上，通过引入的应变速率提高因子建立了混凝土单轴动态抗压本构关系模型，并通过混凝土单轴动态压缩试验数据对所建立的本构关系模型进行了验证，验证的结果表明：本文所建立的混凝土单轴动态抗压本构关系模型与试验数据之间能够很好的拟合，具有充分的说服力，是正确的。

［1］ 闫东明.混凝土动态力学性能试验与理论研究［D］.大连：大连理工大学，2006.

［2］ GB 50010－2010.混凝土结构设计规范［S］.北京：中国建筑工业出版社，2002.

［3］ Abrams D A.Effect of rate of application of load on the compressive strength of concrete［J］.Proc，20th Annu.Meeting，ASTM，West Conshohocken，Pa.1917，（17）：364－377.

［4］ Ross C A，Strain rate effects on dynamic fracture and strength［J］.ACI Materials Journal，1996，93（3）：293－300.

［5］ 尚仁杰.混凝土动态本构行为研究［D］.大连：大连理工大学，1994.

［6］ 孙吉书.混凝土单轴动态力学性能试验与本构关系的研究［D］.天津：河北工业大学，2012.