车下设备连接参数对车体振动特性影响研究
2013-11-27郭志成张立民
郝 刚,郭志成,张立民
(1 中国南车集团 青岛四方机车车辆股份有限公司,山东青岛266111;2 西南交通大学 牵引动力国家重点实验室,四川成都610031)
高速列车的电气、空调、制动控制等设备都直接或间接悬吊在车体底架上。设备自身或受到外界激励产生的振动直接通过底架传递给车体,引起车体局部振动,从而影响舒适度。激励也可能与车体局部结构或车下设备吊挂装置的固有频率相近,引起共振,从而使车辆局部或吊挂装置产生疲劳破坏。车下设备吊挂结构的振动特性直接关系到结构的可靠性,是列车安全运营需要考虑的重要因素之一[1]。我国的铁路列车以往运行速度不高,结构疲劳失效的问题不很突出,经过6次大提速,列车行车速度有了较大的提高,这样将使列车各部件承受的波动载荷加据,疲劳失效的问题逐渐暴露出来[2]。随着高速列车速度的不断提高,车体与车下设备之间的耦合振动更加复杂。车下设备吊挂装置的振动疲劳破坏已经成为某些车辆的重大问题。但是车体与车下设备耦合振动的激励来源、振动特性、减振设计方面并没有深入的研究。本文主要通过建立车下设备和车体的振动数学模型,并通过Matlab仿真研究设备吊挂安装结构参数对系统振动特性的影响。
1 模型建立
1.1 建立简化模型
根据自身有无振动源,车下设备可分为有源设备和无源设备。设备受到的激励来自有源设备的自身激励,或者外界的随机激励。一个系统的振动特性可以通过建立有限元模型或数学模型进行分析,本文通过建立简化数学模型进行振动分析,如图1所示。将车下设备简化为刚体,具有垂向位移z,车体简化为欧拉梁结构[3],横向位移为y(x,t)。文中重点研究车体静态时设备振动对车体振动的影响,忽略车辆一系、二系弹簧悬挂的影响。由于只考虑车体第一阶垂弯振动,欧拉梁简化为简支梁。长度为车辆的定长,不考虑设备重力引起的车体挠变形。设备与车体间的弹性元件简化为弹簧和阻尼,设备受到的外界激励为Q。

图1 计算模型
1.2 系统的振动微分方程
设备的振动微分方程为:
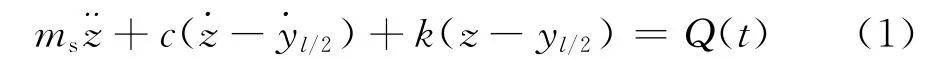
柔性梁的强迫振动微分方程:
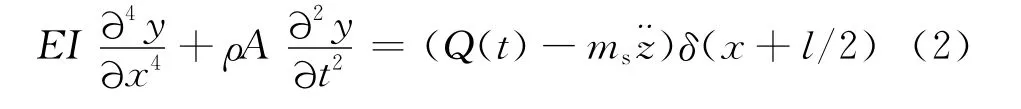
分离变量后,梁的微分方程解为:
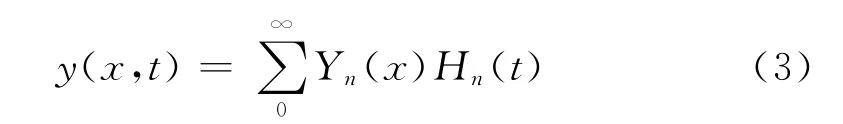
Yn(x)是梁固有频率pn下的正则振型函数;Hn(t)为未知的时间函数,即正则坐标。
根据主振型的正交性和δ函数的特性,式(2)两边同乘以振型函数Ym(x)dx,并且对x由0到l积分,可得车体各阶模态的强迫振动方程:

其中梁的各阶固有频率

考虑柔性梁的n阶振型,则可得到系统的n+1个微分方程。可将n+1个微分方程矩阵化[4-5]。文中只研究梁的第一阶模态,代入第一阶的振型函数。因此系统的振动微分方程为:
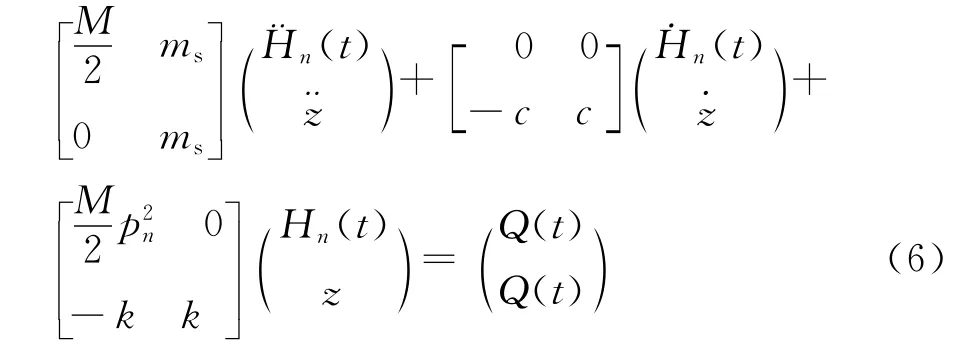
2 系统响应的频幅特性
以上建立的数学模型,虽经简化处理,但是仍然难以求得解析解,只能进行数值方法求解,本文使用Matlab编程,实现基于龙哥库塔法的系统运动方程的求解。采用某车辆参数(表1)求解其对于输入激励的幅频特性曲线。对于求解频幅特性曲线,输入的激励可以有多种方法,文中选择自动正弦慢扫描激励[6]。
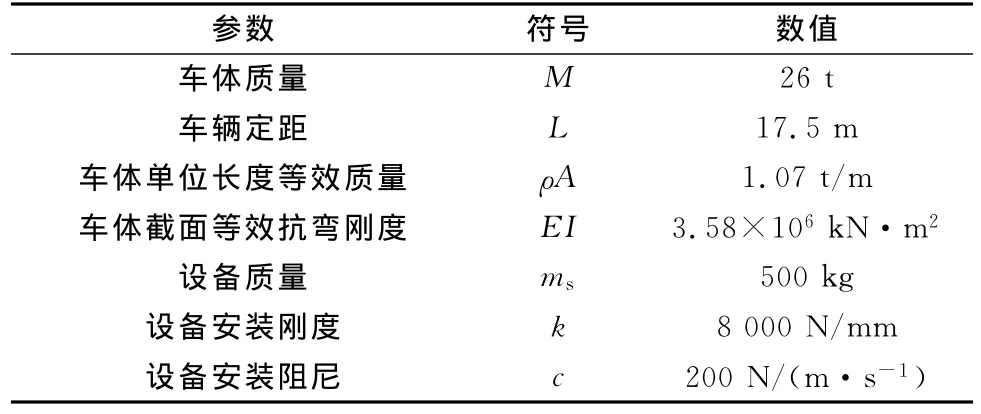
表1 某车辆参数
设备的激励Q(t)为0~50Hz的正弦扫频信号,计算得到车体中部响应yl/2和设备响应z的频响函数(图2、图3)。
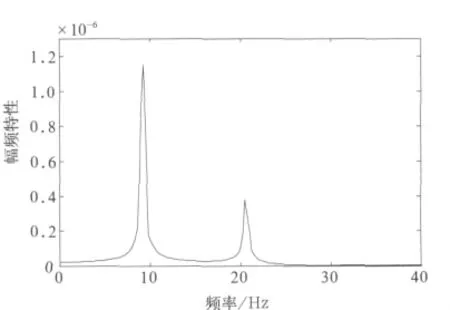
图2 车体中部响应的幅频特性
图3 设备响应的幅频特性
通过频响函数可以看出,车下设备和车体系统共有两阶模态:第一阶共振频率为9Hz,第二阶共振频率为21Hz。其中低阶为车体的垂弯模态,高阶主要为设备振动模态。在车体结构设计中,应尽量避免外界激励主频与车体—设备系统固有频率相同。对于有源设备的激励来说,可以通过振动设计避开设备激励的影响。但是对于来自轨道等随机激励,以及对于连续自由度车体来说,共振频率不可避免,这时可以通过设备结构参数来使振动最小。下面研究设备结构参数对系统振动特性的影响。
3 设备结构参数对系统振动特性的影响
对车体设备系统振动特性研究目的是为了减振设计,使设备的结构参数与车体的结构参数相匹配。以下分别讨论不同的设备质量(表2)、不同的安装刚度(表3)、不同的安装阻尼(表4)对系统振动特性的影响。

表2 设备的不同质量值 kg

表3 设备不同吊挂刚度值 N/mm

表4 设备不同吊挂阻尼值 N/(m·s-1)
3.1 设备质量对系统振动特性的影响

图4 不同设备质量下系统共振峰值响应
3.2 设备吊挂刚度对系统振动特性的影响
调整设备吊挂刚度k(表3),保持其他参数条件不变,计算车体中部响应yl/2和设备响应z在共振时的峰值响应(图5)。在刚度变化的整个区间上,随k值的增大,车体、设备的响应均减小。此种情况下,激励由设备上输入,不考虑车体激励(即静态)情况下,增大刚度可以明显抑制设备和车体振动。并且随k值的增大,二阶共振频率逐渐远离一阶共振频率。
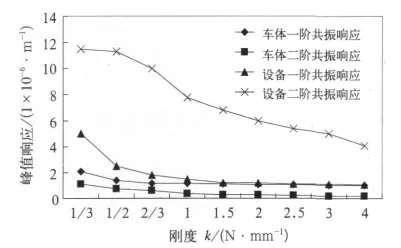
图5 不同吊挂刚度下系统共振峰值响应
3.3 设备吊挂阻尼对系统振动特性的影响
调整设备吊挂阻尼c(表4),保持其他参数条件不变,计算车体中部响应yl/2和设备响应z在共振时的峰值响应(图6)。在整个阻尼区间上,随着设备安装阻尼的增大,设备振动显著减小,车体的二阶振动响应也有所减小。车体和设备的一阶共振响应减小不明显,对阻尼变化并不明显。
3.4 设备吊挂刚度对系统振动影响试验验证
为验证设备吊挂刚度对车辆—设备系统振动的影响,通过试验研究了某动车车体与车下吊挂的变压器间连接刚度对系统振动的影响。连接刚度参数如表5。
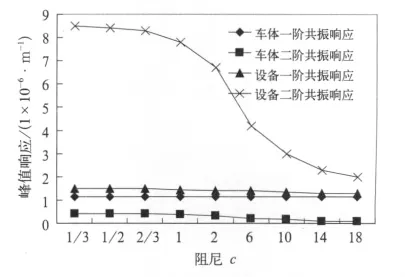
图6 不同吊挂阻尼下系统共振峰值响应

表5 试验选取的连接刚度值 N·mm-1
图7为车体和变压器共振响应峰值随设备安装刚度变化情况。在刚度变化的区间内,随k值的增大,车体、设备的响应均减小。由此可见,在连接静刚度不变的情况下,车体—设备振动特性随动刚度演变趋势与计算结果相同,验证了3.2节的计算结果。在实际验证性试验设备质量和连接阻尼参数调整较难实现,因此,本文在试验中未进行阻尼等参数的验证[7]。
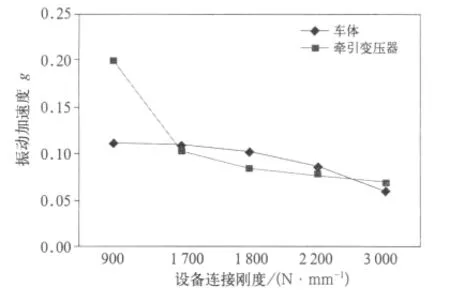
图7 不同吊挂刚度下系统共振峰值响应
4 结 论
(1)建立了车下设备 车体振动系统的简化模型,并对模型幅频特性进行研究;针对设备的不同结构参数,计算得出了不同结构参数对系统共振峰值的影响曲线。
(2)通过不同结构参数对峰值影响曲线分析,发现设备振动对结构参数的变化敏感,车体振动对结构参数的变化不敏感。在只考虑设备激励情况下,减小车体一阶共振响应可以采取的措施是减小设备质量,增大吊挂的刚度;减小设备二阶共振响应可以采取的措施是增大设备质量,增大吊挂刚度和阻尼。
(3)理论分析和试验验证结果都表明,随着设备质量和吊挂刚度的变化,系统的二阶频率会发生明显变化,这对调整系统固有频率、避免共振提供了有效手段。
[1]肖守讷.高速列车关键部件频域疲劳可靠性理论研究[J].学术动态,2009,(1):20-24.
[2]徐凤妹,劳世定.客车车下设备吊挂方式的研究[J].铁道车辆,2009,47(4):12-14.
[3]高淑英,沈火明.线性振动教材[M].北京:中国铁道出版社.2003.
[4]肖新标,沈火明.移动载荷作用下的桥梁振动及其TMD控制[J].振动与冲击,2005,24(2):58-61.
[5]许磊平,刘伟庆,徐秀丽.TMD抑制桥梁振动仿真分析[J].防灾减灾工程学报,2009,47(4):12-14.
[6]李德葆,陆秋海.实验模态分析及其应用[M].北京:科学出版社.2001,125-129.
[7]陈 亮,康洪军,张立民.牵引变压器连接刚度对车体与设备振动影响分析[J].铁道车辆,2012,50(8):4-6.
