混合分布在非一致性洪水频率分析的应用
2013-11-27冯平,曾杭,李新
冯 平,曾 杭,李 新
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
近年来,受气候变化尤其是人类活动的影响,许多流域内的下垫面条件发生了显著变化.下垫面变化的发生,会改变流域原有降雨产汇流过程,水文序列会发生显著变化,导致水文序列不满足一致性要求,则采用传统频率计算方法得到的结果将会受到质疑[1].基于非平稳极值系列的直接水文频率分析方法有3种:①基于混合分布的非一致性水文频率分析方法;②基于时变矩的非一致性水文频率分析方法[2];③基于条件概率分布的非一致性水文频率分析方法[3].笔者采用混合分布模型对非一致性水文频率分析进行探讨.Singh等[4]首次提出将混合分布模型应用到非一致性洪水频率计算,得到较好的效果,但参数估计是当时存在的最大问题;2002 年,Alila等[5]应用此方法对 Gila流域进行了研究,发现混合分布模型比传统的单分布模型更好.对于混合分布的参数估计问题,目前国内外学者采用了很多方法,如Singh[6]采用非线性优化算法、Rossi等[7]采用极大似然算法、Leytham[8]采用极大似然的 EM 算法以及Fiorentino等[9]采用最大熵准则法(POME).非线性优化算法是利用样本系列的前五阶中心距求解参数,对于小样本而言高阶矩会产生较大误差,后3种估计方法计算过程较为复杂.成静清等[10]采用模拟退火算法进行混合分布模型参数估计,应用于非一致性年径流序列的频率计算,取得较好效果;谢平等[11]对非一致性年径流序列的频率计算也取得了一些研究进展.然而非一致性洪水序列频率计算在我国缺乏系统成熟的方法,为此,笔者根据水文变异点的综合诊断结果,假设非一致性洪水序列变异点前后分别服从2个皮尔逊Ⅲ型分布,全序列服从由这2个分布组成的混合分布,以大清河流域南支上游龙门水库的入库年最大流量序列和固定时段(1日、3日、6日)洪量序列为例,分析变异后计算得到的设计洪水值与不考虑变异情况下的设计洪水值、原设计洪水值(1985年审定通过)之间的变化及变化原因,以期为龙门水库的设计洪水修订提供依据,也为大清河流域南支上游其他大型水库的设计洪水修订提供技术方法.
1 非一致性洪水序列变异点的诊断方法
水文时间序列变异点综合诊断方法首先是对洪水序列进行初步诊断,以检验序列是否存在确定性成分[12],即采用过程线法、累积曲线斜率差异幅度分析法和Hurst系数法进行初步检验.判断序列是否存在变异,若判断结果不存在变异,则转入成因调查分析,对结果进行确认;如存在变异,转入详细诊断部分.详细诊断主要采用 Lee-Heghinian检验、有序聚类检验、最优信息二分割检验、R/S检验和滑动 F检验等方法.最后进行综合诊断,结合详细诊断的可能变异点和物理成因分析,确定最可能变异点.
2 非一致性洪水序列的混合分布与参数估计
2.1 混合分布模型
早在 1972年 Singh等[4]首次提出将混合分布模型应用到非一致性洪水频率计算中,得到较好的效果.混合分布是由k个一致性的分布(子分布)混合而成的,即

式中:Fk( x)为k个子分布的累积分布函数;αk为各个分布的权重,且满足α1+α2+ …+αk=1.0.
根据 SL44—2006《水利水电工程设计洪水计算规范》规定,我国水文频率计算一般采用 P-Ⅲ型分布,故混合分布模型中的子分布可假设服从 P-Ⅲ型分布.为降低参数估计的复杂性,一般令一个混合分布由 2个子分布组成[5].因此,对于样本容量为n的非一致性水文时间序列X,若其变异点为τ,假设变异点之前的序列为X1,服从概率密度函数为f1( x)的分布,其样本长度为n1=τ;变异点之后的序列为X2,服从概率密度函数为 f2(x)的分布,其样本长度为整体序列X服从混合分布f( x),概率密度函数为
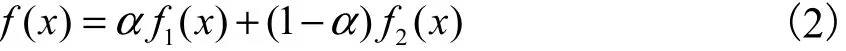
式中α为权重系数.
子分布的概率密度函数 f1( x)和 f2(x)均服从 P-Ⅲ型分布,其表达式为
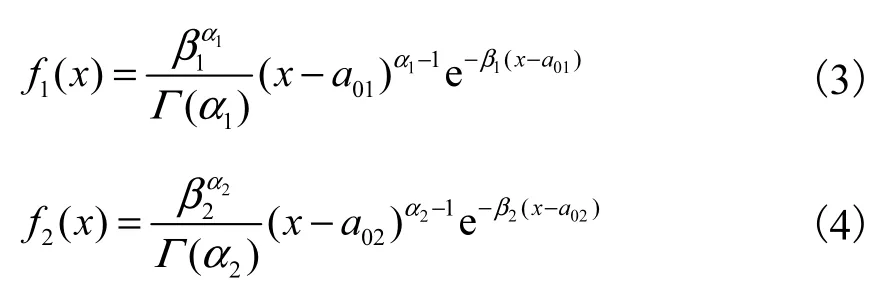
式中:αi、βi和a0i分别为fi( x)函数分布的形状、尺度和位置参数(i=1,2),可以由统计参数均值、变差系数Cvi和偏态系数Csi来表示,具体关系为因此,混合分布f( x)中有和Cs27个需要估计的参数.
2.2 参数估计
成静清等[10]在非一致性年径流序列频率参数计算中,将混合分布的参数估计问题看成是组合优化问题,采用全局优化算法——模拟退火算法[13]进行参数估计.模拟退火算法描述简单、使用灵活、运行效率高且受初始条件限制较少,本研究也选用此方法进行洪水序列频率分布参数估计的计算.
3 实例分析
大清河流域南支上游龙门水库位于河北省保定市满城县境内的漕河干流上,控制流域面积470,km2,总库容 1.27×108,m2,是一座以防洪为主结合灌溉等综合利用的大(Ⅱ)水利枢纽工程.水库始建于 1958年,1959—1960年扩建为大型水库,1974—1977年进行水库加固扩建工程,2002年开始实施水库除险加固工程,2006年水库防洪标准达到100年设计,2000年校核.
龙门水库的洪水资料有洪峰流量(1956—2005年)、年最大 1日洪量(1951—2005年)、年最大 3日洪量(1951—2005年)和年最大 6日洪量(1951—2005年)4个序列.
3.1 洪水序列变异点的诊断
3.1.1 初步诊断
分别采用累积曲线斜率差异幅度分析法和 Hurst系数法对龙门水库的 4个洪水序列进行诊断.累积曲线斜率差异幅度分析法,最大差异幅度大于 50%,判断为变异,反之无变异;Hurst系数法,Hurst系数值对应变异程度分级表,判断变异程度;2种方法均变异者即判断为变异序列.由表 1可知,1日洪量、3日洪量和6日洪量序列存在水文变异,洪峰流量序列不存在水文变异.

表1 龙门水库洪水序列水文变异初步诊断结果Tab.1 Initial diagnosis results of hydrological alteration of Longmen reservoir flood series
3.1.2 详细诊断
由初步诊断结果,采用 Lee-Heghinian检验、有序聚类检验、最优信息二分割检验、R/S检验和滑动F检验等方法,进行变异点的详细诊断,结果见表2.
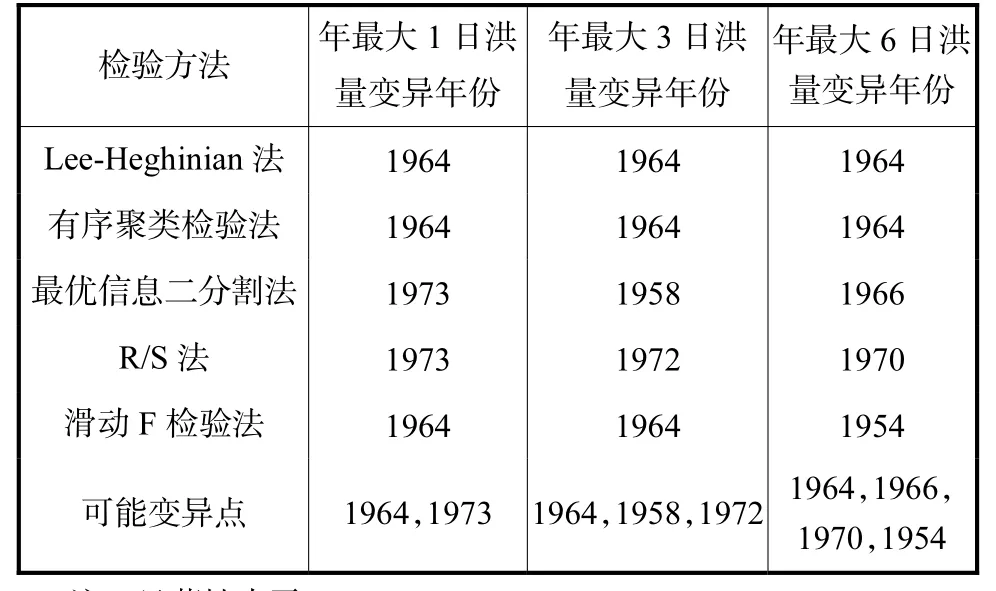
表2 不同方法下洪水序列水文变异详细诊断Tab.2 Detailed diagnosis of hydrological alteration of flood series by different methods年
3.1.3 综合诊断
综合诊断主要是在详细诊断可能变异点的基础上,结合流域水文自然地理环境和人类活动变化影响,进行成因分析.
由表2可知,龙门水库年最大1日洪量序列可能变异点为1964年和1973年,年最大3日洪量序列的可能变异点为1964年、1958年和1972年,年最大6日洪量序列的可能变异点有 1964年、1966年、1970年和1954年.龙门水库始建于1958年,其固定时段年最大洪量实测水文序列为 1951—2005年,可能变异点1958年和1954年位于水文序列首端,变异点不可靠;龙门水库于 1963年遭遇了建库以来最大的一次洪水,称“63.8”洪水,此场洪水是汛期特大暴雨导致的特大洪水,可能由气候变化引起,而由于气候变化原因复杂,需要长系列水文气象数据加以分析确认,因此从下垫面变化导致洪水变异的角度来说,1964年和 1966年变异点不作为最可能变异点;1974—1977年龙门水库进行加固扩建工程,且于 20世纪60年代末至70年代,大清河流域对上游大中型水库(包括龙门水库)进行了续建、扩建,基本形成以水库、蓄滞洪区、骨干河道为主的防洪工程体系,流域下垫面条件的改变十分显著,故诊断出的可能变异点1970年、1972年和1973年是合理可靠的.综上物理成因分析,龙门水库年最大 1日、3日和 6日洪量序列的变异点分别为1973年、1972年和1970年.
3.2 设计洪水成果比较分析
3.2.1 理论频率计算
1)曲线参数估计
对变异水文序列,由序列的变异点,以频率离差绝对值和最小准则(ABS)为目标函数,采用模拟退火算法对 2个 P-Ⅲ型混合分布的参数进行估计,结果详见表3.
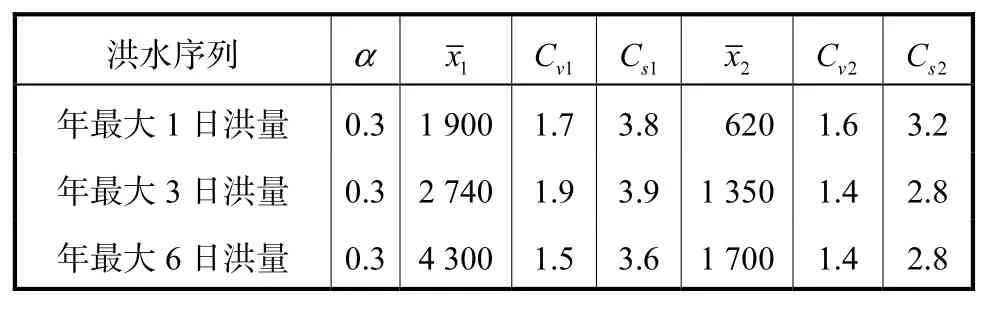
表3 变异序列的参数估计Tab.3 Parameter estimation of non-stationary series
2)理论频率计算
将计算得到的混合分布参数代入式(2)可得整个序列的理论频率,其计算函数为

3.2.2 频率曲线拟合
根据经验频率和理论频率,运用 K-S检验法进行拟合检验.在 K-S检验法中表示随机样本的累积频率函数,本文中为变异序列的经验频率.表 4给出了水文序列理论分布频率与经验分布频率的 KS检验.
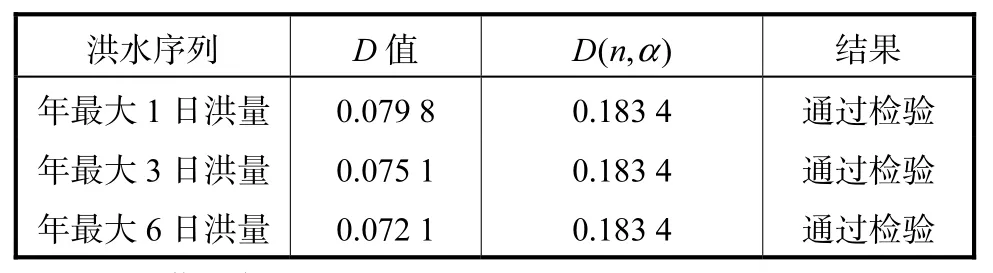
表4 龙门水库3个非一致水文序列K-S检验结果Tab.4 K-S test results of three non-stationary hydrological series of Longmen reservoir
从表4可知,不同固定时段年最大洪量的3个水文变异序列均通过显著性水平为 0.05的 K-S检验,说明样本序列服从混合分布.
不同时段(1日、3日和6日)年最大洪量水文序列的变异情况理论分布频率与经验分布频率拟合曲线和不考虑变异情况的 P-Ⅲ型分布频率曲线详见图1~图3.图1~图3分别为年最大1日洪量、年最大3日洪量和年最大 6日洪量序列的频率曲线.由图1~图 3可见,在离差绝对值和最小准则的情况下,相比不考虑变异情况下的传统 P-Ⅲ型分布频率曲线,3组变异序列混合分布曲线与经验点据拟合明显较好,尤其是经验点距频率较大部分.这说明2个P-Ⅲ型分布混合模型应用于非一致性洪水序列是可靠的,特别是存在水文序列变异的情况下,可以与经验点据整体拟合更好.

图1 龙门水库年最大1日洪量序列的频率曲线Fig.1 Frequency curves of annual maximum 1-day flood volume series of Longmen reservoir

图2 龙门水库年最大3日洪量序列的频率曲线Fig.2 Frequency curves of annual maximum 3-day flood volume series of Longmen reservoir
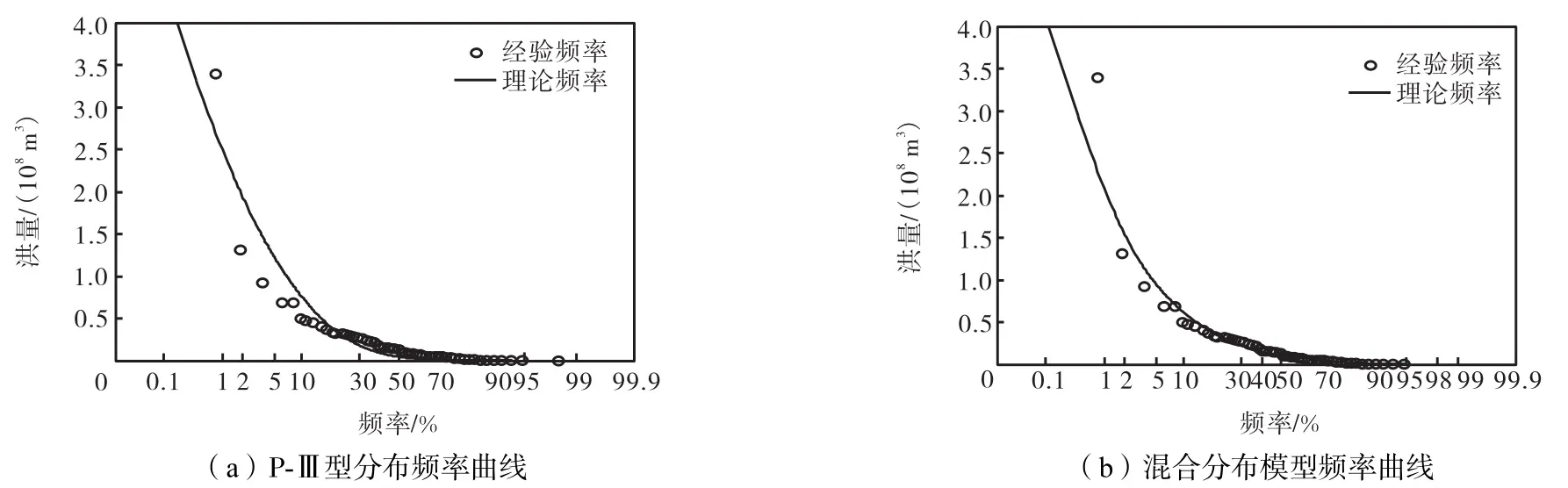
图3 龙门水库年最大6日洪量序列的频率曲线Fig.3 Frequency curves of annual maximum 6-day flood volume series of Longmen reservoir
3.2.3 设计洪水成果比较分析
对于考虑变异情况下龙门水库设计洪水的合理性,将通过与 1985年水利部规划总院审定的龙门水库设计洪水值,及不考虑变异情况下的 P-Ⅲ型分布给出的设计洪水值进行对比分析.表 5为龙门水库相应的不同设计洪水值及变化情况下的对比.
由表 5可见,诊断无变异的洪峰流量序列(1956—2005年),考虑历史特大洪水情况下,通过P-Ⅲ型分布频率适线,得到的不同标准设计洪水值相较1985年审定的设计洪水值均小,变小的比例在7.7%~30.0%;而固定时段(1日、3日和6日)年最大洪量序列均诊断出变异,且3个变异序列的变异点均在1970年附近,运用混合分布模型计算出不同设计标准的设计洪水值相比不考虑变异情况下的设计洪水值和 1985年审定的设计洪水值,也均有不同程度的减小,相较不考虑变异情况下的设计洪水值,年最大1日洪量值变化比例范围为 1.0%~20.8%;年最大 3日洪量变化比例范围在1.2%~23.7%;年最大6日洪量变化比例范围在 1.8%~22.1%,变异的程度均比较明显.从统计角度分析,现状洪水序列情况下得到的设计洪峰值和设计洪量值较1985年审定的设计洪峰值和设计洪量值小,前者可能由于样本长度增长所致,1985年审定的设计值需完善修订;得到的非一致性序列设计洪量值较不考虑变异情况的设计洪量值小,表明流域受下垫面变化和人类活动(水保措施和水利工程的兴建等)的影响,导致入库洪水减少的现象比较明显.这在一定程度上说明,在下垫面变化和人类活动影响比较大的大清河流域,进行设计洪水的校核与修订是非常必要的.
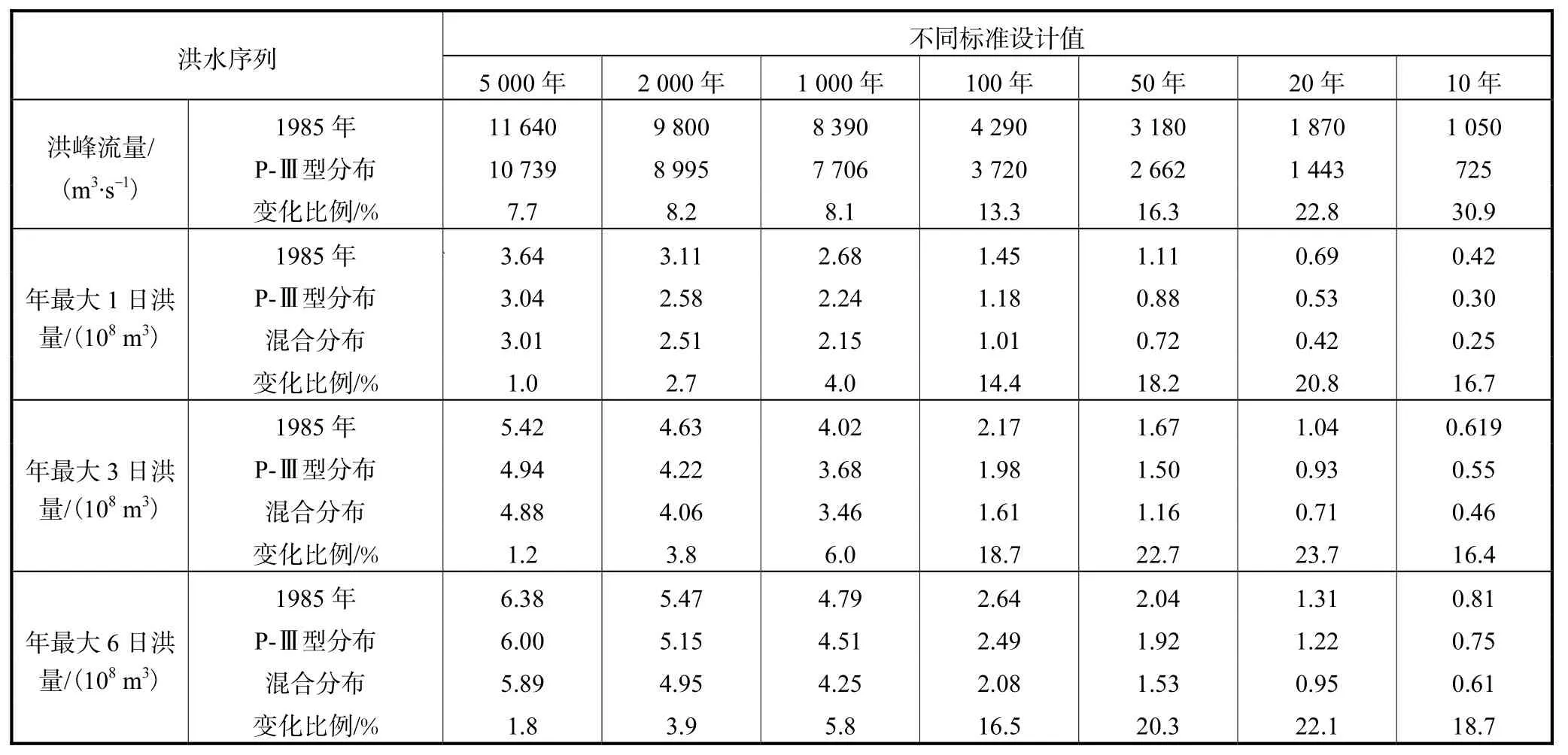
表5 龙门水库设计洪水成果比较Tab.5 Comparison of design flood values of Longmen reservoir
4 结 论
以大清河流域南支上游龙门水库为对象,着重研究了混合分布模型解决非一致性洪水序列频率计算的问题,并进一步分析非一致性水文序列后的设计洪水值与未变异前的设计洪水值之间的变化,得出以下主要结论:
(1) 采用变异点综合诊断方法和物理成因分析,可以较准确地判断洪水序列是否变异以及得到变异序列的变异点,诊断龙门水库固定时段(1日、3日、6日)年最大洪量序列存在变异,且 3个序列变异点年份相近.
(2) 采用模拟退火算法,以离差绝对值和最小准则为目标函数,可以比较可靠地进行参数估计,避免了人工适线的误差,实例证明得到的混合分布曲线与经验点据拟合较好,比较适合存在变异情况下的水文序列频率分析.
(3) 基于混合分布的非一致性洪水频率分析计算,不需要进行洪水资料的还原,完全从统计角度完成洪水频率分析计算,理论基础比较明确.
(4) 对于龙门水库的非一致性洪水序列,与不考虑变异情况的设计洪水值相比,不同设计标准的设计洪水值相比不考虑变异情况下的设计洪水值,也均有不同程度的减小,变化比例范围均在 1%~25%,变异的程度比较明显.因此,在下垫面变化和人类活动影响比较大的大清河流域,进行设计洪水的校核与修订是非常必要的.
[1] 梁忠民,胡义明,王 军. 非一致性水文频率分析的研究进展[J]. 水科学进展,2011,22(6):864-871.Liang Zhongmin,Hu Yiming,Wang Jun. Advances in hydrological frequency analysis of non-stationary time series[J].Advances in Water Science,2011,22(6):864-871(in Chinese).
[2] Strupczewski W G,Singh V P,Feluch W. Nonstationary approach to at-site flood frequency modeling(I):Maximum likelihood estimation[J].Journal of Hydrology,2001,248(1/2/3/4):123-142.
[3] 宋松柏,李 扬,蔡明科. 具有跳跃变异的非一致分布水文序列频率计算方法[J]. 水利学报,2012,43(6):734-739,748.Song Songbai,Li Yang,Cai Mingke. Methods of frequency analysis for hydrologic data with jump up components[J].Journal of Hydraulic Engineering,2012,43(6):734-739,748(in Chinese).
[4] Singh K P,Sinclair R A. Two-distribution method for flood frequency analysis[J].Journal of Hydraulics Division,1972,98(1):29-44.
[5] Alila Y,Mtiraoui A. Implications of heterogeneous flood-frequency distributions on traditional streamdischarge prediction techniques[J].Hydrological Processes,2002,16(5):1065-1084.
[6] Singh K P. A versatile flood frequency methodology[J].Water International,1987,12(3):139-145.
[7] Rossi F,Fiorentino M,Versace P. Two-component extreme value distribution for flood frequency analysis[J].Water Resources Research,1984,20(7):847-856.
[8] Leytham K M. Maximum likelihood estimates for the parameters of mixed distributions[J].Water Resources Research,1984,20(7):896-902.
[9] Fiorentino M,Arora K,Singh V P. The twocomponent extreme value distribution for flood frequency analysis:Derivation of a new estimation method[J].Stochastic Hydrology and Hydraulics,1987(1):199-208.
[10] 成静清,宋松柏. 基于混合分布非一致性年径流序列频率参数的计算[J]. 西北农林科技大学学报:自然科学版,2010,38(2):229-234.Cheng Jingqing,Song Songbai. Calculation of hydrological frequency parameters of inconsistent annual runoff series based on mixed distribution[J].Journal of Northwest A&F University:Natural Science Edition,2010,38(2):229-234(in Chinese).
[11] 谢 平,陈广才,夏 军. 变化环境下非一致性年径流序列的水文频率计算原理[J]. 武汉大学学报:工学版,2005,38(6):6-9,15.Xie Ping,Chen Guangcai,Xia Jun. Hydrological frequency calculation principle of inconsistent annual runoff series under changing environments[J].Engineering Journal of Wuhan University,2005,38(6):6-9,15(in Chinese).
[12] 谢 平,陈广才,雷红富,等. 水文变异诊断系统[J]. 水力发电学报,2010,29(1):85-91.Xie Ping,Chen Guangcai,Lei Hongfu,et al. Hydrological alteration diagnosis system[J].Journal of Hydroelectric Engineering,2010,29(1):85-91(in Chinese).
[13] 谢 云. 模拟退火算法的原理及实现[J]. 高等学校计算数学学报,1999(3):212-218.Xie Yun. Principle and realization of the simulated annealing algorithm[J].Numerical Mathematics A Journal of Chinese University,1999(3):212-218(in Chinese).
