思维导图在自动控制原理教学中的应用

2013-11-27李剑锋

中国教育技术装备 2013年32期

◆李剑锋

分析思维导图在自动控制原理教学中的具体应用。教学实践证明，基于思维导图的教学方法，提高了学生思维能力和主动性，加深了学生对基本概念和原理的理解，从而提高了教学质量。

1 引言

近几十年来，随着电子计算机的发展和应用，在宇宙航行、机器人控制、导弹制导以及核动力等高科技领域中，自动控制技术具有越来越重要的作用。自动控制技术的应用范围现已扩展到生物、医学、环境、经济管理和其他社会生活领域中，自动控制已经成为现代社会活动中不可或缺的部分。自动控制原理课程是高校电类、机械类及相关专业的一门重要专业基础课，是本科生后续课程和研究生课程的基础，在专业课程体系中占有重要地位[1-2]。自动控制原理概念多且抽象，公式较多，且要推理数学公式，整个课程系统性强。运用传统的板书和多媒体很难达到教学的目的，为了达到教学的目的和效果，在自动控制原理教学中引入思维导图，从而激发学生学习自动控制原理的兴趣，提高教学质量。

2 思维导图

思维导图[3-4]（Mind Maps）是由英国的托尼·博赞（托尼·布詹）于1970年代提出的一种辅助思考工具。思维导图通过在平面上的一个主题出发画出相关联的对象，像一个心脏及其周边的血管图，故又称为“心智图”。

思维导图既简单又极其有效，是一种革命性的思维工具。思维导图运用图文并重的技巧，把各级主题的关系用相互隶属与相关的层级图表现出来，把主题关键词与图像、颜色等建立记忆链接。思维导图充分运用左右脑的机能，利用记忆、阅读、思维的规律，协助人们在科学与艺术、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能。思维导图因此具有人类思维的强大功能。

思维导图是一种将放射性思考具体化的方法。放射性思考是人类大脑的自然思考方式，每一种进入大脑的资料，不论是感觉、记忆或是想法（包括文字、数字、符码、食物、香气、线条、颜色、意象、节奏、音符等），都可以成为一个思考中心，并由此中心向外发散出成千上万的关节点，每一个关节点代表与中心主题的一个连结，而每一个连结又可以成为另一个中心主题，再向外发散出成千上万的关节点，呈现出放射性立体结构。而这些关节的连结可以视为一个人的记忆，也就是个人数据库。

人类从一出生即开始累积这些庞大且复杂的数据库，大脑惊人的储存能力使人们累积了大量的资料，经由思维导图的放射性思考方法，除了加速资料的累积量外，更多的是将数据依据彼此间的关联性分层分类管理，使资料的储存、管理及应用因更有系统化而提高大脑运作的效率。同时，思维导图最善用左右脑的功能，藉由颜色、图像、符码的使用，不但可以协助人们记忆，增进创造力，也让其更轻松有趣，且具有个人特色及多面性。

3 思维导图在自动控制原理教学中的应用

利用思维导图引入课程学习和认知事物过程一般都是感知—分析—综合。先对学习的内容自动控制原理有一个整体的全面的认识，通过思维导图这个工具绘制自动控制原理的整体的脉络图。通过思维导图感知认识这门课程，直观认识课程的各个知识点，然后分析各个知识点之间的联系，再通过学习课程达到全面认识整个课程体系。

自动控制原理课程介绍了自动控制的基本概念，控制系统在时域和复域中的数学模型及其结构和信号流图；阐述了线性控制系统的时域分析法、根轨迹法、频域分析法以及校正和设计等方法；详细地讨论了线性离散系统的基础理论、数学模型、稳定性及稳态误差、动态性能分析以及数字校正等问题；在非线性控制系统的分析方面，给出相平面和描述函数的方法。

通过图1可以使学生对自动控制原理课程框架有一个全面的认识。

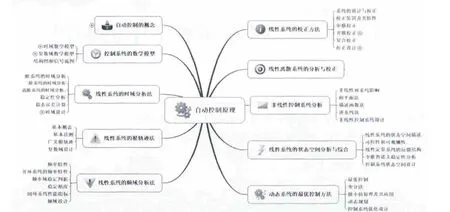
图1 自动控制原理课程的思维导图

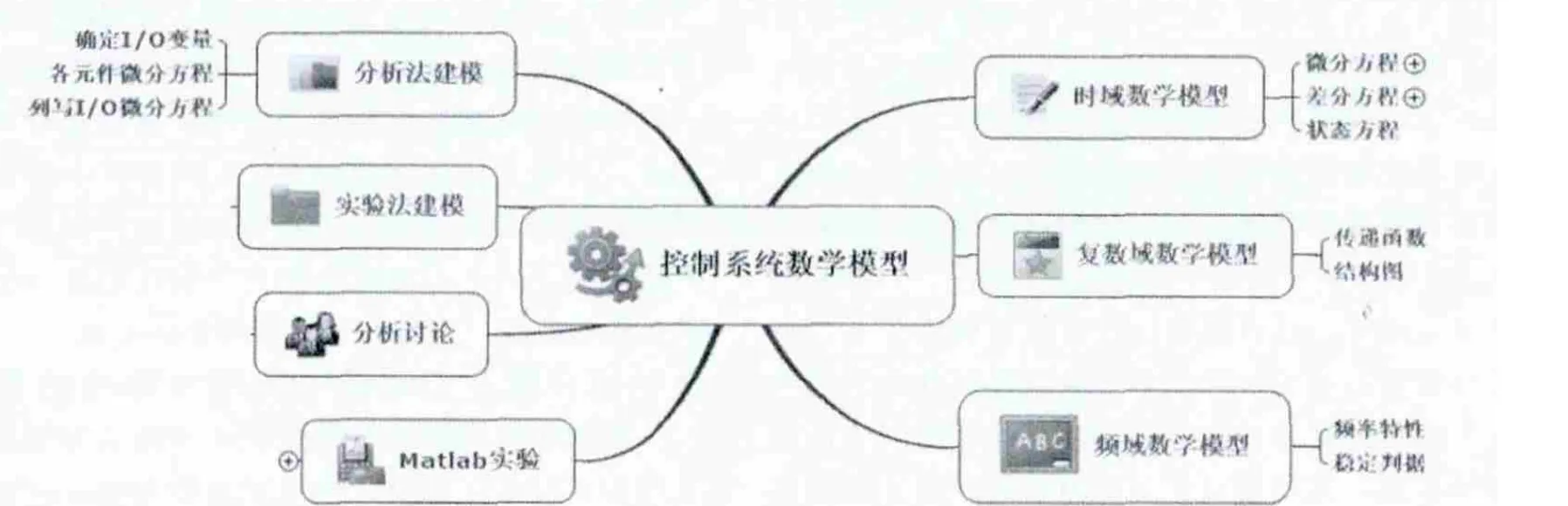
图2 控制系统数学模型的思维导图

建立控制系统的数学模型的思维导图思维导图以放射性思考模式为基础的收放自如方式，除了提供一个正确而快速的学习方法与工具外，运用在创意的联想与收敛、项目企划、问题解决与分析、会议管理等方面，往往产生令人惊喜的效果。它是一种展现个人智力潜能极致的方法，将可提升思考技巧，大幅增进记忆力、组织力与创造力。在控制系统的分析和设计中，首先要建立控制系统的数学模型。控制系统的数学模型是描述系统内部变量（或物理量）直接关系的数学表达式。在静态条件下，即变量各阶导数为零，描述各变量之间关系的代数方程叫静态数学模型。描述各变量直接的微分方程叫动态数学模型。建立控制系统数学模型的思维导图，可以将与数学模型相关联的知识点展现出来。思维导图运用图文并茂的技巧，开启人类大脑的无限潜能。思维导图充分运用左右脑的机能，协助人们在科学与艺术、逻辑与想象之间平衡发展。

图2是控制系统数学模型的思维导图，从思维导图可以直观地看出，控制系统数学模型的建模方法有分析法和实验法。实验法是人为地给系统施加某种测试信号，记录系统的输出响应，并用适当的数学模型去逼近，又称系统辨识。分析法建模是对控制系统的各部分的运动机理进行分析，根据系统依据的物理规律和化学规律分别列写相应的方程。也就是确定控制系统的输入输出变量，列写各元件的微分方程，消去中间变量，写出输入输出变量的微分方程。控制系统的数学模型形式在时域内有微分方程、差分方程、状态方程；在复数域有传递函数、结构图。频域内有频率特性。通过思维导图把控制系统数学模型的各个知识点有机地连接起来，在教学过程中，学生容易理解和掌握知识点的关系。