基于FPGA的实时CMOS视频图像预处理系统

徐 渊，周清海，张 智，朱明程

深圳大学信息工程学院EDA技术中心，深圳518060

在全景视频、高清监控、机器视觉及网络摄像等数字视频图像应用领域，视频图像的实时处理速度要求越来越高.传统的视频图像处理模式——电荷藕合器件(charge coupled device，CCD)+图像格式转换芯片+数字信号处理(digital signal processing，DSP)，已不适应上述领域的发展要求［1］.FPGA相对于DSP，具有电路设计灵活、并行处理及速度高的特点，特别适合这种高度、大数据量、算法复杂度不高的图像预处理系统［2-3］.因此使用FPGA+CMOS模式的实现图像预处理，成为图像实时采集处理系统实现的一种趋势［4］.

本研究针对CMOS传感器的特点，提出一种面向FPGA实现的视频图像预处理系统，并给出该系统在Xilinx SP605开发板配合MT9P031 CMOS传感器的硬件平台上的实验结果.

1 预处理系统的模块

基于FPGA的CMOS实时预处理系统主要实现模块架构如图1.首先，由I2C模块对CMOS图像传感器进行寄存器配置;然后，CMOS图像数据被送入FPGA图像预处理系统进行色彩插值、自动白平衡、色彩校正和伽马校正［5］;作为一个完整的系统，该预处理系统还需具备DDR存储器的接口对处理后的图像进行缓存，并通过VGA接口显示或直接写入存储器中用于存储和后续处理.

1.1 色彩插值

CMOS传感器的彩色成像是在黑白图像传感器的基础上，通过增加彩色滤波阵列(color filter array，CFA)来获得颜色分量.由于Bayer模式的CFA具有良好的彩色信号感光性及色彩复原性［6］，因而成为最常用的CFA.本研究只对该模式的CFA CMOS传感器进行讨论.

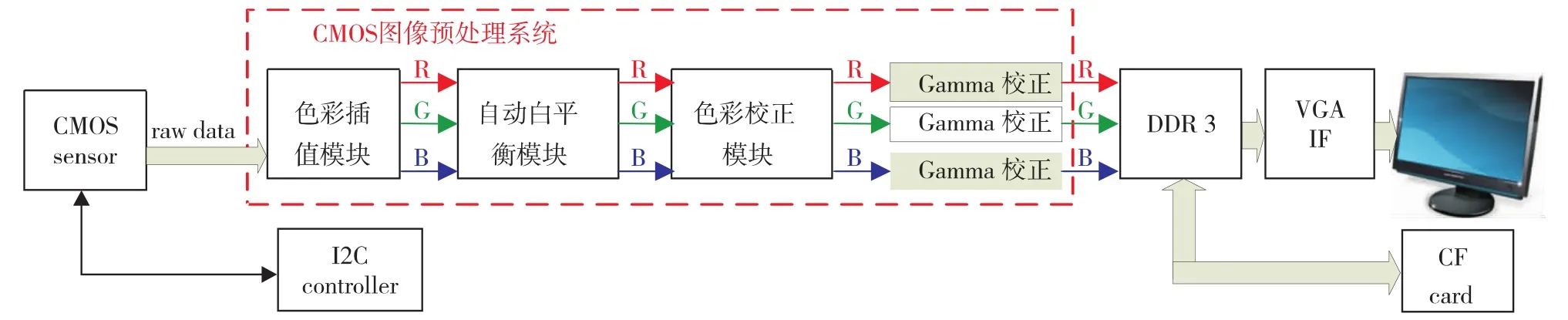
图1 CMOS实时预处理系统Fig.1 CMOS pre-processing system

生成彩色图像需R、G和B 3个颜色分量.其中，R为红色分量;G为绿色分量;B为蓝色分量.然而，在Bayer模式下，每个点仅一个颜色分量，其他颜色分量需由邻域点生成.通过邻域点生成欠缺的两种颜色分量的过程即色彩插值(color interpolation)［7］.在数字成像系统中，色彩插值的优劣，决定了从CFA输出的图像矩阵中重构图像质量的好坏［8］.色彩插值方法中，最近邻域法最简单，但重构图像质量最差;信号相关性插值法和双线性法［9］实现难度适中，效果优于邻域法;而更复杂的方法，如神经网络法［10］等，可取得质量更好的图像，但硬件资源的消耗与实现的复杂度亦增大.以下我们讨论双线性法与信号相关性插值.

图2是双线性及信号相关性插值的示例［8-9］.在图2(a)中，中心点B5仅含B分量，需还原R和G分量，即R5和G5.双线性法还原公式为

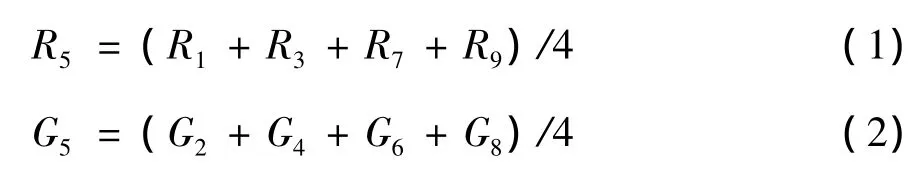
Pei等［11］提出信号相关性插值法，在双线性法的基础上引入辅助量KR和KB，如图2(b).由式(3)～式(8)可计算相应的辅助量

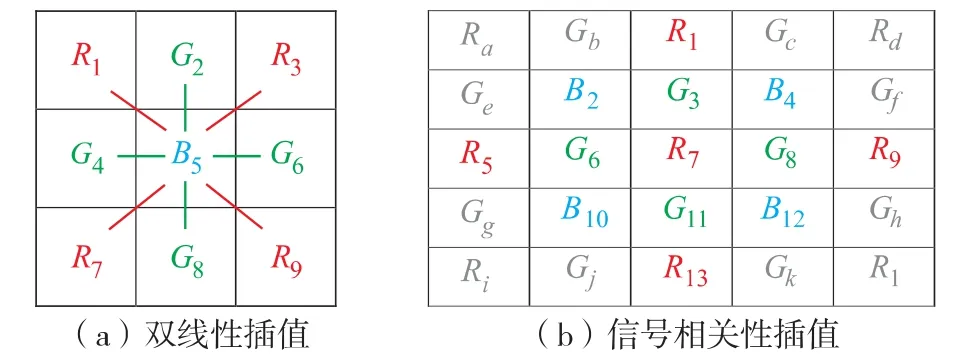
图2 双线性及信号相关性插值示例Fig.2 Bilinear＆signal correlation interpolation diagram

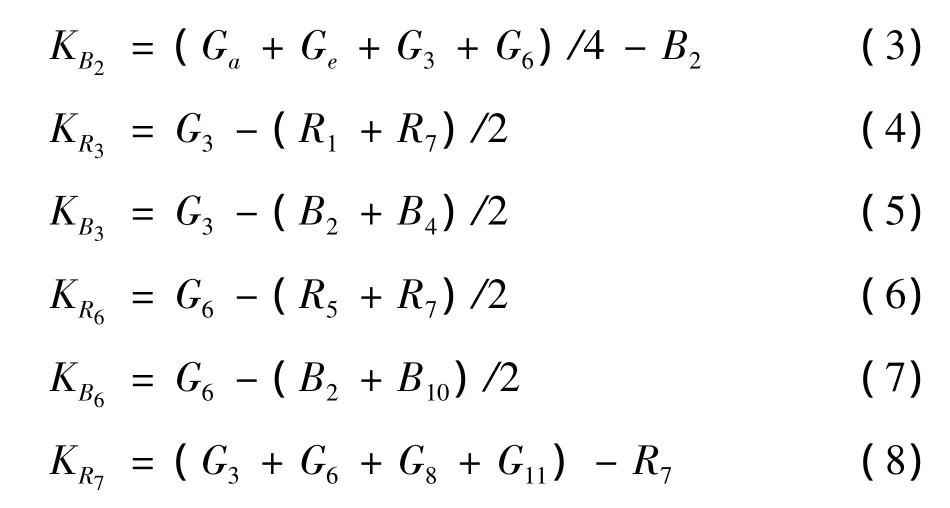
再通过式(9)～式(12)对B2和R7进行插值计算

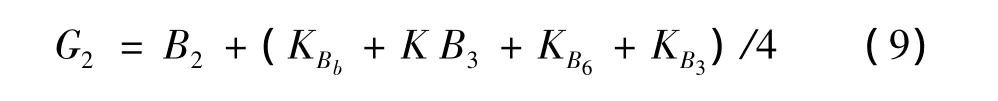
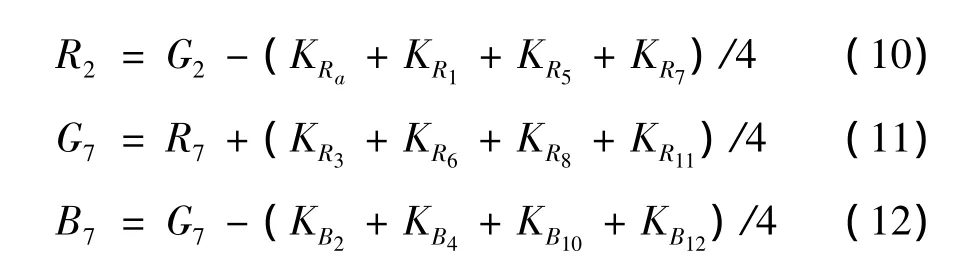
其中，KB2、KR3、KB3、KR6、KB6和KR7为辅助量;式(3)～式(7)中等号右侧的变量，及式(9)～式(12)中B2、G2、R7和G7为图2(b)中对应点的值.

常用的边界处理算法都较复杂，为此引入一种简便有效的边界保持方法，在求辅助量KR和KB均值前，去掉最大值和最小值，则G7生成式变成

其中，KRmax=max{KR3，KR6，KR8，KR11};KRmin=min{KR3，KR6，KR8，KR11}.

对Kodak的测试图像lighthouse，分别采用相关性插值、双线性插值、相关性与边界保持插值、双线性与边界保持插值进行测试.通过比较各重构图像的平均峰值信噪比(peak signal to noise ratio，PSNR)来对比各算法效果，结果如表1.

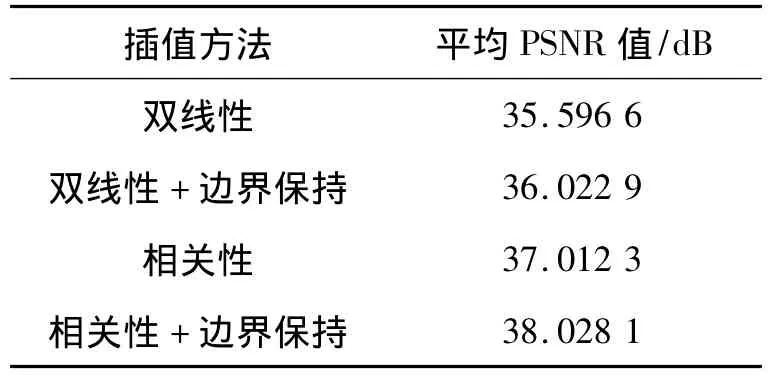
表1 几种方法平均PSNR对比Table1 PSNR comparison

由表1可见，相关性与边界保持插值方法产生的图像与原图最接近，计得的平均PSNR值最高.因此，在插值模块中，本研究最终选用此算法.

由图2(b)可知，信号相关性插值至少需同时提供5×5的图像数据块，即需一个5×5的图像窗口生成模块来提供数据.为减少对FPGA芯片内有限片内存储器的使用，本研究改进了片内存储器的使用方法.用Ram0—Ram4代替移位寄存器构成的行缓冲0—4行缓冲，并用如图3的状态机对其进行控制.其中，rdata0—rdata4分别对应此状态下Ram0—Ram4的读数据，Data0—Data4为最终窗口输出的5个数据，Data0始终连接窗口输入Data_in.行结束信号Line_end为状态跳转条件信号.各Ram的读写地址相同，其范围都是0～N(N为图像列宽减1).

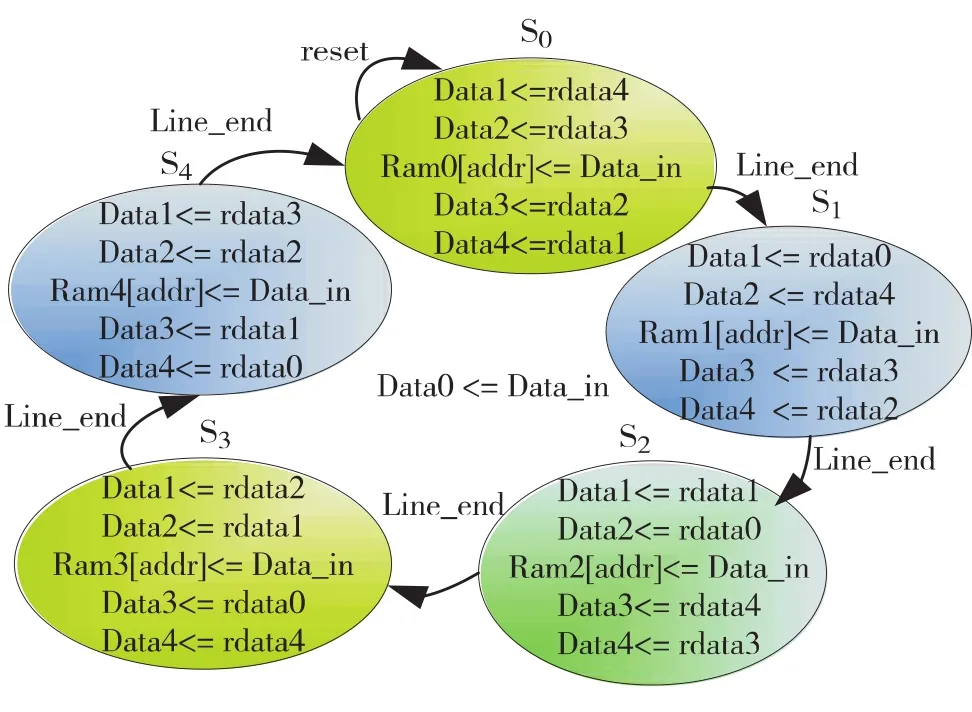
图3 改进的图像窗口控制状态图Fig.3 Improved image window control FSM

1.2 色彩校正

1.2.1 自动白平衡

通过白平衡模块，可校正由不同色温所引起的色差，使物体再现其本来颜色.常用的白平衡方法有灰色世界法［12］和神经网络法［13］(实现复杂，资源消耗大，不适用于FPGA芯片).灰色世界法的实现过程为，通过增益调整使图像的3个分量的平均值Rav=Gav=Bav，具体步骤为:

1)计算图像中的3个分量均值

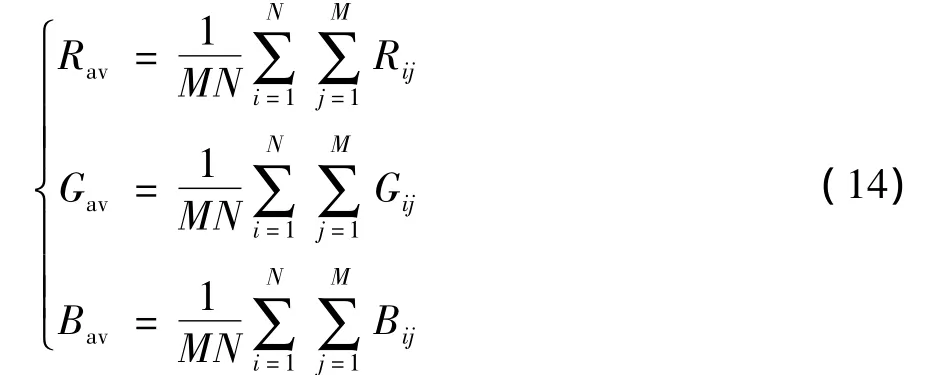
2)R、G和B分量的增益分别为

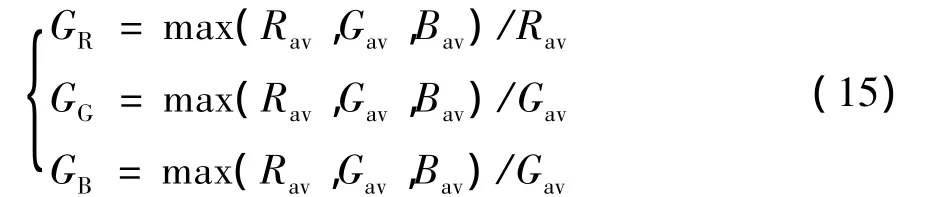
3)处理

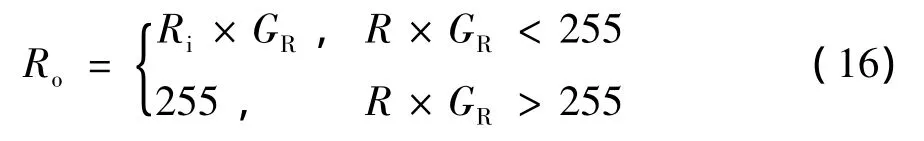
其中，Ri和Ro分别为输入与输出的R分量.对于G和B分量可做同样处理.

将用当前帧计算得到的增益近似为后1帧的增益，为能在1帧时间内完成统计和增益计算，不统计帧图像中所有数据，仅统计选定区域内固定的数目.在计算均值时，可用右移位来实现除法，而在计算增益时，可降低除法器的位宽，以节省资源，提高速度.

1.2.2 色彩校正

未经色彩校正的图像与真实颜色间的偏差被称为颜色失真.文献［14］介绍了几种常用色彩校正方法，其中矩阵校正法运算简单，易于硬件实现.本研究根据FPGA芯片特点，采用矩阵校正法，在RGB空间进行色彩校正.校正公式为

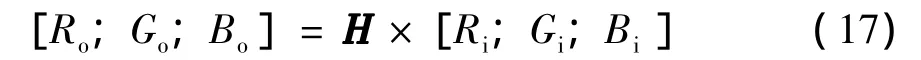
其中，Ri、Gi、Bi和Ro、Go、Bo分别为校正前后的RGB值;H为3×3校正矩阵.使色差最小化的H，即为所求校正矩阵.

RGB空间任意两个颜色(R1，G1，B1)和(R2，G2，B2)之间的色差公式为

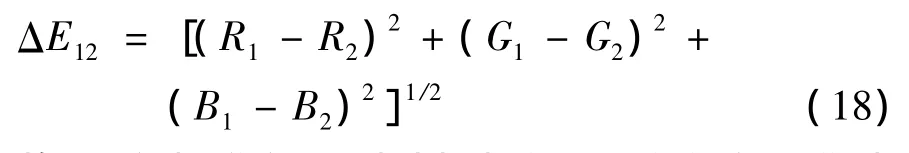
将24色标准色彩测试标板的24个颜色，作为颜色取样数据对象，来获取校正矩阵.校正过程为

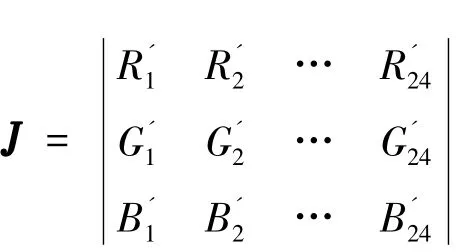
其中，为校正后24个颜色的RGB值为24个颜色的测试RGB值;为所求校正矩阵.

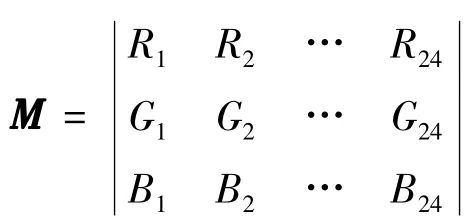
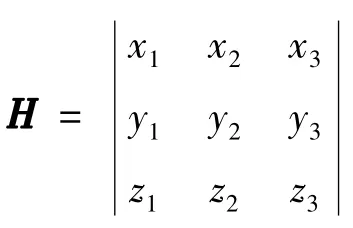
要使24个颜色的色差最小，需使

ΔR21+ΔG21+ΔB21+… +ΔR224+ΔG224+ΔB224最小，而该多项式等于

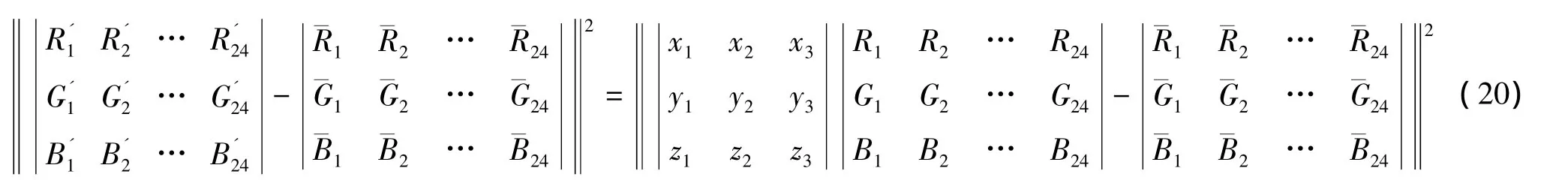
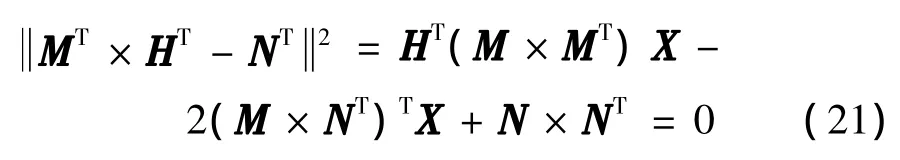
可得X=(M×MT)TM×NT，故校正矩阵为

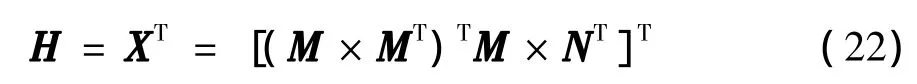
用近似方法使N得到标准色板上的相应值.在相同光照条件下，用一台标准相机，以手动模式拍摄标准色板，并以其24个颜色的均值作为标准RGB颜色矩阵N.然后使用CMOS传感器抓取测试图像的24色RGB值，作为测试矩阵M.由式(21)计得校正矩阵H后，用该矩阵校正测试矩阵M，并得到N'.最后，分别计算M、N'与N之间的色差值.

图4为校正前后图像与标准图像色彩对比，图5为校正前后色差对比.由图4可见，修正色彩比未修正色彩更接近参照色彩.由图5也可发现，修正后的色彩更佳.

用上述方法求得的校正矩阵为

为便于硬件实现，放大64倍后取整，得

用H1矩阵与CMOS采集的图像数据相乘，再将所得矩阵的各二进制元素进行6 bit的右移运算，得到色彩校正后的色彩图像.

1.2.3 伽马校正

由于电子器件如CMOS传感器和显示器等的光电响应有非线性特性，因此必须对图像进行伽马校正.校正过程为 S=X1/γ.其中，γ 取值 1.8 ～2.5.对于此非线性校正过程，本研究采用分段线性伽马校正法，即用分段线性函数逼近非线性伽马校正曲线，如图6(a).其中，y(x)是关于输出亮度x的校正函数，可使用分段点间的直线迫近真实曲线y(x).由图6(b)，一段以a和b为分段点的线段星映射为

图4 色彩校正结果Fig.4 Color correction result

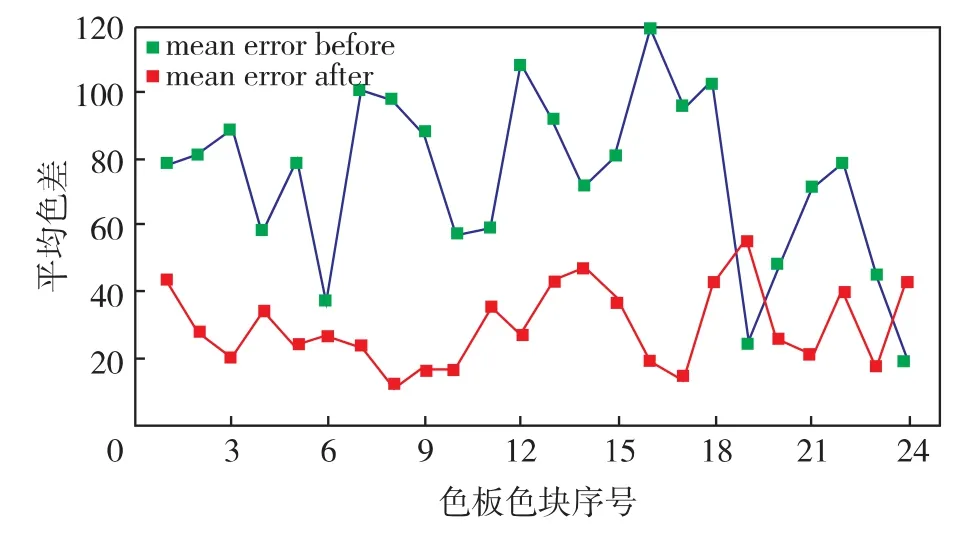
图5 色彩校正前后与标准图像的色差对比Fig.5 Chromatic aberration comparison before and after color correction

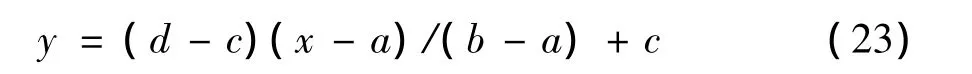
其中，x为a和b之间的图像亮度;c为起始位置纵坐标;d为结束点横坐标.

令d-c=n，b-a=m，则得最终的实现方程为

根据Weber Fechner法则［15］，人以亮度L的比值ΔL/L为视觉刺激量的，在特定环境亮度下，人眼所能够识别亮度的最低值，约等于该比值的2%.考虑到人类的视觉特性，可得

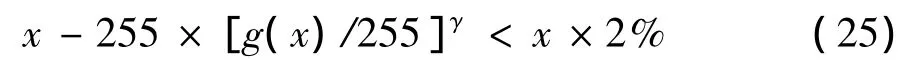
其中，x是理想情况下，系统响应为线性时的输出;g(x)为用线性法得到的转换后的值.整理后得

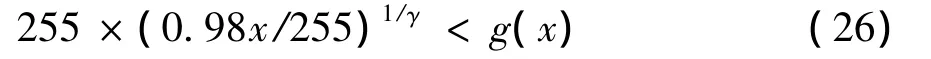
利用式(26)，只要保持m为2的幂次方，就可在FPGA实现中避免除法.以0为起始点，2n为步长，可得一系列分段点为0，2，4，….

综上可最终确定 x=［0，4，8，16，32，48，64，128，192，256］作为分段点.对0～255实行9段分区，如图6(c).

针对不同的γ，由y=x1/γ代入确定的x求得相应的分段端点的y值;再根据图6(c)和前面的定义，就可求得c、m、n和a的对应值，并最终实现分段线性伽马校正.

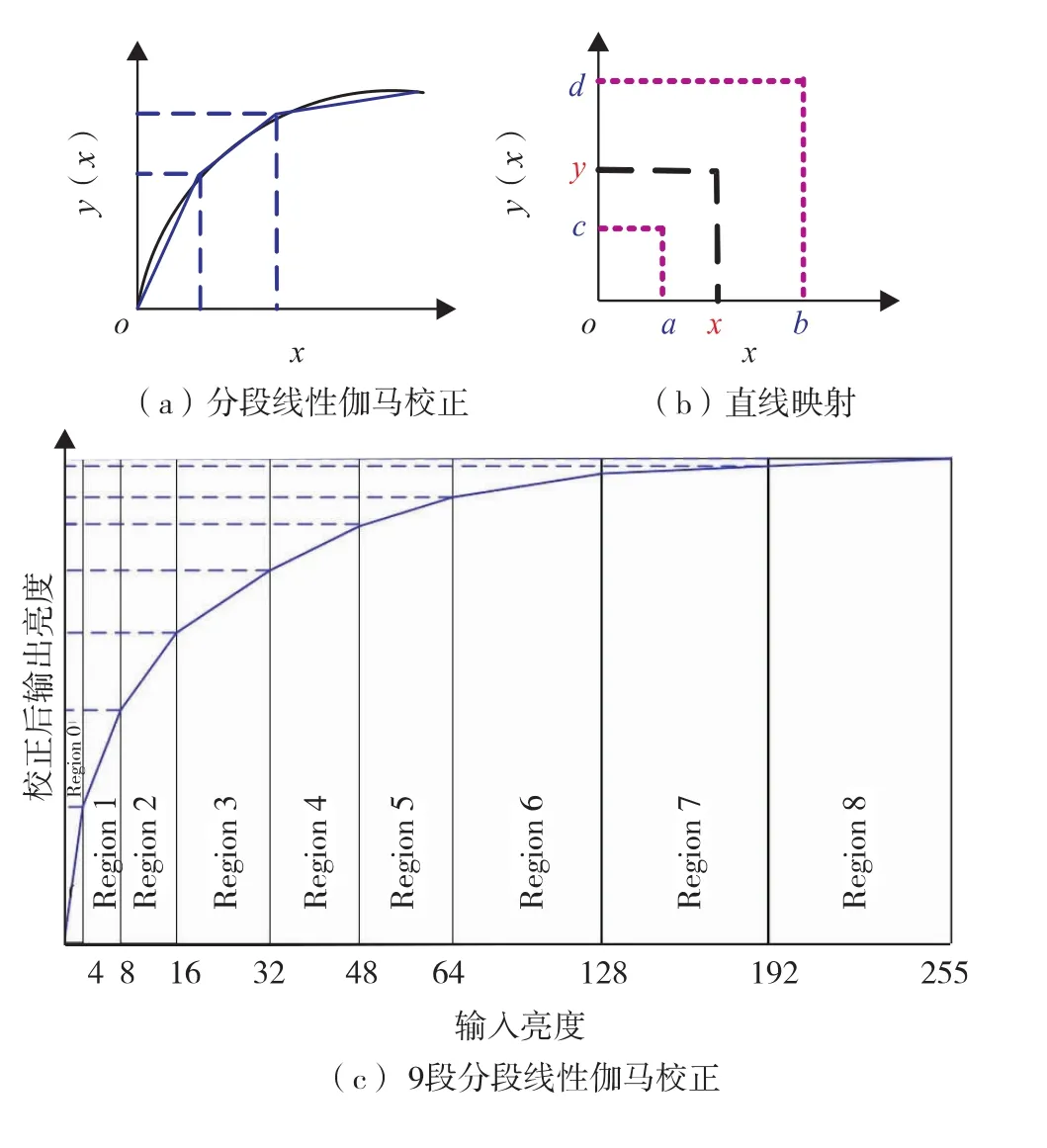
图6 分段线性伽马校正、直线映射与9段分段线性伽马校正Fig.6 Segmented liner Gamma correction，liner mapping and 9-segmented liner Gamma correction

2 子模块硬件结构

图7(a)为相关性边界保持插值模块.数据从Data in输入，按照1.1节所述算法处理后，输出Data_out.图7(b)为自动白平衡模块.用于控制RGB 3个分量均值统计部分的起始.该信号有效时，将计算得到的3个分量增益存入增益寄存，供后一帧图像白平衡运算使用.图7(c)为色彩校正电路.RGB 3路色彩分别输入校正系统，经矩阵校正后再分别输出，供给下一系统使用.图7(d)为分段线性伽马校正电路.

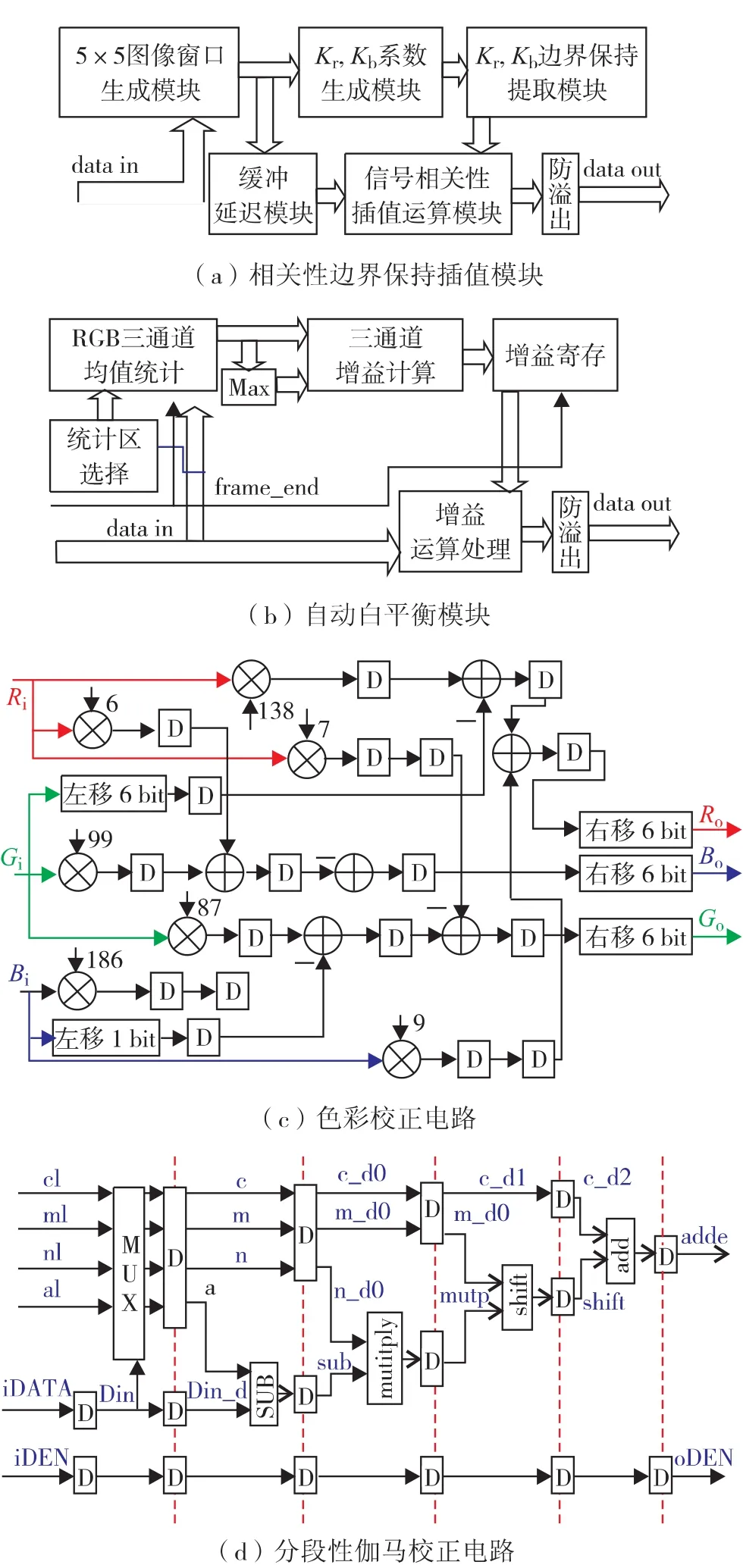
图7 系统各子模块结构Fig.7 Sub-module of the system

3 FPGA实现

本设计在Xilinx SP605开发板和MT9P031 CMOS图像传感器上，实现整个系统.表2为该传感器主要资源使用情况.从表2可见，所需资源不多，有利于整个系统的成本控制.

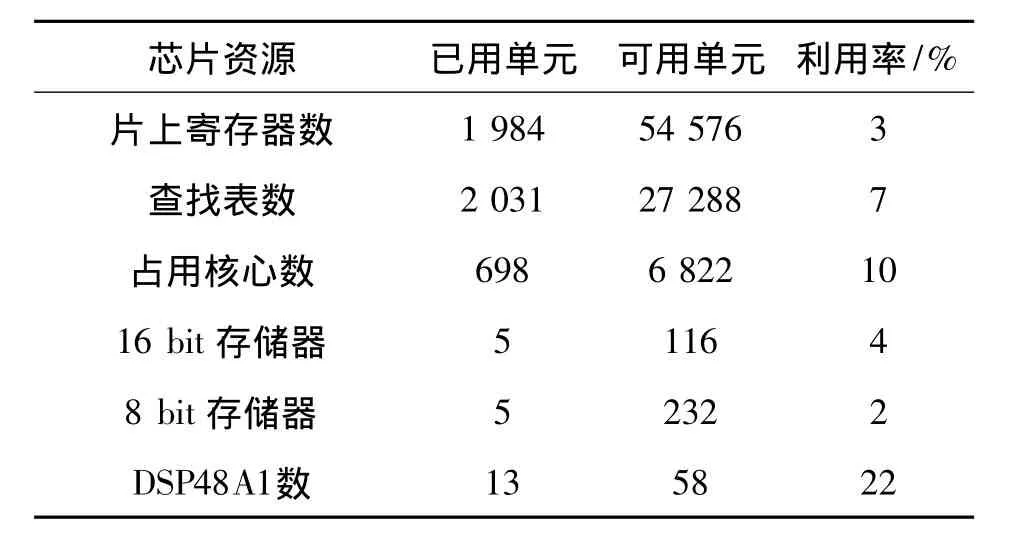
表2 预处理系统PAR后的资源利用率Table2 Pre-process system resource utilization after P＆R

该系统最高频率达120.758 MHz，处理速度是720P@60fps视频流所需带宽的2.29倍;对于高清1080P(1920×1080像素)的图像，处理速度为61帧/秒，远高于1080P@30fps标准的高清视频流.对720P@60fps的视频测试结果显示，视频流畅.图8为实验实测图，视频图像画面与真实物体颜色相差较小，画面连续无卡顿感，达到预计要求.

图8 实验实测Fig.8 Experiment result

结 语

本研究针对实时CMOS视频图像的预处理的要求，对色彩插值、白平衡、色彩校正和伽马校正等模块进行研究，针对硬件实现的特点，对算法进行优化，提出适于PFGA实现的电路结构，并在单颗PFGA芯片实现整个系统.测试结果表明，系统输出图像质量良好，且处理速度快.该设计结构简单，所耗芯片资源较少，可应用于高清监控、机器视觉及网络摄像等系统.

/References:

［1］Hamza D，Pahlevaninezhad M，Jain P K.Implementation of a novel digital active EMI technique in a DSP-based DC-DC digital controller used in electric vehicle(EV)［J］.IEEE Transactions on Power Electronics，2013，28(7):3126-3137.

［2］Mariangela Genovese，Ettore Napoli.ASIC and FPGA implementation of the Gaussian mixture model algorithm for real-time segmentation of high definition video ［J］.IEEE Transactions on Very Large Scale Integration(VLSI)Systems，2013，PP(99):doi:10.1109/TVLSI.2013.2249295.

［3］Chen Biwei，Liang Zhiyi，Wang Yanxin，et al.Design of a high speed CMOS imaging system based on FPGA［J］.Computer Measurement＆ Control，2012，20(5):1397-1400.(in Chinese)陈必威，梁志毅，王延新，等.基于FPGA的高帧速CMOS成像系统设计 ［J］.计算机测量与控制，2012，20(5):1397-1400.

［4］Ding Haojie，Liu Jingbiao，Sheng Qinghu.Design of video acquisition system based on CMOS image sensor［J］.Modern Electronics Technique，2012，35(14):178-188.(in Chinese)丁昊杰，刘敬彪，盛庆华.基于CMOS图像传感器的视频采集系统设计 ［J］.现代电子技术，2012，35(14):178-188.

［5］Tai Yonghang，Yun Lijun，Shi Junsheng，et al.A method for AM-OLED gamma correction ［J］.Opto-E-lectronic Engineering Jan，2012，39(1):131-134.

［6］Bayer B E.Color imaging array:US，3971065 ［P］.1976-07-20.

［7］Jeon G，Dubois E.Demosaicking of noisy bayer-sampled color images with least-squares luma-chroma demultiplexing and noise level estimation ［J］.IEEE Transactions on Image Procesing，2013，22(1):146-156.

［8］Hua Lei，Xie Lei，Chen Huifang.A color interpolation algorithm for Bayer pattern digital cameras based on green components and color difference space［C］//International Conference on Progress in Informatics and Computing.Shanghai(China):IEEE Press，2010，2:791-795.

［9］Zhao Huang，Peng Yong.Bilinear interpolation algorithm optimization and application ［J］. TV Engineering，2012，36(17):30-32.(in Chinese)赵 煌，彭 勇.双线性插值算法的优化及其应用［J］.电视技术，2012，36(17):30-32.

［10］Go J，Lee C H.Interpolation using neural network for digital still cameras［C］//International Conference on Consumer Electronics.Los Angles(USA):IEEE Press，2000:176-177.

［11］Pei S C，Tam I.Effective color interpolation in CCD color filter arrays using signal correlation［J］.IEEE Transactions on Circuits Systems for Video Technology，2003，13(6):503-513.

［12］Yan Ge.Design of CMOS Image Sensor Automatic White Balance Digital Process Circuit［D］.Tianjin:Tianjin U-niversity，2009.(in Chinese).闫 格.CMOS图像传感器白平衡数字处理电路设计［D］.天津:天津大学，2009.

［13］Liu Yucheng，Zhang Yingchao.Image colorimetry segmentation based on white balance algorithm ［J］.Computer Engineering，2012，38(20):195-196.(in Chinese)刘玉成，张颖超.基于白平衡算法的图像色度学分割［J］.计算机工程，2012，38(20):195-196.

［14］Xu Xiaozhao，Shen Lansun，Liu Changjiang.Color correction methods and application in image processing ［J］.Application Research of Computers，2008，25(8):2250-2254.(in Chinese)徐晓昭，沈兰荪，刘长江.颜色校正方法及其在图像处理中的应用［J］.计算机应用研究，2008，25(8):2250-2254.

［15］Ming Jun，Xu Huifang，Yang Yang.Research of space similarity analysis model with Weber-Fechner law ［J］.Journal of University of Science and Technology of China，2010，40(11):1148-1152.(in Chinese)明 军，许会芳，杨 杨.Weber-Fechner空间相似分解模型的研究［J］.中国科学技术大学学报，2010，40(11):1148-1152.