列车车站停车的启发式自学习算法及仿真
2013-11-26陈德旺
陈 荣,陈德旺
(北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
近几年,随着地铁在城市公共交通中高效、便捷、安全的优势日趋显著,中国各大城市也相应加快其建设。新建的地铁车站都加装了屏蔽门以防止乘客在换乘时发生跌落的危险发生,同时也对列车精确停车提出了更高的要求。然而,从已投入运行的交通系统来看,列车进站停车位置不精确的问题时有发生。此类问题不仅影响列车的正常运营,而且存在严重的安全隐患。如:对于安装有屏蔽门的车站,列车停车不精确将会导致车门与屏蔽门无法正确对位[1],乘客无法正常换乘。地铁列车进站停车的精确性问题涉及列车制动系统控制、外界环境及线路条件等诸多因素的影响。主要有以下3个方面:(1)列车制动系统的延时和时间常数的不同。从列车自动列车控制(ATC)系统下达指令到列车制动系统的传输延时对于列车精确停车有很大的影响,并且不同的列车的传输延时也不同。(2)列车制动性能的变化。地铁列车的基础制动装置中闸瓦摩擦系数受环境温度、湿度和使用时间的影响,导致列车制动时制动力与制动指令需求有一定的差距。(3)基本阻力的变化。列车运行过程中,车体所受的阻力会随着车速而变化,其阻力来自轴承阻力、滚动阻力、滑动阻力、冲击与振动阻力以及空气阻力的共同作用。
在当前的地铁ATC系统中,主要采用传统的PID控制器跟踪目标曲线的方法。PID控制器主要运用于传统的工业控制,取得了较好的控制效果,但对于复杂多变的列车控制,其控制效果并不是很理想。因为停车阶段只有制动和惰行两种工况,所以对于PID控制有较大的限制。国内外有一些专家已经将智能控制方法运用于列车控制。
K. Yoshimoto将模糊推理理论列车自动停车控制,将停车分为多个区段以便运用不同的推理规则[2~3]。侯忠生提出了终端迭代学习停车控制,利用大量的停车历史数据优化控制参数[4]。贺广宇提出了利用线性二次型最优控制理论实现列车精确停车[5]。我们曾提出了两种基于列车停车数据的动力学模型[6],并且将软计算方法引入了停车控制[7]。这些方法都是属于离线控制。周骥提出将机器学习方法运用于列车控制[8]。以上方法在仿真过程中均假设列车定位信息是精确的,而且也没有考虑制动系统所受的干扰以及外界环境因素。这些干扰影响在工程中是无法避免的。应答器在ETCS和CTCS-3中都是极其关键的设备,地铁中也在站内安装以辅助列车定位[9]。这些精确的定位信息对于列车自动停车控制有着重要的价值[10],因此,针对以上的几种因素,提出启发式学习算法,该方法有更强的自学习能力、更接近实际应用。文章通过仿真测试分析其性能。
1 停车算法
在线学习精确停车算法包括:停车控制器、估计器和控制器,如图1所示。估计器的作用主要是通过精确的位置信息,通过预估获得下一时刻控制量,并输入停车控制器。停车控制器通过估计器的估计控制量和控制器前一时刻的控制量进行综合计算,输出补偿控制器以减小系统延时、外界环境的影响造成的制动误差。为了便于接下来的讨论,定义一个停车区域范围L如图2 所示,在这个区域里面有n个停车应答器,将其编号为S1,S2,…,Sn。将第1个应答器作为初始点,第n个应答器作为停车点。列车经过第i个应答器的速度为υi。受列车制动系统的限制,停车控制器的最大输出值为αMAX。

图1 学习算法模型框图
列车停车控制过程是一个以列车运行数据为输入,受到时变干扰影响的控制过程。一般情况下,可以表示为如下控制模型:
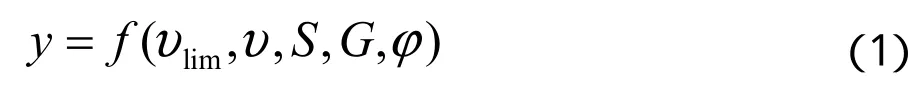
其中,υlim为限速信息,υ为列车速度信息,S为列车的定位信息,G为线路坡度信息, 为干扰,y为输出。
列车经过应答器时,可以收到精确的定位信息Si,根据列车当前速度可以由公式(2)计算得到当前理论制动率αEi,其中υt为0。经过下一个应答器时,根据公式(3)可以得到实际平均制动率αi,其中,Di为应答器之间的间距即Di=Si- Si+1,υi为经过第i个应答器的速度。由于前述3种因素的影响,αEi和αi之间存在着一定的偏差,记为 ∆αi。
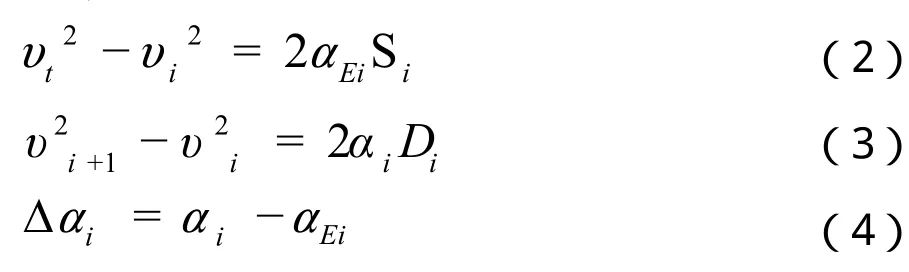
1.1 无学习停车控制算法
在列车停车过程中,如果不考虑干扰停车的因素影响,则每经过一次应答器均采用公式(2)计算获得的理论制动率输出。其控制模型如下:
1.2 固定学习率的启发式学习算法
在无学习停车控制基础之上,我们加入启发式学习算法作为输出控制的补偿。根据输出之间的偏差如公式(4),影响停车的干扰因素可以假设为平均分散至该停车过程,其均值为Δαi。基于以上的假设提出以固定学习率动态调整列车制动控制器的输出,模型如下所示:

该模型可以实时根据先前的控制信息动态调整输出,对干扰造成的影响有一定的补偿作用。
1.3 可变学习率的启发式学习算法
上述固定学习率的启发式学习算法,由于学习率固定不变,当应答器的间距不是以等距排列,或者列车速度发生变化后,其无法根据这些变化信息做出相应的调整。为了弥补这个不足,提出了可变学习率的模型如下:

根据停车驾驶经验我们可以知道,可变学习率与当前速度和应答器位置有如下关系:

该模型可以根据当前速度和应答器位置调整学习步长,相对固定学习率模型对线路情况有更好的适应能力。
以上所述的学习算法不需要知道列车模型,通过在线学习方式并根据实际运行参数自适应修正,减小这些因素的影响。能够很好的解决因不同列车的制动系统的响应不同和外界环境对于制动系统造成影响所带来的问题。这种利用应答器信息的在线学习修正误差方法的效果我们将会在以下仿真中加以验证。
2 列车和算法模型的建立
为了模拟列车在进站时各种因素的影响,使用Simulink工具箱搭建了列车系统仿真模型。整个系统包括输入模块、发生器模块、控制器模块、执行器模块、输出及显示模块5大部分。其中,输入模块根据实际需要输入可变信息;发生器模块的主要功能是模拟列车运行情况下的外界阻力及随机干扰,本文使用阻力公式:

其中,α=1.36×10-4,β=1.45×10-2,γ=1.244[11]。控制器模块主要根据发生器产生的信息,经过算法的计算得到列车控制量,并输出控制列车;执行器模块是模拟被控对象列车,主要包括:列车工况转换时的系统延时环节的模拟;输出及显示模块主要显示仿真运行的结果信息,包括:停车误差、控制器输出等。整体设计架构如图3 所示。
通过使用其提供的基本工具搭建了列车制动系统模型如图4所示。外界阻力模型等环节模拟对于停车控制的影响。

图3 列车运行系统模型框图
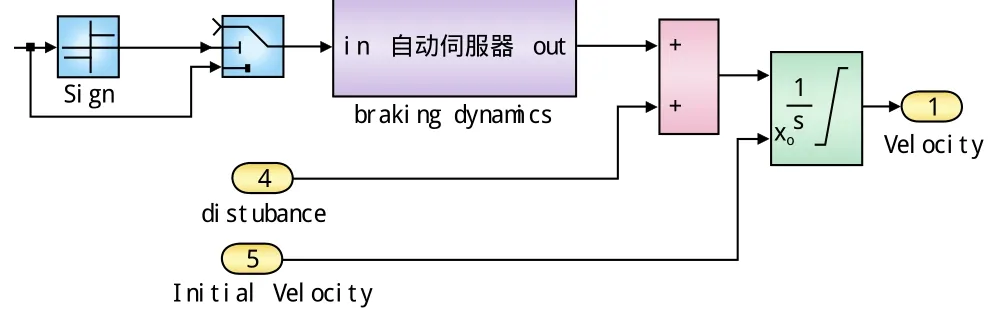
图4 列车制动系统模型
制动伺服器传递函数[12~13]为:
其中α0为基本制动力,Tp为时间常数,Td为制动系统延时。
3 仿真评估
为了模拟列车实际运行,选取北京亦庄地铁线路的亦庄文化园-万源街两站之间的线路数据作为仿真的输入信息,其包括:长度(1 280.5 m)、限速、坡度、应答器安装位置等。取前述停车区域长度L=102 m,车站安装5个停车应答器组,安装的位置分别距离停车点S1=102 m、S2=58 m、S3=13 m、S4=6 m和S5=0 m处。通过运动学公式及制动加速度限制条件(αmax≤α≤0,其中αmax= -1m/s2)可以理论计算得到进入该102 m区域的最大初始速度υmax约为14.28 m/s。但是列车制动系统有延时,需要有一定的裕度,否则保持以αmax制动也无法在停车点停下。根据实际运营数据可知,在列车进入车站前102 m,速度一般会低于40 km/h(约11.11 m/s)。
3.1 常规情况
在υ1=10 m/s,Td=0.6 s,Tp=0.4 s,α=1.36×10-4,β=1.45×10-2,γ=1.244情况下,PID算法如图5 、无学习算法、固定学习率算法及可变学习率算法的速度—位置和控制器输出—位置仿真图分别如图5~图8所示,其停车精度分别为:0.016 6 m、0.266 7 m、-0.007 4 m及0.043 3 m。,相对于PID控制算法,其它3种算法每经过一次应答器,控制器输出仅改变一次,所以整个停车过程控制器最多改变4次。但是在外界环境不变化的情况下,PID算法具有较高的停车精度。

图5 PID算法的常规情况仿真图

图6 无学习算法的常规情况仿真图
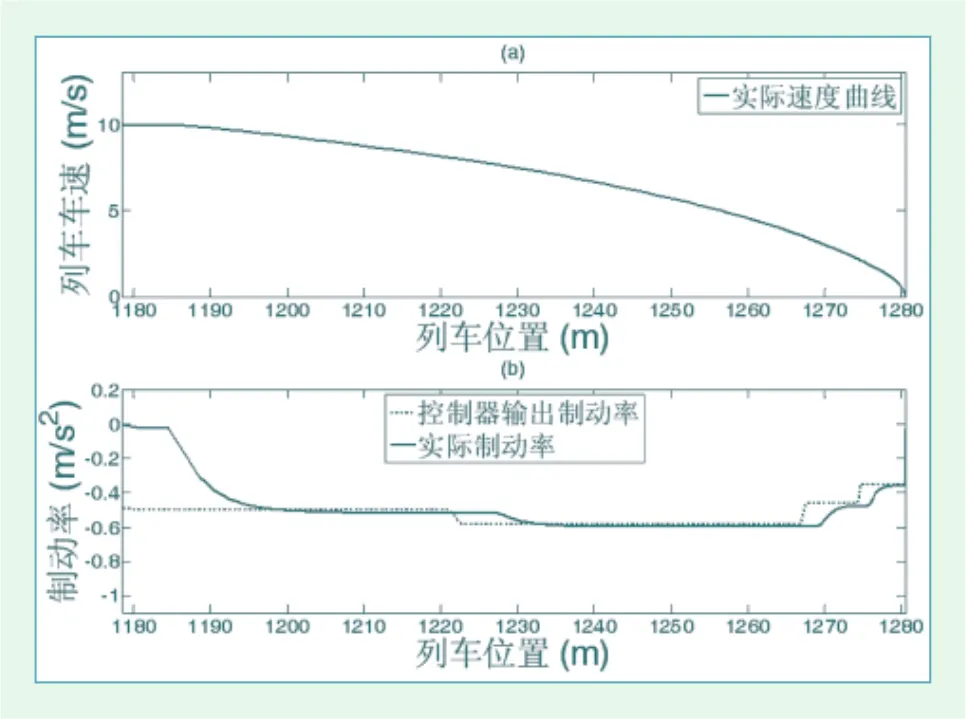
图7 固定学习率算法的常规情况仿真图
3.2 列车进站初始速度变化情况

图8 可变学习率算法的常规情况仿真图
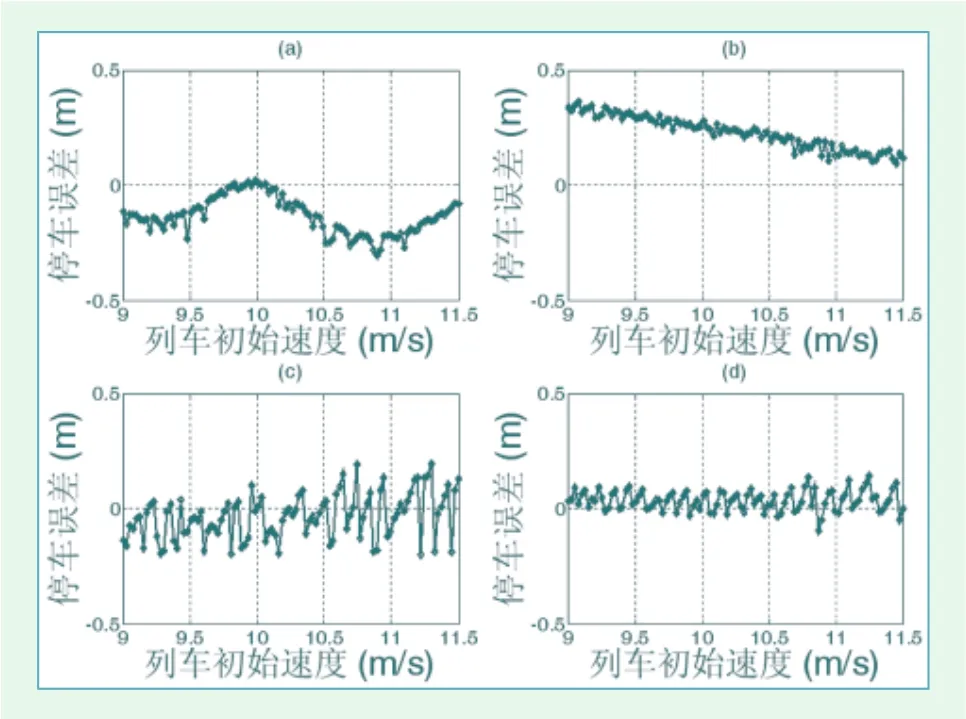
图9 初始速度变化条件下的停车误差
当进站初始速度υ1在9 m/s~11.5 m/s之间变化,其它参数保持不变时,经过100次仿真,每次变化间隔为0.025 m/s。图9 中停车误差变化。可以看出,在初始速度发生变化的情况下,PID算法会呈现一定规律的波动,而学习算法中,可变学习率(标准差为0.043 9 m)的波动相对固定学习率(标准差0.099 7 m)小。
3.3 列车制动系统延时变化情况
当制动系统延时Td以0.003 6 s为间隔在0.42 s~0.78 s之间变化仿真100次。图10中,a、b、c和d分别表示4种停车控制算法的停车误差。PID算法随着系统延时增大会导致停车精度降低。
3.4 4种方法比较
根据以上仿真实验,统计以下几项指标对比:常规情况下4种算法的停车精度,初始速度υ1变化、系统延时Td变化情况下的停车误差的绝对值的平均值(AAV),控制器输出改变次数。列出表格 1以便于比较。启发式学习算法相对于传统的PID算法在不同条件下的有更强的适应能力,可变学习率表现相对更好。并且控制器输出切换次数明显降低,有利于减少制动系统的损耗。

图10 系统时间延时变化条件下的停车误差

表1 仿真结果汇总
4 结束语
本文对所提出的启发式学习算法在初始速度变化和系统延时变化情况下进行仿真测试,结果显示该算法满足了列车停车精度的要求。对比传统PID算法,该方法停车误差在[-0.30 m 0.30 m]之间概率更大。此学习算法很好地解决由于进站初始速度变化、列车制动系统延时因素对停车误差的影响。并且该算法运算量很小,便于投入实际工程应用。
该算法目前采用较为简单的启发式学习方式,在今后工作中,将会深入研究其他学习算法在列车停车过程控制的应用。
[1]刘金叶. 运营线路加装屏蔽门后列车停站精度偏差分析及调整对策[J]. 城市轨道交通研究,2009,12(1):44-47.
[2]S. Yasunobu, S. Miyamoto, H. Ihara. A Fuzzy Control for Train Automatic Stop Control[J]. Trans. of the Society of Instrument and Control Engineers, 2002, 2(1):1-8.
[3]Seiji Yasunobu, Shoji Miyamoto. Automatic Train Operation System by Predictive Fuzzy Control[J]. Industrial Applications of Fuzzy Control,1985, 1(18): 1-18.
[4]Z. S. Hou, Y. Wang, C. k. Yin. Terminal Iterative Learning Control based Station Stop Control of a Train[J]. International Journal of Control, 2009, 84(7): 1263-1274.
[5]贺广宇.基于LQR的列车精确停车控制算法研究[D]. 北京:北京交通大学,2009.
[6]陈德旺,唐 涛,郜春海.城轨列车在车站停车误差估计模型与在线学习算法的研究[J].中国铁道科学,2010,31(6):122-127.
[7]D. W. Chen, C. H. Gao. Soft Com-puting Methods Applied to Train Station Parking in Urban Rail Transit[J]. Applied Soft Computing, 2012, 12(2): 759-767.
[8]周 骥,陈德旺.机器学习在列车精确停车问题的应用[J]. 计算机工程与应用,2010,46(25):226-230.
[9]J. H. Beak. The Study on Train-Separation Control Safety BrakingModel Technology Using Balise for Conventional Lines[C].Telecommunications Energy Conference, 2009:1-4.
[10]M. A. Sandidzadeh, A. Khodadadi. Optimization of Balise Placement in a Railway Track Using a Vehicle-an Odometer and Genetic Algorithm[J]. Journal of Scientific Industrial Research, 2011, 70: 210-214.
[11]李明亮.基于模块化设计方法的城市轨道交通牵引计算软件研制[D].北京:北京交通大学,2008.
[12]于振宇,陈德旺.城轨列车制动模型及参数辨识[J].铁道学报,2011, 33(10):37-40.
[13]郜春海,陈德旺.基于模型选择和优化技术的自动驾驶制动模型辨识研究[J].铁道学报,2011, 33(10):57-60.
[14]P. Auer, N. Cesa-Bianchi, C. Gentile. Adaptive and Self-Confident On-Line Learning Algorithms[J]. Journal of Computer and System Sciences, 2002, 64(1): 48-75.
