数控机床主轴热误差建模参数优化*

赵昌龙，关雪松

(1.长春大学机械与车辆工程学院，长春 130022;2.吉林大学机械科学工程学院，长春 130022）

0 引言

近年来，随着制造业的迅猛发展，人们对数控机床加工质量的要求也不断提高，那么如何提高数控机床的加工质量则成为人们着重考虑的问题，而影响其加工质量的多种因素中，机床整体的热误差特别是主轴系统的热误差是最为重要的因素，而且利用热误差的补偿来提高加工质量相比传统的机床结构上的改进成本更低廉，因此有着十分显著的经济效益［1-6］。

在对数控机床热误差进行补偿的过程中，最为重要的就是建立精确的热误差补偿模型。目前，针对热误差建模的方法也很多，但传统的方法很难保证建模精度，而利用最小二乘支持向量机［7-8］的方法建立模型不但过程简单，而且对于计算速度很快，建模精度更高，本文正是在利用最小二乘支持向量机建立主轴热误差预测模型的过程中，运用matlab为平台在尽可能大的参数范围内，确定出模型所采用核函数的最优参数，以提高后期模型的预测精度。

1 主轴温度场与热误差采集

本文实验所用机床为FIDIA D165型高速铣削数控加工中心，整个实验过程里将型号为DS18B20的智能温度传感器分别置于主轴后轴承、前轴承以及距离主轴前轴承3/7轴长处［9］，共安置三个，对主轴的温度场变化情况进行实时采集，主轴热误差则通过固定在机床工作台上的NS-1D型位移传感器对Z方向上的热误差进行测量。温度传感器的布局情况以及温度采集软件界面如图1与图2所示。

图1 温度传感器布局实物图

图2 采集软件界面

采集系统可以按照实验人员的要求设计采样周期，本文将采样周期定为5分钟，实验所得数据如图3所示。

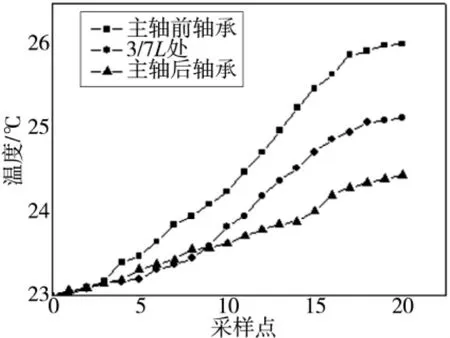
图3 温度场变化曲线

2 热误差模型参数优化方法

在利用LS-SVM进行建模的具体过程中，首先要确定建模时所用核函数，考虑到热误差模型输入数据的线性不可分性，文中采用了RBF型的高斯核函数，此类函数在处理问题的过程中具有灵敏性强且参数较少的优点。

在RBF核函数中只需确定两个待定参数，分别是敏感度参数σ和惩罚参数γ。其中，σ的选取结果决定了整个LS-SVM训练模型对所输入样本数据的敏感程度，若参数σ的选取值过大会造成预测模型反应相对迟钝，不能随着输入数据的快速变化而瞬时变化，而且收敛的速度比较相对，在这种情况下获得的预测模型在预测热误差的结果时会逼近一个值，造成模型精度的下降，反之，则过于灵敏，使外界干扰对模型的影响被放大。惩罚参数γ的选取情况则会直接影响预测模型的分类精度以及测试精度。因此，如何有效地确定建模参数σ和γ对于整个预测模型的建立过程来说有着十分重要的意义。

本文利用网格搜索法可以在一个较大的范围内对建模参数对(σ、γ）的组合选取进行优化，以提高最终的建模精度。

2.1 网格搜索法

网格搜索法［10］也可以称为穷举法，其优点在于能够在一个尽可能广泛的空间之内对待定参数或参数对的进行优化取值，对于处理一些非线性的问题具有很好的效果。其核心思想在于:在处理一个参数或者参数对的优化过程中，首先在一个大的区间内分化网格，进而在每个细化网格的有效节点上计算出目标函数的最终函数值，之后对函数值进行比较，最后根据模型的具体要求得到最优函数值所对应的有效节点，则此节点的对应值即为最优参数。本文的参数优化过程中只有一对待定参数(σ、γ），因此具有计算量小计算简单，运行效率高的优点。

2.2 参数优化过程

在利用网格法对待定参数对(σ、γ）进行优化之处，首先要以数控机床主轴温度场实时数据为X，以主轴在Z方向上的热误差数据值为Y，并将两组数据导入到模型中以进行后续分析，具体步骤如下:

(1）将实验中实际测得数据组X(温度值）和Y(热误差值）整理并导入到模型中;

(2）确定模型在优化训练过程中具体网格的数目;

(3）给定待优化参数对(γ，σ2）的初始值，并在尽可能的范围内进一步确定搜索所需起始点和范围等相关条件;

(4）对每个网格上的相应节点进行误差计算;

(5）利用matlab依据每个节点的计算结果得到预测误差曲面图形，待定参数对(γ，σ2）优化结果(X，Y）即为绘得误差曲面图形最低节点相对应的节点坐标值;

(6）为了得到最优结果，保证参数优化效果，本文进行了第二次的迭代处理;

(7）在第一次优化结果附近，利用更精细的网格划分再次利用网格搜索法进行优化处理，即重复步骤(1）至步骤(5）;

(8）经过第二次优化处理后获得的最优节点对应的坐标值，即为待定参数对(γ，σ2）的最优值，并给出这组最优参数(γ，σ2）的计算误差。

3 参数优化结果

经过两次迭代优化之后，在更大更精确的空间内获得的待定参数对(γ，σ2）的最优结果，即 γ=891.444，σ2=3.031，最优参数对训练模型预测的平均误差可以控制在.7%附近，预测精度理想。绘制优化结果的曲面图形如图4与图5所示。

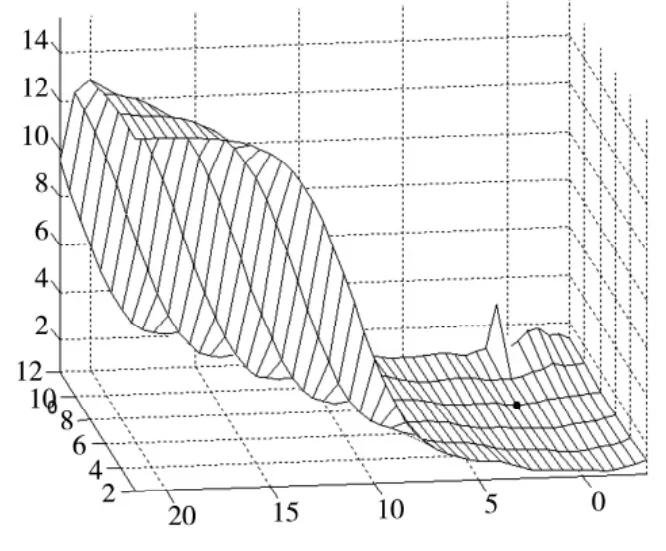
图4 第一次网格法优化结果

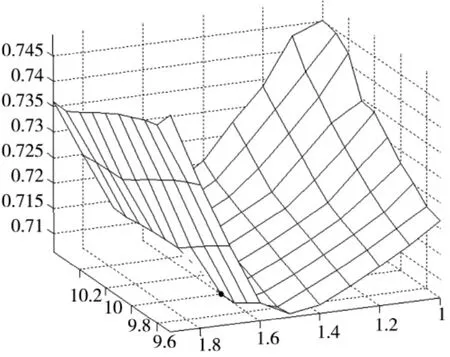
图5 第二次网格法优化结果

在得到了参数对的优化结果后，利用最小二乘支持向量机法对数控机床主轴的热误差进行建模，在建模过程中先后选取了两组不同参数，分别是(γ=1，σ2=1）和(γ =891.444，σ2=3.031），以验证参数优化后的建模效果，具体建模结果见图6与图7。将选用不同参数对的建模效果进行对比，可以清晰明确的看到，利用优化后的参数对进行建模，其效果更好，预测精度更高，证明了参数优化提高了整个模型的精度。

图6 参数取(γ=1，σ2=1）时建模结果

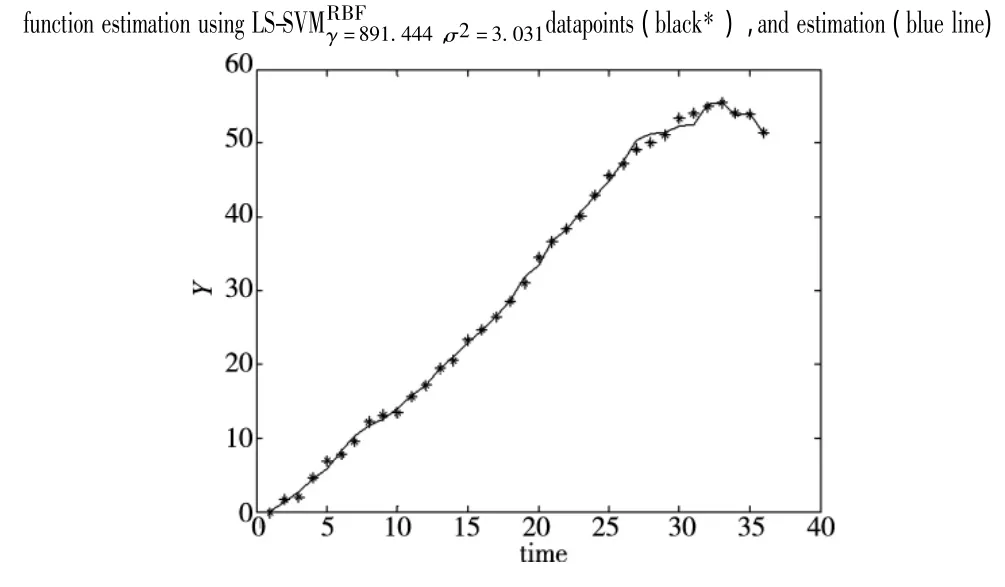
图7 参数取(γ=891.444，σ2=3.031）时建模结果

4 总结

本文针对利用LS-SVM建立数控机床主轴热误差预测模型过程中核函数参数对的优化问题，以matlab为平台，通过网格搜索法的两次优化迭代，在更为广阔的区间内，对待定参数对(γ，σ2）的取值进行了有效的优化，且计算简单，建模结果证明当参数对选为(γ=891.444，σ2=3.031）时，其建模效果良好。

［1］Chana R.，Manukid P.Geometric and force error compensation in a 3-axis-CNC milling machine［J］.International journal of machine tools and manufacture，2004，44:1283-1291.

［2］W.Gao，et al.Measurement and compensation of error motions of a diamond turning machine［J］.Precision Engineer，2007，31(3）:310-316.

［3］Xu Min，Jiang Shuyun，Cai Ying.An improved thermal model for machine tool bearings ［J］.International Journal of Machine Tools＆ Manufacture，2007，47:53-62.

［4］H.J.Pahk，S.W.Lee.Thermal error measurement and real time compensation system for the CNC machine tools incorporating the spindle thermal error and the feed axis thermal error［J］.Int J Adv Manuf Technol，2002，20:487-494.

［5］张宏韬，冯同建，曹洪涛，等.高速机床的关键技术和发展趋势［J］. 机械制造，2009，44(3）:12-14.

［6］刘焕牢.数控机床几何误差测量及误差补偿技术的研究［D］.武汉:华中科技大学，2005.

［7］郭新辰.最小二乘支持向量机算法的应用研究［D］.长春:吉林大学，2008.

［8］Friddrichs F，Igel C.Evolutionary tuning of multiple SVM parameters［J］.Neurocomputing，2005，64(C）:107-117.

［9］Zhao Changlong，Wang Yiqiang.Optimization of measuring points based on the grey system theory for spindle of CNC machine tool.2009 IEEE InternationalConferenceon Mechatronics and Automation，ICMA 2009，686-690.

［10］许亚洲.基于最小二乘支持向量机的数控机床热误差建模的研究［D］.浙江大学，2006.