第二类吸收式热泵PID控制算法研究
2013-11-23王睿宇武晓伟方书起
王睿宇,武晓伟,方书起
(1.郑州大学 化工与能源学院,河南 郑州 450001;2.东方电气股份有限公司 国际工程分公司,四川 成都 610036)
第二类吸收式热泵系统依靠输入废热运行,无三废排放,是一种高效节能设备。正常工况下,各循环流量基本保持稳定,此时控制各设备的液位稳定,输出端即能保持稳定。第二类吸收式热泵的自动控制系统需要快速调节各设备液位并保持稳定状态。由于废热来自上游工艺流程,受到诸多干扰因素的影响,因此无法建立准确的数学模型。液位的调整属于连续过程,适用位置型PID调节方式[1]。
1 标准PID调节
1.1 PID调节各部分作用
PID调节全称是比例积分微分调节,是对被调量与给定值的偏差分别进行比例(proportion)、积分(in-tegral)和微分(differentiation)运算,构成连续信号以控制执行器的模拟调节。
比例调节作用:是按比例反映系统的偏差,系统一旦出现了偏差,比例调节立即产生调节作用以减少偏差。比例作用大,可以加快调节,但是过大的比例会使系统的稳定性下降,甚至造成系统的不稳定。
积分调节作用:是使系统消除稳态误差,提高无差度。因为有偏差,积分调节就进行,直至无偏差,积分调节停止,积分调节输出常值。积分作用的强弱取决于积分时间常数TI,TI越小,积分作用就越强。加入积分调节可使系统稳定性下降,动态响应变慢。积分作用常与另2种调节规律结合,组成PI调节器或PID调节器。
微分调节作用:微分作用反映系统偏差信号的变化率,具有预见性,能预见偏差变化的趋势,因此能产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除。因此,可以改善系统的动态性能。在微分时间选择合适情况下,可以减少超调,减少调节时间。微分作用对噪声干扰有放大作用,因此过强的微分调节对系统抗干扰不利。此外,微分反映的是变化率,当输入没有变化时,微分作用输出为零。微分作用不能单独使用,需要与另外2种调节规律相结合,组成PD 或 PID 控制器[2]。
1.2 标准位置型PID调节
标准位置型PID控制方程分为模拟形式和离散形式[3-4],如表1所示。

表1 标准位置型PID表达式
自动控制系统中的控制程序并非连续的模拟方式而是离散的控制点,所以采用标准位置型PID表达式的离散形式。离散型的表达式为

式中,KP为比例系数,TI为积分时间常数,TD为微分时间常数。
1.3 标准位置型PID数值模拟
计算机数值模拟采用 VC++语言编程[5-6],模拟调整值与PID位置输出值呈线性关系。由于控制点为离散点,输出值为连续曲线,所以采用了插值算法[7-8]。数值模拟曲线如图1所示。

图1 标准位置型PID调整曲线
1.4 PID调节核心代码(PIDCalc函数)


2 标准位置型PID调节的改进
2.1 改进方案
标准PID调节中增大比例系数KP可以加快调节,减少误差,但是过大的比例系数会导致系统的不稳定。经过计算机数值模拟程序,比例系数KP过大造成系统不稳定的典型表现如图2所示。为了加快PID调节速度,所以对标准PID的比例环节进行修改。
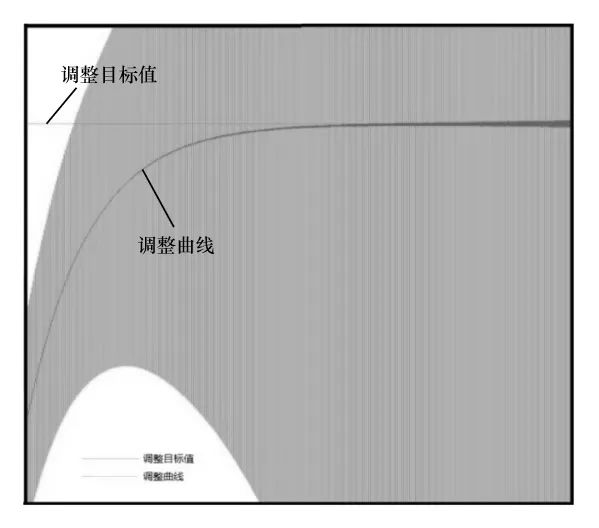
图2 KP过大造成调节不稳定
为了避免比例系数KP过大而造成系统的不稳定,自动控制系统中引入一个新变量DE来衡量系统偏差大小。此变量可由自动控制系统超级管理员设定,默认值为10%。在改进型的PID调节中,比例系数KP不再是一个固定值,而是根据系统当前值与设定值的差值(Δu)大小来确定比例系数KP。Δu为非负数,当Δu大于设定值DE时,系统使用一个较大的比例系数,以加快系统调节的速度;当Δu小于或等于设定值DE时,系统使用一个较小的比例系数,以避免系统出现不稳定的情况。在改进型PID中,比例系数KP不是一个常系数,而是由独立算法产生,算法程序结构如图3所示。
改进后的位置型PID控制方程为


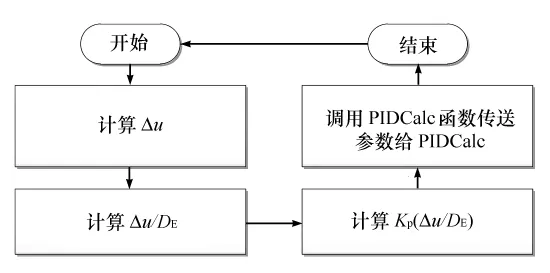
图3 比例系数算法结构
2.2 问题分析与处理
通过数值模拟发现,在改进型位置PID调节中,如果设定值与当前值相差太大,仍然可能导致控制系统出现不稳定的情况[9-10]。这是因为控制点为离散点,对系统的控制并不连续。数值模拟中不稳定情况如图4所示。

图4 改进型位置PID调节不稳定
鉴于以上不稳定情况,需要对比例系数进行限制,取稳定段的最大值。这样可以有效避免出现振荡而不稳定的情况。同时,在实验中还发现,由于比例系数变化大,可能造成电动调节阀处于全开或全闭情况。全开情况允许出现,而全闭情况是不允许出现的,因为全闭时循环回路处于断开状态,同时会影响到系统中其他电动调节阀的控制。所以在程序设计时需要对电动调节阀最低开启程度作出相应的限制。对于比例系数最大值的确定除了计算机数值模拟的方法外,还同时采用了以下试验性方法。
确定比例系数KP时,首先去掉PID的积分项和微分项,一般是令TI=0、TD=0,PID为纯比例调节。输入设定为系统允许的最大值,由0逐渐加大比例系数KP,直至系统出现振荡;再反过来,从此时的比例系数KP逐渐减小,直至系统振荡消失,记录此时的比例系数KP,此时比例系数KP即为比例系数稳定段的最大值[11]。
2.3 改进后位置型PID调节
通过计算机数值模拟,限定比例系数的改进型PID调节效果如图5所示。

图5 改进后PID调节数值模拟效果
3 改进位置型PID调节实验测试
进行在线测试之前,对时产500kg蒸汽的第二类吸收式热泵系统进行了改造:在设备上连接温度、液位、真空度传感器,将关键控制阀门由手动阀门更换为电动调节阀门。在测试中,将系统更改为手动模式,手动设定液位值,依靠改进型PID调节算法控制电动调节阀。通过手动调节液位设定值,可以让设备液位的当前值和设定值差值变大,从而检测改进型PID调节算法的调节能力。为了保证设备的安全,自动控制系统规定,设备液位的调整范围为10%~90%。实际测试效果如图6所示。
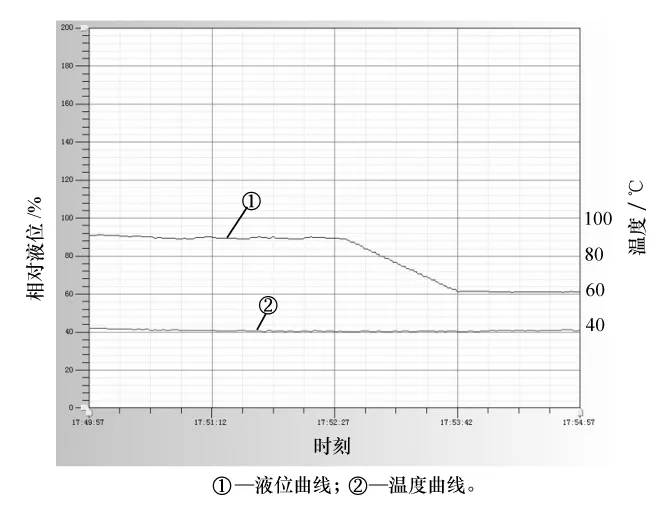
图6 实验测试曲线
从图6可以看出,测试中将液位从90%重设到60%,整个过程用时90s,设备液位即完成调节,并在60%液位处保持稳定。在改进型PID调节的整个过程中,始终保持很快的调节速度,没有超调,在完成调节的时刻即开始保持当前液位,没有来回振荡的微调过程。所以,改进型PID调节达到了预期的效果[12]。
实际测试图与数值模拟曲线有所不同的原因是:受到电动调节阀自身能力限制,曲线处于下降段时,电动调节阀已经达到最大开启位置,即改进位置型PID输出值受到硬件限制;而数值模拟的时候,并没有对PID调节的输出进行限制,数值模拟曲线是理想状态下的调整曲线。
4 结论
改进位置型PID调节算法相对于标准位置型PID调节算法,不仅加快了调节速度,还加强了调节的精确性。改进的控制算法达到了预期的控制效果,符合设计要求,完全能够满足第二类吸收式热泵的控制要求。
(References)
[1]张烨.大空间中央空调PID控制算法[J].南京师范大学学报:工程技术版,2007,7(2):37-40.
[2]王建辉,顾树生.自动控制原理[M].北京:清华大学出版社,2007.
[3]郭振凯,顾文锦.王海玲,等.基于离散非线性PID控制的十字梁实验系统研究[J].系统仿真学报,2003,15(9):1322-1324.
[4]周佩冬,欧林林,俞立,等.满足多性能指标的线性离散时滞系统PID控制器设计[C]//第29届中国控制会议论文集.2010:3554-3559.
[5]黄维通,马力妮.C语言程序设计[M].北京:清华大学出版社,2003.
[6]陈天华.面向对象程序设计与VISUAL C++6.0教程[M].北京:清华大学出版社,2006.
[7]徐艳,董江涛,王少华,等.基于模糊隶属度的图像空间距离修正插值算法[J].物理学报,2010,59(11):7535-7539.
[8]史凌峰,郭宝龙.一种感兴趣目标区域自动插值算法[J].西安电子科技大学报:自然科学版,2006,33(2):195-199,246.
[9]曹刚.PID控制器参数整定方法及其应用研究[D].杭州:浙江大学,2004.
[10]曹刚,俞海斌,徐巍华,等.大时滞不稳定对象的PID控制[J].仪器仪表学报,2005,26(3):301-303,324.
[11]王广雄,袁欣,何朕,等.不稳定对象的PID控制[J].控制与决策,2002,17(5):611-613.
[12]王鹤曾.工业过程PID控制器的设计与性能评价研究[D].杭州:浙江大学,2004.
