燃气发展规划中储气需求的计算
2013-11-21张悦张云莉刘学智
张悦 张云莉 刘学智
山东一通工程技术服务有限公司
天然气作为一种清洁能源已逐步成为城市燃气的主气源,在城市燃气发展中占有非常重要的地位。然而由于各类天然气用户用气量变化的不规律性,导致天然气的耗气量随月、日、时而变化,而气源供应又是相对稳定的,难以完全按照城市用气工况来供气,为了解决供需之间的矛盾,使用户稳定用气,需设置有效的调峰手段,使燃气输配系统供需平衡。解决城市各类用户时不均匀性,目前使用较多的为长输管道储气和LNG储配站储气。本文就燃气发展规划中储气设施储气量问题进行分析,满足城市发展过程中居民、商业及部分工业用户不间断供气。
1 储气量的确定
燃气发展规划中多使用高压管道储气和储气罐储气的方式,在用气高峰时,首先采用管道储气的方式,当管道储气无法保证各类用户不间断用气时,将储气罐中的液化天然气气化、调压、计量后与中压管网对接,实现向各类用户供气。在分析储气需求时,首先对长输管道储气量进行计算分析,再根据用气量需求,求出储气罐所需要的气量。
1.1 长输管道储气量
长输管线末端是指上游管线分输站至城市门站之间的管段,该管段不仅具有输气能力,还有一定的储气能力,因此充分利用输气管段末端的储气能力,可以减少储罐的数量和脱水工作量。
长输管线输气过程中受到各种扰动,如各类用户用气的不均匀性、间断性及相关设备的启停、外界环境变化对燃气轮机的影响等。这些扰动直接导致天然流量和压力沿输气管线随时间不断发生变化。由于扰动产生的作用在高压输气过程中表现得比较明显,这就决定了对天然气长输管线的输气过程应按照不稳定流来考虑[1]。
1.1.1数学模型的建立
长输管道中流体遵循一维不稳定流动,管道中主要以流速、压力、密度、温度等物理量反映气体流动状态,基于流体动力学理论,并考虑天然气在管段中流动时与土壤之间存在换热现象和焦耳-汤姆逊效应产生的温度变化,建立了如下长输管道动态数学模型[2]:

式中:p为管道中天然气的压力,Pa;x为沿管线的距离,m;ρ为天然气密度,kg/m3;v为管段中气体流动速度,m/s;t为时间,s;g0为重力加速度,m/s2;h 为管道的高程,m;λ为水力摩阻系数;D为管道内径,m;c为气体中的声速,m/s;Z为气体的压缩因子;R0为气体常数,J/(kg/K);T为气体温度,K;K为天然气到土壤的传热系数,W/(m2/K);T0为环境温度,K;cp为天然气的比定压热容,J/(kg/K);Dh为天然气的焦耳-汤姆逊系数。
边界条件:x=0,Q(0,t)=Q0;x=l,Q(l,t)=Q(t);x=0,P(0,t)≤Pmax;x=l,P(l,t)≥Pmin。
1.1.2计算求解
文献[3]提供了基于守恒原理的Wendroff差分格式,由该差分格式建立的方程组是一个大型的非线性方程组。为了减小求解难度,在求解之前根据管道实际运行工况,对数学模型进行以下适当的简化[4]。
1)在实际的输气管道中,天然气流速不会很大(接近声速),因此可以忽略对流项。
2)流量随时间的变化不会太大,可以忽略惯性项。
3)起点与终点的高差不超过200m时,可以忽略高差带来的影响。
于是式(1)可以简化为:

联立式(2)和式(5),可以得到式(6):

采用分离变量法对式(6)进行求解,假定
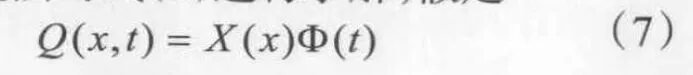
将式(7)代入式(6)得到

等号左边仅为t的函数,右边仅为x的函数,设等号左右两边同等于μ,即

结合边界条件求解得出

式(13)、(14)反映了长输管线中天然气流量、压力随时间、空间的变化情况。
1.1.3长输管道储气量的计算
由前面的分析、计算,可以计算出输气管线中流量、压力与末端流量变化之间的关系。因此,根据储气调峰原理,长输管线的储气量可以由下式计算得到:
管段末端储气量(单位m3)

式中:△Qm为管道的储气量,kg;ρ0为天然气在标准状态下的密度,kg/m3。

1.2 储气罐储气量的计算
储气罐储气能在停电、上游管道出现问题、制气或输配设备发生暂时故障时保证一定程度的供气。因此,确定储气罐的实际容积,应考虑到供气的波动、用气负荷的误差、气温等外界条件的突然变化以及储气设备的安全操作要求,储气罐的实际容积应有一定的富裕。具体计算根据以下两式进行计算。
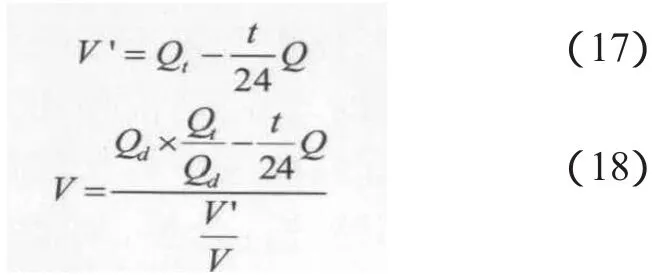
式中:V'为所需的储气容积,m3;V为储气罐的容积;m3;Qt为 t小时中的用气量,m3;Qd为最大日用气量,m3;Q为制气能力,m3;t为一日中小时用气量大于制气能力的小时数,h。
2 实例计算
表1为某长输管道储气不稳定流实测数据[5]。按负荷曲线,储气从晚21时开始,晨7时结束。管道需保证入口流量为 56000m3/h(P0=0.101325MPa,T0=293K),储气前,管道始端压力为4.66MPa,未端压力为1.42 MPa,管内温度10℃,管内径30cm,管长132km。储气量 ΣQi=222.2×103m3。
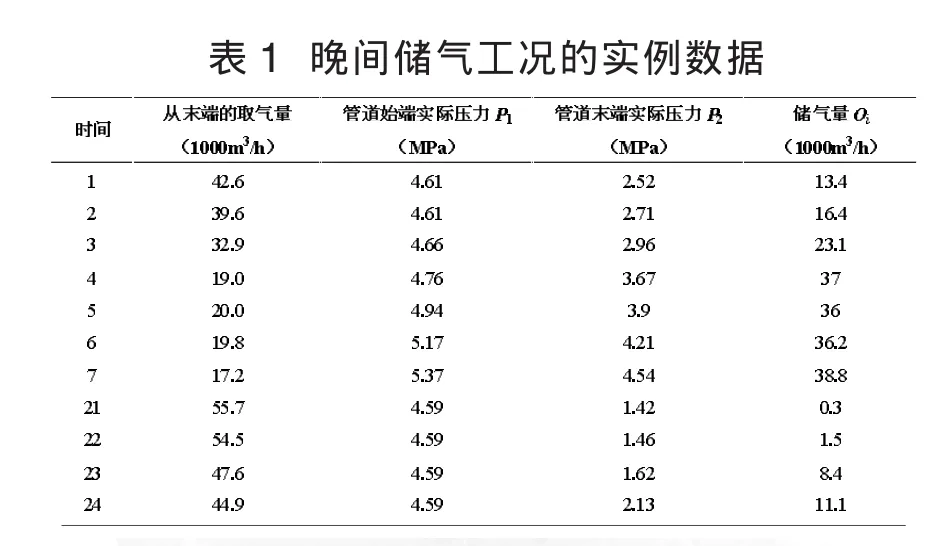
表1晚间储气工况的实例数据

图1 管道储气计算值与实例数据对比
根据以上计算式,结合表1数据,求得管道、储气罐储气计算值,并将管道储气计算值与实例数据对比见图1。从图1可见,管道计算值与实例数据误差在10%左右,计算公式可以利用;储气罐储气量与长输管道储气量的比值最大为8.77%,最小为-60.4%。
3 结论
1)燃气发展规划中采用的储气方式大多为两种,一种是长输管道天然气储气,一种是液化天然气储配站储气。储气罐储气量与长输管道储气量的比值最大为8.77%,最小为-60.4%。
2)利用一维非稳态计算公式,推导了长输天然气管道储气量的计算公式,并通过实例验证,结果表明计算结果与实例数据的误差在10%左右。
[1] 隋元春,薛世达.沿途有分输的长输燃气管道不稳定计算[J].煤气与热力,1988,(4):25-27
[2] 唐建峰,段常贵.燃气长输管道动态模拟及末端储气研究[J].油气储运,2000,(7):24-27
[3] 李长俊,曾自强.天然气在管道系统中不稳定流动的分析[J].天然气工业,1992,(4):69-71
[4] 段常贵,杨立民.燃气长输管线分析与末段储气计算[J].煤气与热力,1997,(3):16-20
[5] 李猷嘉.长输管道末段储气量的计算与分析[J].煤气与热力,2002,22(1):8-11
