基于逻辑回归的重庆地区降雨型滑坡预报模型

唐红梅，魏 来，高阳华，唐云辉

(1.重庆交通大学岩土工程研究所，重庆 400074;2.重庆市气象科学研究所，重庆 401147)

0 引言

在热带和亚热带地区，存在大量残积土和膨胀土边坡，在雨季时短历时强降雨往往会引发该地区大量浅层滑坡破坏［1-3］。重庆地区处于亚热带，降雨充沛且不均匀，加上特殊的地质地貌水文条件，该地区长久以来一直是降雨型滑坡的高发地之一。

降雨诱发滑坡一直是学术界研究的热点和难点，其研究目前主要有两种思路，一是基于降雨诱发滑坡事件的统计分析，获得降雨诱发滑坡的相关性规律［4-6］，继而得到经验性降雨阈值模型;另一种是基于降雨入渗机理分析，构建边坡降雨入渗稳定性模型，通过模型试验或数值模拟等手段探讨滑坡发生的内在破坏机理［7-10］。由于降雨诱发滑坡研究的复杂性，统计分析仍然是研究降雨诱发滑坡灾害的主要手段。最近几年有学者将逻辑回归统计方法运用到降雨诱发滑坡阈值模型的推导［11-13］以及滑坡敏感性区划中［14-16］，并且都取得了不错的效果。

本文采用Logistic回归方法，通过整理大量降雨诱发滑坡资料，结合以往研究中没有考虑的当日最大小时降雨这一降雨因子进行综合分析，推导出重庆地区降雨型滑坡的预报模型，并用降雨型滑坡实例检验该模型。本文成果可作为重庆地区降雨型滑坡灾害预测预报研究工作的参考。

1 逻辑回归模型

Logistic回归模型是一个结合了统计模型和确定性模型的完整模型［15］。在多元回归分析中，常常要求因变量是连续变量，而降雨诱发滑坡却是不连续的二元变量，降雨诱发因子可以作为自变量。若采用普通多元回归方法来分析，会违反一些重要假设［17］，导致回归估计产生严重误差，以致无法进行合理的假设检验。鉴于此，采用逻辑回归分析中的 Binary Logistic回归模型，探讨在特定降雨条件下滑坡的发生概率。

假设在降雨自变量影响下，发生滑坡时的概率为1，不发生滑坡时的概率为0。p为预测滑坡发生概率，取值范围为［0，1］，则(1-p)即为预测不发生滑坡的概率。p/(1-p)为滑坡Logistic回归发生比，对其取自然对数 lnp/(1-p)］。自变量为 x1，x2，…，xk，因变量为p，则Logistic线性回归函数可表示为:

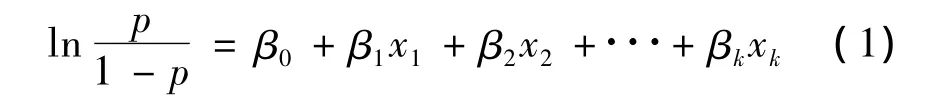
式中:βi(i=0，1，2，…，k)为回归系数。

根据式(1)，可得:

利用式(2)便可以预测降雨条件下滑坡灾害发生概率，其难点是降雨诱发滑坡数据、降雨因子的筛选和Logistic回归方程的拟合。

2 数据收集与处理

为了能够得到尽量准确的滑坡降雨资料，本文主要选取重庆市地质环境监测总站提供的2003～2006年发生的近千个滑坡资料，筛选出具有确切发生时间、发生地点的滑坡个例，结合重庆市气象局提供的距离相关滑坡最近的气象站观测的2003～2006年小时降雨资料研究滑坡致滑概率。为了减少人为因素对滑坡数据的干扰，本文选择相邻区域96h内至少发生2次的滑坡点数据，最终筛选出284例降雨诱发滑坡事件。经统计，所得到得284例滑坡事件有95%为中浅层(厚度＜20m)滑坡。

由于降雨诱发滑坡的统计数据只能精确到日，假设某日0h～24h之内发生滑坡，降雨量数据也取同时段内数据，则当日是一次p=1的降雨诱发滑坡事件，所遴选的284例降雨滑坡事件可以整理成51例p=1的滑坡事件。为了建立逻辑回归模型，还需要在这51例已发生滑坡事件相邻日期加以遴选，得到51个未发生滑坡(p=0)的降雨事件。

在降雨因子的选取上，结合国内外降雨诱发滑坡研究情况以及重庆地区实际条件，降雨因子除当日降雨(P0)外，还考虑滑坡发生前第1日(P1)、第2日(P2)、…、第6日(P6)降雨数据。为了研究当日降雨中短时强降雨对滑坡激发的影响，且重庆市气象局自2003年以来进行降雨量的逐小时监测，客观条件已经达到，因此考虑当日降雨中的最大小时降雨(Ph)(表1)。

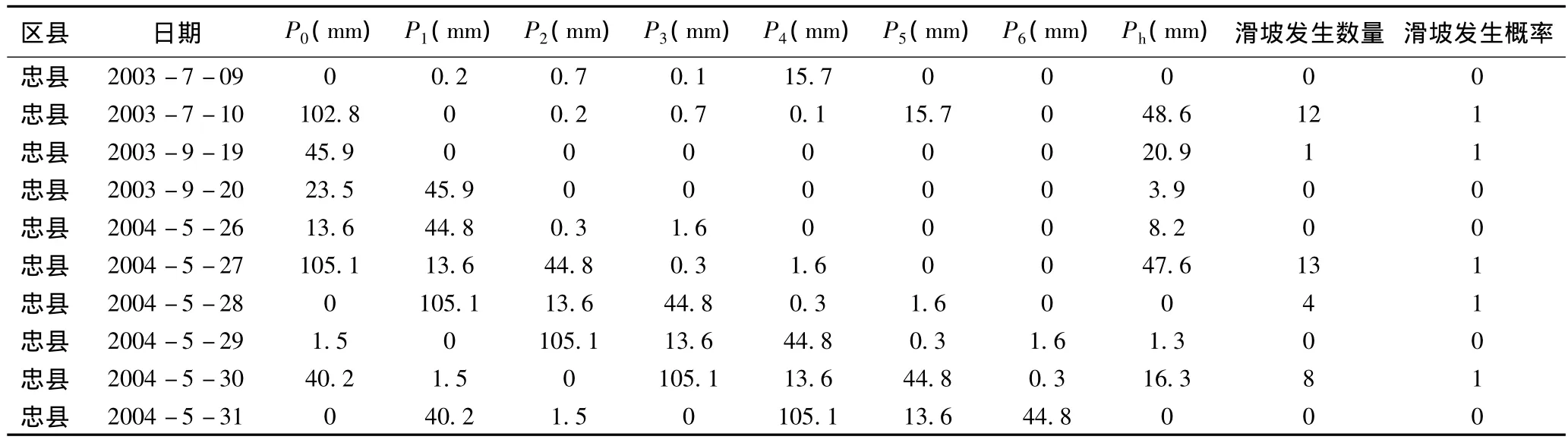
表1 重庆部分地区降雨诱发滑坡数据Table 1 Rainfall-induced landslide date in part of Chongqing area

3 结果分析

将前述降雨资料输入SPSS13.0软件处理，获得Logistic回归方程中的相关统计量(表2)。

由表2可知，当日降雨量(P0)回归系数最大，对诱发滑坡的作用最显著，距滑坡发生日数越久，其回归系数有下降趋势。滑坡发生前第4日(P4)的回归系数为0.01，其影响已经可以忽略不计。

wald检验值可以进一步说明不同降雨因子对诱发滑坡的影响，wald检验相当于简单线性回归分析中的t检验，其检验统计量渐进服从χ2分布。对照自由度为1的χ2分布进行检验，当错误概率为5%时，χ2分布值为3.84。表2中wald检验值大于3.84的表示拒绝变量不显著的假设，表明变量P0、P1、P2相对于滑坡发生具有显著影响。这个结果表明，对于重庆地区中浅层滑坡，滑坡发生的当日降雨以及前2d降雨对其影响最大，滑坡发生前2d以上降雨对其影响已经很微小。

表2 Logistic回归方程相关统计量Table 2 Related statistics of logistic regression equation

进行回归分析时，剔除对模型结果不显著的变量，可以使模型更加准确。剔除对诱发滑坡的几个不显著降雨变量 P3、P4、P5、P6和 Ph，重新进行 Logistic回归分析。

考虑到本文所选重庆地区降雨型滑坡资料主要为中浅层滑坡，现实中短时强降雨诱发中浅层滑坡主要为有两种破坏方式，一是强降雨使表层土体迅速饱和，强降雨的激发使得土体产生流滑破坏;另一种是当滑坡体上有裂缝时，入渗系数会变得很大，并且短时强降雨使裂缝迅速充水，产生静水压力，进一步加速了滑坡的产生。因此有必要验证当日最大小时降雨量Ph对预测模型的影响。

验证Logistic回归模型模型效果的一个很重要的手段是评价模型预测分类结果。将概率P=0.5作为预测模型滑坡发生与否的临界值点，然后把降雨自变量数据代入预测模型，所的预测值大于0.5便认为在当前降雨组合条件下将会发生滑坡，小于0.5则认为不发生。然后再跟样本中实际发生滑坡与否的数据作比较，得到模型预测分类表(表3)。

经过检验，当降雨因子组合为P0、P1、P2时，模型的总判对概率为86.3%，而当降雨因子组合为P0、P1、P2、Ph时，模型的总判对概率为 87.3%(表 3)，因此，最终模型采用P0、P1、P2、Ph的降雨因子组合。表3中实际发生滑坡的51个降雨组合通过预测模型判断成功了45个，失败了6个，判对率是88.2%;未发生滑坡的判对率是86.3%，模型总判对率为87.3%。考虑到降雨滑坡数据采用自重庆6个区县市，地区跨度大，地质气象等客观因素迥异，因此预测模型的预测判对概率是相对满意的。

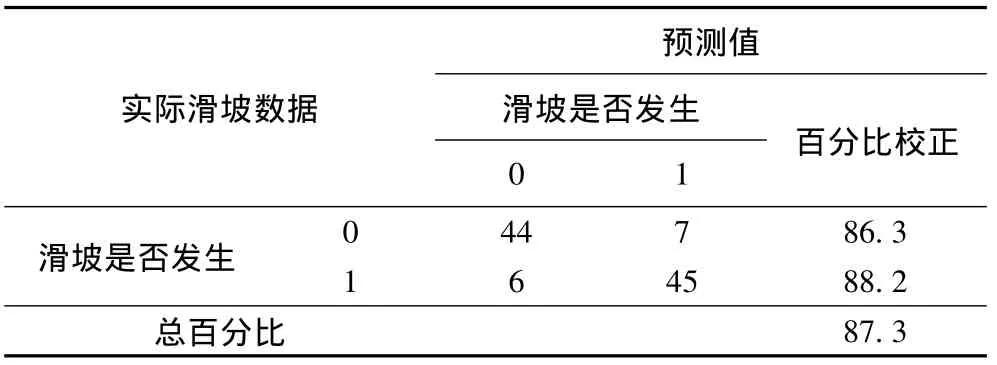
表3 模型预测分类表(a)Table 3 The classification of model prediction(a)

通过对降雨因子 P0、P1、P2、Ph进行最终 Logistic回归分析，得到最终相关统计量(表4)。将表中的回归系数以及常数项数据带入到式(2)，得到基于Logistic回归的重庆地区降雨预测模型:

式中:

P——预测滑坡发生概率;

P0——当日降雨量;

Pi(i=1，2)——据滑坡发生前第 1，2 天的降雨量;

Ph——滑坡当日最大小时降雨量。

表4 最终Logistic回归方程相关统计量Table 4 Related statistics of ultimate logistic regression equation

当日降雨量P0与当日最大小时降雨Ph之间的相关系数为0.814，正如一般线性回归一样，如果某自变量与另自变量之间有较强的线性关系，那么在Logistic回归中会出现多重共线性问题，Logistic回归系数的标准误将过度增加，检验效能降低。为了检验该预测模型整体的拟合效果，SPSS软件分别给出了3种评价指标(表5)。其中-2倍对数似然值类似于经典回归分析中的离差平方和，近似服从自由度为(K-J-1)的χ2分布，K表示样本个数，J表示参数个数［17-18］。上述模型中 K=102、J=5，当显著性水平为5%时，自由度96的χ2分布值为119.85，远大于表4中的对应值61.56，不可拒绝模型完美拟合的假设，说明该逻辑回归模型整体拟合效果良好。表5中Cox＆Snell R方以及Nagelkerke R方统计量体现了回归模型所能解释的因变量变异的百分比，当Cox＆Snell R方值大于0.4，Nagelkerke R方值大于0.5时，便认为模型整体有效性良好［18］。本模型中Cox＆Snell R方值为0.543，大于0.4;Nagelkerke R方值为0.724，大于0.5。

在所统计的284例降雨诱发滑坡事件中，有68例滑坡无前期降雨或者前期降雨总量小于10mm，因此有必要专门研究重庆地区短时强降雨诱发滑坡降雨量阈值，即无前期降雨时诱发滑坡的当日降雨量与当日最大小时降雨量之间的关系(图1)。

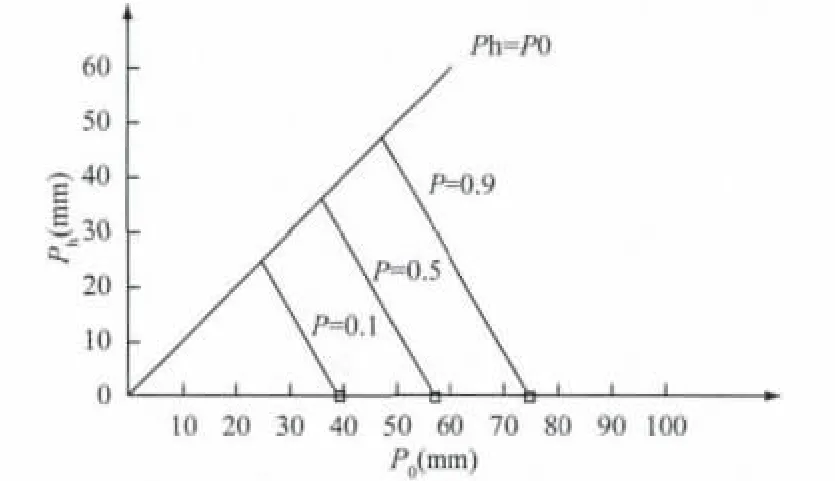
图1 无前期降雨时不同滑坡概率下当日降雨量与当日最大小时降雨之间的关系Fig.1 The relationship between daily rainfall and daily maximum hourly rainfall under different probabilityin the case of no antecedent rainfall

无前期降雨情况下(P1=P2=0)达到一定滑坡发生概率值，随着当日降雨量P0降低，所需最大小时降雨量Ph随之增大，这可以理解为若当日降雨量较少时，诱发滑坡则需要更大的短时激发降雨强度，现实中这类滑坡多为浅层流滑破坏;当无前期降雨且当日只降1h雨(P0=Ph)，诱发滑坡概率值P=0.5，代表降雨诱发滑坡的临界状态，代入可得P0=Ph=34.6mm，即诱发滑坡的临界小时降雨强度为34.6mm;同理P=0.1时，P0=Ph=23.2mm;P=0.9时，P0=Ph=46mm(图1)。另外一种情况是随着当日最大小时降雨量Ph的降低，即当日雨型比较平均时，诱发滑坡所需的日降雨量P0会增大。如图1所示，Ph趋近于0时，P0在滑坡发生概率P=0.1，P=0.5，P=0.9 下分别约等于38mm，56.6mm，75mm。

4 实例检验

为了验证所得(3)式的实用性和预报准确性，选取2007～2009年忠县诱发23例滑坡的7次降雨事件以及未发生滑坡的3次降雨事件加以验证。为了排除人为等非降雨因素影响，本次选取仍然采用相邻区域一次降雨诱发的滑坡不少于2次。将各降雨因子分别代入(3)式，结果见表6。

由表6可见，当降雨因子数据代入(3)式，并且以概率值0.5作为滑坡发生与否的临界值。预测模型的准确率能够达到90%，和之前用SPSS软件预测的滑坡判对率较为接近。预测失败的4例滑坡发生在2008年8月30日，观察其降雨数据发现当日降雨为3.6mm，当日最大小时降雨为1.6mm，但是前2d降雨很大，达到110.8mm。大量本地区降雨诱发滑坡文献资料表明，此降雨因子足以诱发滑坡。分析其原因，可能是由于雨量监测点距离滑坡事发地点较远，且发生滑坡灾害的地点一般海拔较高，实际降雨量与监测值有一定差距;亦或发生滑坡地点较为偏僻，未被及时发现。

表6 忠县滑坡降雨因子及滑坡预测值Table 6 Landslide rainfall factors and landslide prediction in Zhongxian

由此可见(3)式具有一定的准确性和实用性，但是需要通过进一步的模型试验或实际降雨诱发滑坡资料加以检验修正。

5 结论

降雨诱发滑坡一直是学术界研究的热点和难点，本文整理了近几年重庆地区降雨型滑坡大量数据，运用Logistic回归方法，通过 SPSS软件得到了基于Logistic回归的重庆地区降雨型滑坡预测模型。并运用SPSS软件以及滑坡实例分别验证该模型，其判对概率都超过85%，结果相对较为满意，模型可做重庆地区降雨型滑坡的定量化预测。

通过Logistic回归相关统计量筛选出了对滑坡较为显著的降雨因子组合，当降雨因子组合为P0、P1、P2、Ph时，模型的总判对概率为87.3%。并且重点讨论了无前期降雨情况下的当日降雨量与当日最大小时降雨之间的关系，得到了不同滑坡发生概率下的降雨阈值曲线，结果可作为预测该降雨型滑坡的参考值。

由于客观因素的限制，例如有些雨量站距离滑坡较远，未使用降雨插值方法，一些统计降雨量数据并不准确;或者有关县市具有准确发生日期的滑坡资料的缺乏，造成所选重庆地区降雨滑坡事件的不均匀性;再者本文所选择降雨诱发滑坡资料多为重庆地区中浅层滑坡，这都会令所得滑坡预测模型在应用上具有一定的局限性及偏差，需要进一步通过滑坡实例或滑坡模型试验加以修正。

［1］吴长富，朱向荣，尹小涛，等.强降雨条件下土质边坡瞬态稳定性分析［J］.岩土力学，2008，29(2):386-391.WU Changfu，ZHU Xiangrong，YIN Xiaotao，et al.Analysis of soil slope’s transient stability under intensive rainfall［J］.Rock and Soil Mechanics，2008，29(2):386-391.

［2］陈伟，莫海鸿，陈乐求.非饱和土边坡降雨入渗过程及最大入渗深度研究［J］.冶矿工程，2009，29(6):13-21.CHEN Wei，MOU Haihong，CHEN LeQiu.Study on Rainfall Infiltration Process and the Biggest Infiltration Depth for Unsaturated Soil Slope［J］.Mining and Metallurgical Engineering，2009，29(6):13-21.

［3］陈善雄，谭新，柳治国.降雨条件下土质边坡稳定性预测预报方法［J］.岩土力学，2002，23:31-36.CHEN Shanxiong，TAN Xin，LIU Zhiguo.A prediction method of slope stability due to permeation of rainwater［J］.Rock and Soil Mechanics，2002，23:31-36.

［4］Guzztti F，Peruccacci S，Rossi M，et al.Rainfall thresholds for the initiation of landslides［J］.Meteorology and Atmospheric Physics，2007，98(3-4):239-267.

［5］麻土华，李长江，孙乐玲，等.浙江地区引发滑坡的降雨强度-历时关系［J］.中国地质灾害与防治学报，2011，22(2):20-25.MA Tuhua，LI Changjiang，SUN Leling，et al.Rainfall intensity-duration thresholds for landslides in Zhejiang region，China［J］.The Chinese Journal of Geological Hazard and Control，2011，22(2):20-25.

［6］李媛.四川雅安市雨城区降雨诱发滑坡临界值初步研究［J］.水文地质工程地质，2005(1):26-29.LI Yuan.Preliminary study on precipitation threshold of precipitation induced landslides in Ya’an Yucheng District，Sichuan Province［J］.HYDROGEOLOGY AND ENGINEERING GEOLOGY，2005(1):26-29.

［7］吴宏伟，陈守义，庞宇威.雨水入渗对非饱和土坡稳定性影响的参数研究［J］.岩土力学，1999，20(1):1-14.WU Hongwei，CHEN Shouyi，PANG Yuwei.Parametric Study of Effects of Rain Infiltration on Unsaturated Slopes［J］.Rock and Soil Mechanics，1999，20(1):1-14.

［8］Crosta G B，Frattini P.Distrtbuted modelling of shallow landslides triggered by intense rainfall［J］.Nat Hazard Earth Sys Sci，2003，3(1-2):81-93.

［9］刘礼领，殷坤龙.暴雨型滑坡降水入渗机理分析［J］.岩土力学，2008，29(4):1061-1066.LIU Liling，YIN Kunlong.Analysis of rainfall infiltration mechanism of rainstorm landslide［J］.Rock and Soil Mechanics，2008，29(4):1061-1066.

［10］李焕强，孙红月，孙新民，等.降雨入渗对边坡性状影响的模型实验研究［J］.岩土工程学报，2009，31(4):589-594.LI Huanqiang，SUN Hongyue，SUN Xinmin，et al.Influence of rainfall infiltration on slopes by physical modeltest［J］.Chinese JournalofGeotechnical Engineering，2009，31(4):589-594.

［11］Glade T，Crozier，M J，Smith P.Applying probability determination to refine landslide-triggering rainfall thresholds using an Empirical“Antecedent Daily Rainfall Model”［J］.Pure and Applied Geophysics，2000，157:1059-1079.

［12］丛威青，潘懋，李铁锋，等.降雨型泥石流临界雨量定量分析［J］.岩石力学与工程学报，2006，25(1):2808-2812.CONG Weiqing， PAN Mao， LITiefeng， etal.Quantitative analysis of critical rainfall-triggered debris flows［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(1):2808-2812.

［13］李铁锋，丛威青.基于Logistic回归及前期有效雨量的降雨诱发型滑坡预测方法［J］.中国地质灾害与防治学报，2006，17(1):33-35.LI Tiefeng，CONG Weiqing.A method for rainfall-induced landslides prediction based on Logistic regression and effective antecedent rainfall［J］.The Chinese Journal of Geological Hazard and Control，2006，17(1):33-35.

［14］Miller S，Brewer T，Harris N.Rainfall thresholding and susceptibility assessment of rainfall-induced landslides:application tolandslidemanagementin StThomas，Jamaica［J］.Bull Eng Geol Environ，2009，68:539-550.

［15］CHANG K T，Chiang S H.An integrated model for predicting rainfall-induced landslides［J］.Geomorphology，2009，105:366-373.

［16］Ayalew L，Yamagishi H，Marui H，et al.Landslides in Sado Island of Japan:part II.GIS-based susceptibility mapping with comparisons of results from two methods and verifications［J］.Eng Geol 2005，81:432-445.

［17］汪东华.多元统计分析与SPSS应用［M］.上海:华东理工大学出版社，2010.WANG Donghua.Multivariate statistical analysis and application ofSPSS［M］.Shanghai:EastChina University of Science and Technology Press，2010.

［18］Klaus B， Bernd E， WulffP， etal.Multivariate Analysemethoden［M］.Springer Berlin Heidelberg，2005.