偏转翼前缘热流分布特征

许 考，陈连忠，刘 洋

（中国航天空气动力技术研究院，北京 100074）

0 引 言

作为高速飞行器重要的部件，在飞行过程中机翼要经受严酷的气动加热，尤其是前缘部位［1］。前缘部位热流评估的正确与否直接关系到翼前缘气动热试验能否顺利进行，更关系到飞行器设计的成败。

电弧风洞实验表明，在零偏转角的条件下，前缘上的热流最高处集中在前缘几何中心线（对称线）上。然而，为了对高速飞行器飞行方向进行有效控制，在飞行器飞行过程中机翼往往与来流方向有一定的偏转角度，即本文称之为偏转角。在来流方向不变的条件下，此时翼前缘几何中心线上的热流密度要发生变化，在同一截面上热流密度的最大值由几何中心变化到前缘的其它位置，称之为实际前缘线（该线为虚构的，供分析使用）。在来流一定的条件下，实际前缘线与机翼的迎风角、偏转角之间的关系是主要研究内容。 目前，关于翼前缘气动加热方面的研究主要集中在前缘附近的激波与底板边界层干扰及该区域的热流分布方面的研究［1-4］，翼身附近流动分离研究［5-6］，对翼前缘热流计算的工程算法主要为后掠圆柱的热流计算公式［7］及零偏转翼前缘热流工程算法［8］，而对于带有偏转角翼前缘最高热流变化及位置分布快速工程计算方法还未见报道，因此有必要对其开展研究，找出迎风角或偏转角变化时翼前缘上热流分布变化特征，特别是实际前缘线的变化，从而在有偏转角的翼（舵）前缘电弧风洞烧蚀试验中可以较准确地测量实际前缘线部位的烧蚀后退量。同样，在有偏转机翼的工程设计中可以快速找出翼前缘上最大热流分布位置。

首先利用理论分析来流在翼前缘上的矢量关系，找出在前缘弧面上最高热流位置处迎风角、偏转角及离心角（实际前缘线偏离中心线的角）之间的关系，并用实验来验证，找出前缘弧面上实际前缘线随迎风角及偏转角的变化规律。

1 问题分析

由后掠圆柱前缘的热流计算公式［5］可知，在来流参数不变的条件下对于0°偏转角的机翼来说，前缘弧面上热流最高位置位于前缘中心线上，即该位置处的法向速度分量最大。同样，对于偏转翼来说，前缘弧面上热流最高位置也位于弧面上某处法向速度分量最大的位置，因此有必要对来流进行矢量分析。

设喷管出口的某超声速自由来流，在靠近某一具有迎风角和偏转角的机翼前缘时，法向速度分量最大位置由前缘中心线上某处转移至与之夹角为ε的位置处，该来流在翼前缘上的热流密度最大，见图1中的A-A 截面。

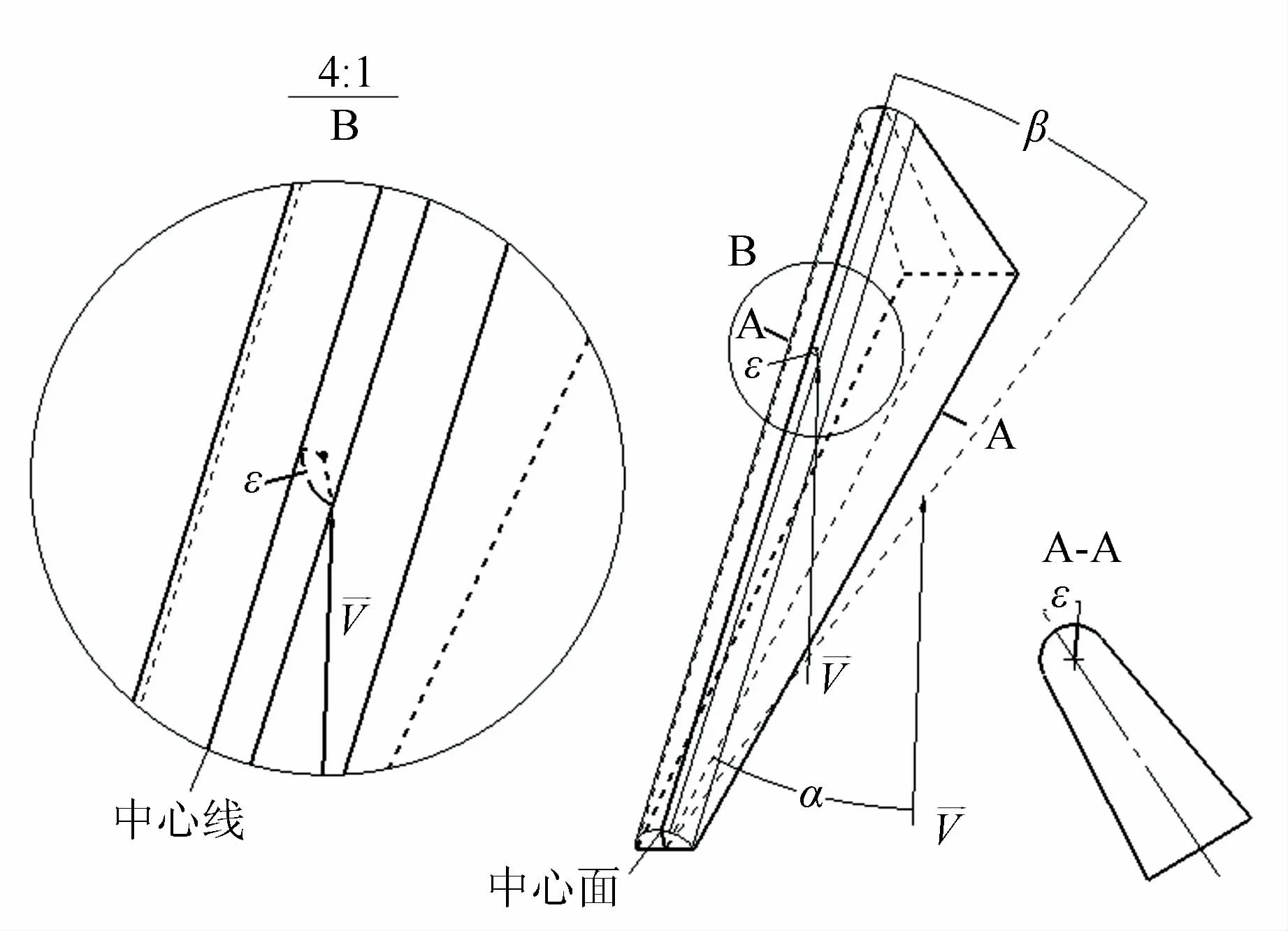
图1 偏转翼与来流的三维示意图Fig.1 The 3D sketch for some wing with some deflection and the coming flow

图1中来流方向与机翼的几何中心面夹角为α，即本文称之为翼的偏转角，β为翼前缘的迎风角，前缘上偏离前缘中心线的离心角为ε。流场矢量分析见图2。图2中取前缘上垂直于前缘中心线的某一截面作为分析对象，设来流正好落在该前缘弧面上某点位置。为来流的速度矢量，其两相互垂直的速度迎中分风用量角虚为方线向表两示及 ）相，互则垂，即直垂的直速=于度该分前＋量缘为上。 的同 截和样面， ，而（图在2平行于此截面。过O点作平行四边形BDEO，则OE与上述的前缘截面在同一平面内。同样，过O点作平行四边形ABFO，则OF同样与上述前缘截面在同一平面内。连接OF，由图中的矢量分解关系可以得，OB垂直于OF，F′在线OF上，tanα==，tanε==而OF′与OF在同一直线上，OE／／BD。无论点F与点F′是否重合，在来流条件不变的情况下，由于，和均为与迎风角有关的速度分量，故=或=，即tan（∠OEF）=tanε或tan（∠OEF′）=tanε，根据图2可以得：

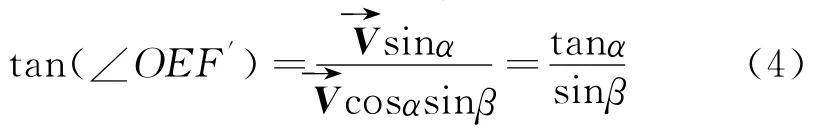
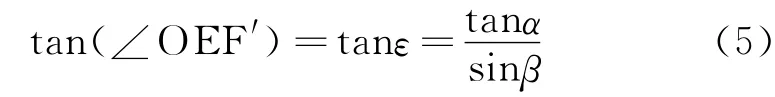
另外由于∠A′EO不可能为钝角且A′E⊥EO，故为O点位置处法向最大的速度分量，该处冷壁热流为最大（同截面上）。由上述推导同样可以看出略大于，即有偏转时O点的冷壁热流略大于无偏转时同截面的中心线上冷壁热流。

其中β＞0，式（5）与来流无关，最高热流位置仅与三个角度有关，而满足三个角度之间的关系只需在电弧风洞实验中按上述角度安装即可。

2 实验研究及验证

实验在中国航天空气动力技术研究院电弧风洞内完成，采用自由射流实验技术，其中气流总焓2000～10000 kJ／kg，喷管出口雷诺数Re＜4×106／m，实验中翼前缘半径8mm≤R≤20mm。翼模型安装时迎风角、偏转角及前缘上离心角ε之间的关系按式（5）计算。前缘中心线及与之对应的、垂直于前缘线的截面上的离心角ε位置处均设置热流计［9］，见图1。设翼前缘水平距离为L（L＜500mm），翼前缘中心线上冷壁热流密度为q1，前缘上离心角为ε位置处的前缘线上的冷壁热流密度为q2。在电弧风洞实验中，一方面受到加热器功率的限制，为了实现翼前缘试验所需的热环境状态，喷管的出口面积与喉道面积之比一般不是很大；另外，随着来流总焓的增加，比热比的降低会使得实际来流马赫数降低，故电弧风洞烧蚀试验中来流马赫数一般在Ma=2～6的范围内。

2.1 实验验证

图3表示气流总焓为2000kJ／kg时翼偏转角α=5°及0°时两热流比值分布情况。图中的纵坐标q1（2）／q2（1）表示q1／q2或q2／q1，横坐标中的X表示从前缘最前端开始沿着中心线方向的水平距离。

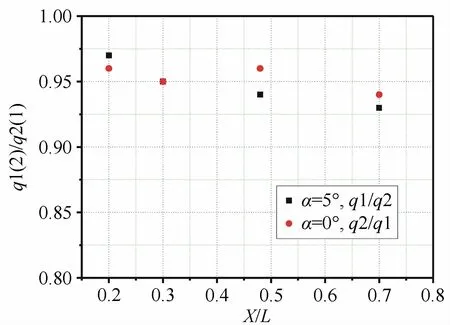
图3 气流总焓为2000kJ／kg时前缘热流分布Fig.3 The heat flux distribution（h 0=2000kJ／kg）

该状态下来流Ma=4.1，翼迎风角β=33°，前缘上离心角ε=9.2°位置设置热流计，来流雷诺数为Re=3×106／m。

由图3可以看出，α=5°时前缘上中心线处的冷壁热流与其对应位置处离心角为9.2°处的热流比值q1／q2在0.93～0.97，而且沿着流场方向略有降低，而对于零偏角时q2／q1与q1／q2基本相当，仅X／L=0.48时其比q1／q2高约0.02。总的来说，无论偏转角为0°还是5°两比值均在0.95左右波动。

图4表示气流总焓为4000kJ／kg时翼偏转角α=15°及0°时两热流比值分布情况（Ma=5.2，β=33°，ε=30°，Re=3.5×106／m）。可以看出，不论偏转角为15°还是0°，两热流比值均在0.77～0.81 范围内，其中X／L=0.25和0.70时q1／q2和q2／q1相差相对较大，但仅0.02，基本认为两比值是一致的。

图5表示气流总焓为8000kJ／kg时翼偏转角α=15°及0°时两热流比值分布情况（Ma=4.7，β=19°，ε=39.5°，Re=2.0×106／m）。图中明显可以看出，不论偏转角为15°还是0°，各测点的q1／q2和q2／q1均较接近。

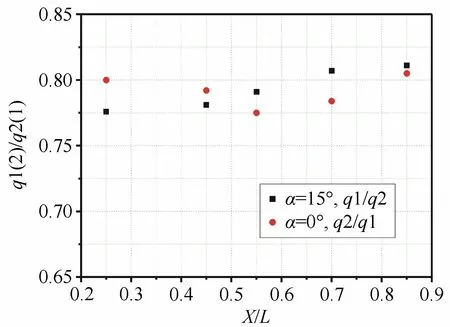
图4 气流总焓为4000kJ／kg时前缘热流分布Fig.4 The heat flux distribution（h0=4000kJ／kg）

图5 气流总焓为8000kJ／kg前缘热流分布Fig.5 The heat flux distribution（h o=8000kJ／kg）

图6表示气流总焓为10000kJ／kg时翼偏转角α=15°及0°时两热流比值分布情况（Ma=4.5，β=19°，ε=39.5°，Re=1.0×106／m）。图中可以看出，各测点的q1／q2 和q2／q1 的差值均小于0.03（X／L=0.72时差值为0.03），比较接近。

图6 气流总焓为10000kJ／kg前缘热流分布Fig.6 The heat flux distribution（h o=10000kJ／kg）

图7和8分别表示来流总焓为10000 kJ／kg时偏转角α=15°及0°、垂直于前缘的截面（见图1中AA）上ε=0°及39.5°位置处静压历程，该状态与图6中的相对应。

采用最大量程为10k Pa的绝对压力传感器测量该静压，传感器的精度为0.3%F·S。在测量过程中，先起动电弧风洞，待流场稳定后用作动筒将在流场区域以外的测压调试件迅速推入喷管出口处的流场之中，后停止电弧加热器，故图7和8中7.5s之前的压力均为加热器稳定阶段所测压力，7.5s时测压调试件进入流场，压力迅速增加。

由图中可以看出，当偏转角α=15°时ε=39.5°位置处静压比ε=0°高约1.1k Pa，而当偏转角α=0°时ε=0°位置处静压比ε=39.5°约高1.2kPa，这与图6中的热流比值是对应的。由该图还可以发现，有偏转时实际前缘线上压力略高于0°偏转时前缘中心线上的压力，这同样与第二部分分析是一致的。

图7 偏转角α=15°时前缘截面上静压历程Fig.7 The staticpressure history on the section of the leading edge with the deflection angle of 15°

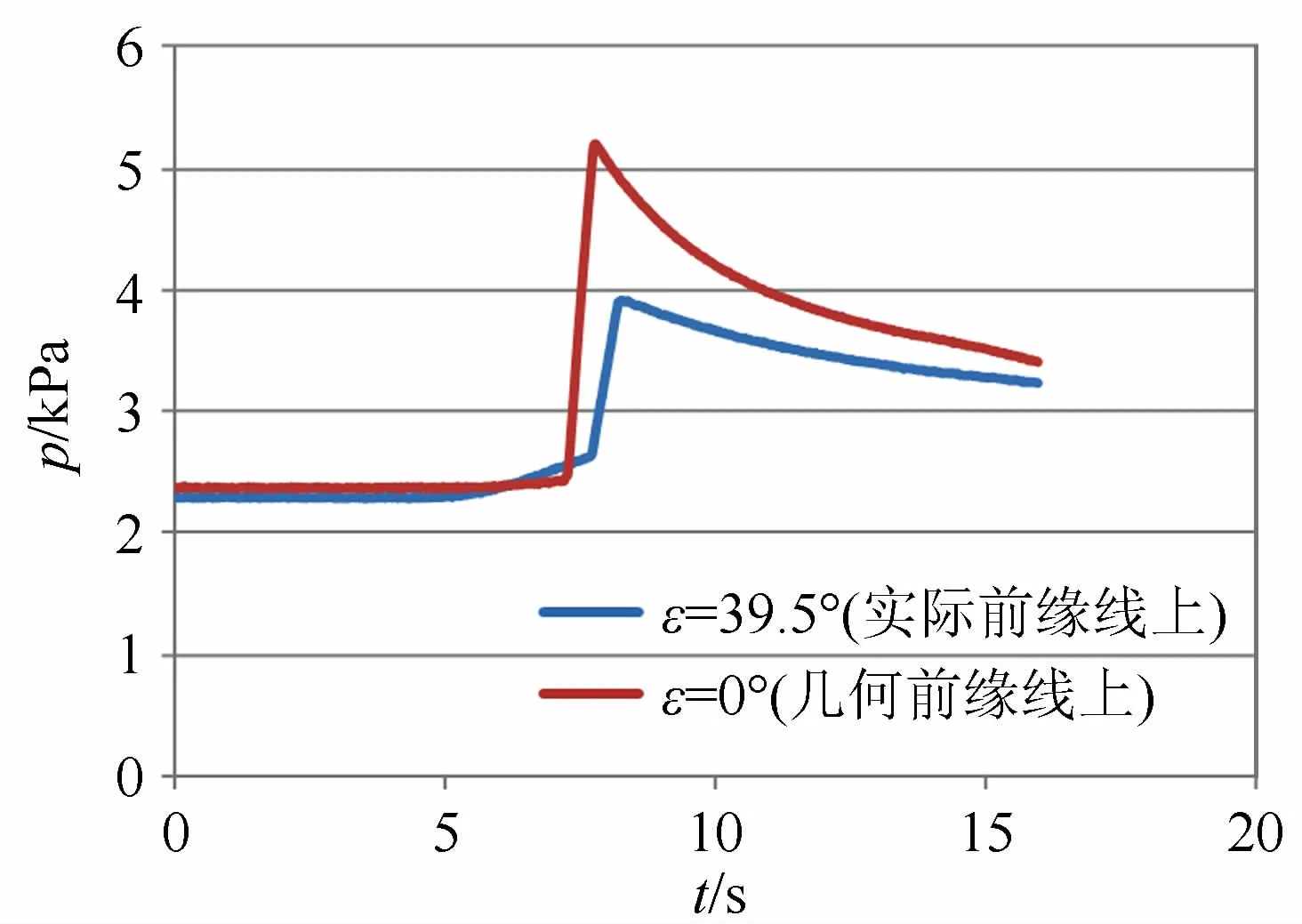
图8 偏转角α=0°时前缘截面上静压历程Fig.8 The static pressure history on the section of the leading edge with the deflection angle of 0°

2.2 工程算法及比较

由于垂直于前缘中心线的某一截面可以看作与之半径相等的球面上的一截面，因此，可用球面热流分布规律验证翼前缘中心线和实际前缘线上的冷壁热流的比例关系。Lee［10］利用修正牛顿压力分布和等熵外流条件得到了球面热流密度分布，其简化表达式为：

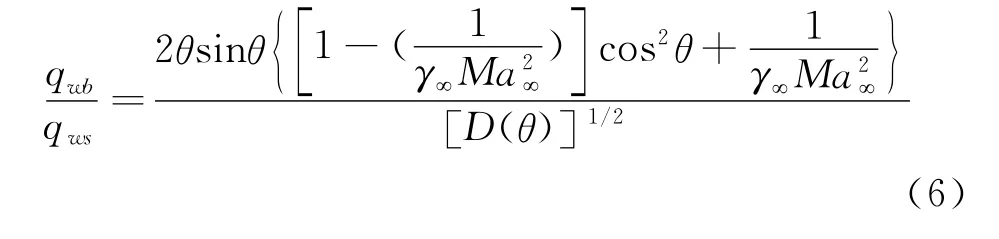
其中，

这里γ∞和Ma∞分别为喷管出口处来流的比热比和马赫数，θ为偏离中心点角度，与文中的ε一致。根据（6）式可以看出，γ∞和Ma∞对球面热流密度影响较小，θ则影响较大。根据该式计算上述实验条件下前缘中心线上与实际前缘线上热流密度比值，实验部分数值取距离喷管出口最近的一点，见表1。

由表1 可以看出，当气流总焓为10000 kJ／kg时，工程计算（式（6））与实验值相差最大，该热流密度的差值是实际前缘线热流密度的8%；气流总焓为2000kJ／kg次之，差值约占实际前缘线上的5%；其余的均较接近，基本在3%之内。由此可知，在上述条件下，式（5）基本上可以满足工程使用要求。

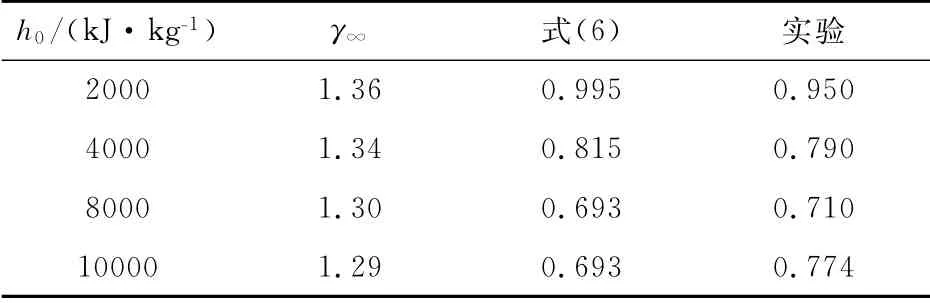
表1 前缘上热流密度实验与计算比较Table 1 Comparison between experiment and engineering calculation

3 偏转翼前缘实际前缘线变化

前面已证明式（5）能满足工程使用要求，根据该式可以看出，在迎风角不变的情况下，随着偏转角的增加，离心角越大，即实际前缘线不断偏离前缘中心线，见图9。而当偏转角不变时，随着迎风角的增加，离心角却减小，即实际前缘线向前缘中心线靠近，如图10所示。

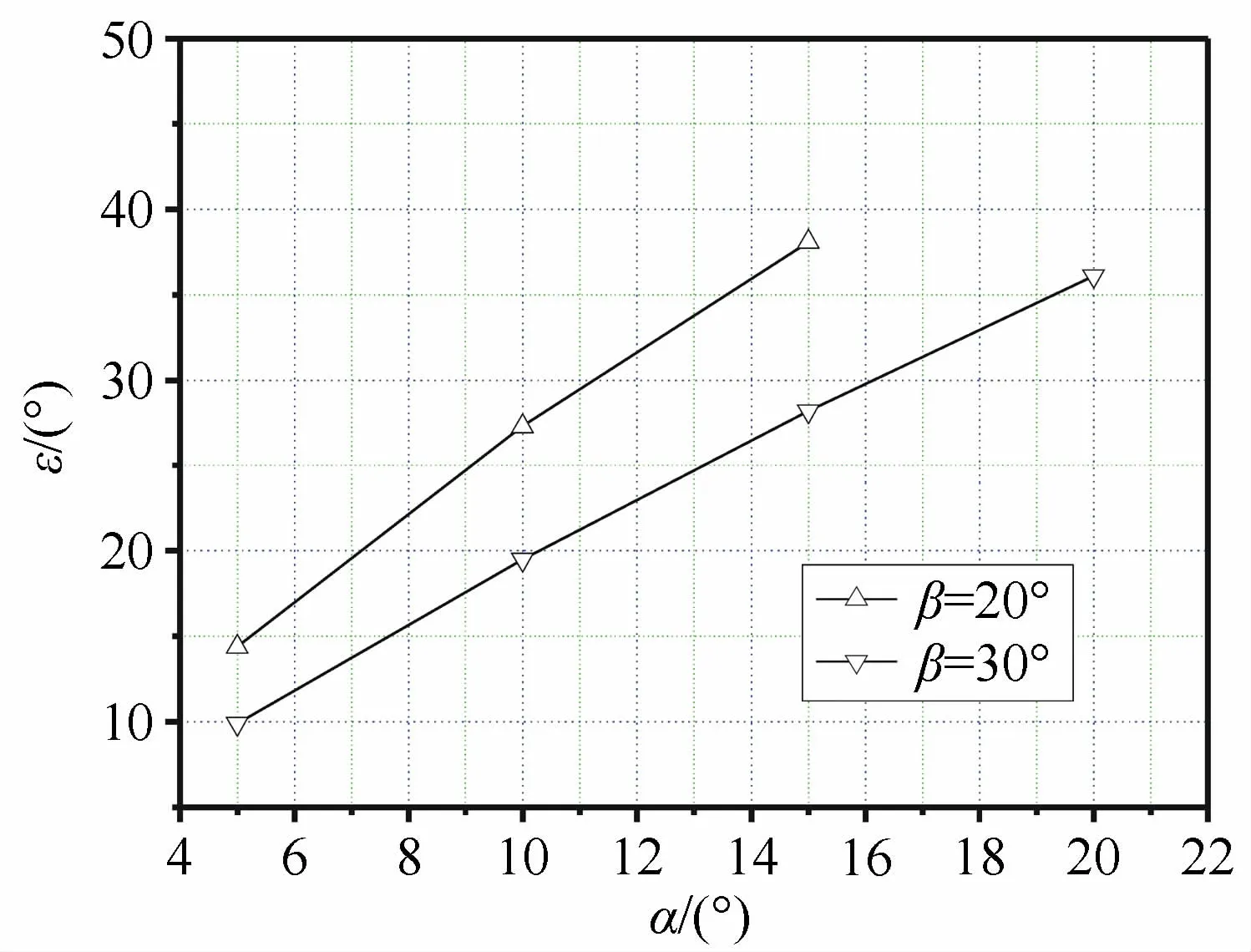
图9 离心角随偏转角变化Fig.9 The change of the deviation angle with the deflection angle

图10 离心角随迎风角变化Fig.10 The change of the deviation angle with the windward angle

4 结 论

通过上述分析，可以得出以下结论：

（1）式tanε=tanα／sinβ（β＞0）在本实验条件下（气流总焓2000kJ／kg≤h0≤10000kJ／kg，α≤15°，ε≤40°）可以基本满足工程使用，在确定迎风角和偏转角条件下，可快速计算出翼前缘上最大热流分布位置；

（2）在迎风角不变的条件下，随着偏转角的增加，实际前缘线（热流最高位置）逐渐偏离前缘中心线；

（3）当偏转角不变的条件下，随着迎风角的增加，实际前缘线逐步向前缘中心线靠近。

［1］ 李素循.激波与边界层主导的复杂流动［M］.科学出版社，2007，6：80.

［2］ 王世芬，王宇.尖前缘翼干扰区的壁面压力和热流率分布［J］.空气动力学学报，1995，13（4）：447-450.

［3］ MARCOD C，GIUSEPPE C R，RANCES Co B.An extrapolation from flight methodology for a Re-entry vehicle wing leading edge test in a plasma wind tunnel facility［R］.39thAIAA Thermophysics Conference，2007，6：3895.

［4］ 姜贵庆，张学军，王淑华，等.飞行器尖化前缘的热结构特性［J］.计算材料学，2007，4：8-11.

［5］ 邓学蓥，吴鹏，王延奎.前缘吹气控制舵面流动分离［J］.北京航空航天大学学报，2012，38（7）：853-856.

［6］ 孟宣市，蔡晋生，罗时钧，等.低背鳍对细长平板三角翼分离涡稳定性影响的研究［J］.实验流体力学，2012，26（3）：46-50.

［7］ RESHOLKOE，BECKWITH I E.Compressible laminar boundary layer over a yawed infinite cylinder with heat transfer and arbitrary prantl number［R］.NASC Rept，1379，1958.

［8］ 杨恺，高效伟.高超声速飞行器关键部位气动热计算［J］.计算力学学报，2012，29：14.

［9］ JOSE A Santos，ANUSHECH Nawaz，Ed Martinez，et al.Volumetric heat flux characterization experiments in the interaction heating facility at NASA Ames［J］.10th AIAA／ASME Joint Thermophysics and heat Transfer conference，Chicago，lllinois.2010，4785.

［10］LEES L.Laminar heat transfer over blunt nosed bodies at hypersonic flight speeds［J］.Jet Propulsion，1959，26（4）：259.