钢纤维自密实混凝土弯曲疲劳性能研究

蔡 军

（商洛学院 城乡发展与管理工程系，陕西商洛 726000）

国内外统计资料表明，耐久性不足是导致混凝土结构在正常使用状态下失效的最主要原因。为了解决日益严重的混凝土结构耐久性问题，日本东京大学的岗村甫教授开发了一种“不振捣的高耐久性混凝土”，称之为自密实高性能混凝土(Self-Compacting High Performance Concrete，简称SCHPC)。由于具有显著的优势，自密实混凝土被科学家们誉为“混凝土建筑技术中最具革命性的发展”[1-2]。钢纤维自密实混凝土(Steel Fiber Reinforced Self-Compacting Concrete， 简 称SFRSCC)是一种性能优良的新型复合材料，综合了自密实混凝土和钢纤维混凝土的优点。与普通混凝土相比，钢纤维自密实混凝土具有高耐久性的特点，同时具备优良的力学性能，在各个工程领域中的应用越来越广泛[3-6]。目前关于钢纤维自密实混凝土疲劳性能的研究，国内外还未见报道。为了进一步推广钢纤维自密实混凝土在各个工程领域中的应用，本文对钢纤维自密实混凝土的弯曲疲劳性能进行了试验研究，并对钢纤维自密实混凝土的疲劳性能进行了分析。

1 试验概况

本试验水泥采用42.5级普通硅酸盐水泥，粗骨料为粒径5-20 mm连续级配碎石，细骨料为中砂，细度模数为2.6，矿物掺合料为原状一级粉煤灰，减水剂采用南京水利科学研究院HLC型高效减水剂，钢纤维采用长度30 mm、长径比60的冷拔钢丝弓形钢纤维，抗拉强度为1000 MPa。材料配合比见表1。

表1 钢纤维自密实混凝土配合比 单位：(kg·m-3)

按照《自密实混凝土应用技术规程》（CECS203:2006），分别采用坍落扩展度试验和V型漏斗试验对钢纤维自密实混凝土的工作性能进行检测，如图1、图2所示。

图1 坍落扩展度试验示意图

图2 V型漏斗形状及尺寸

弯曲疲劳试验采用100 mm×100 mm×400 mm的梁形试件，采用三分点加载方式，梁跨度为300 mm，试验加载设备为国产SDS300电液伺服动静万能试验机。应力水平S取0.90、0.85、0.80和0.75，疲劳循环特征值R取0.1，正弦波加载，如图3所示。

图3 正弦型循环荷载

各参量关系为

式中，S——应力水平；

Pmax——所施加最大荷载；

Pmin——所施加最小荷载；

Pu——静载试验极限荷载；

R——疲劳循环特征值。

当S＞0.80时，荷载频率取5 Hz，当S≤0.80时，荷载频率取10 Hz。进行疲劳试验前，通过静载试验测得极限静荷载Pu，作为疲劳加载的依据。疲劳试验的试件数量见表2。

表2 疲劳试验的试件数量

2 试验结果与分析

2.1 工作性能

测得的钢纤维自密实混凝土坍落扩展度值为698 mm，V形漏斗时间为13 s，均达到规范规定的要求[6-7]。

2.2 疲劳试验结果

钢纤维自密实混凝土疲劳试验结果见表3。

2.3 疲劳寿命概率分析

在同一循环荷载作用下，疲劳寿命的分布规律可以由威布尔频率函数表示

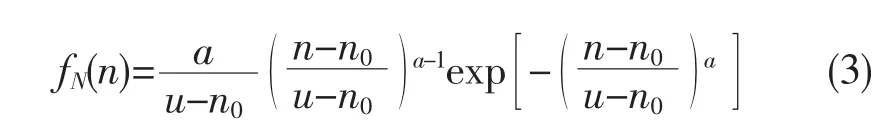
式中，a——威布尔形状参数；

u——特征寿命参数；

n0——最小寿命参数。

由于材料的离散特性，在威布尔频率函数中取最小寿命参数n0为零[8-9]，分布函数简化为两参数威布尔频率LN(n)函数，则存活率可表示为

对方程取两次自然对数得

令 Y=1n[1n(1/LN)],X=lnn,β=alnu。可得

式(6)可检验一组试验数据是否服从两参数威布尔分布，如果试验数据的回归分析结果表明，Y与X之间呈现很好的线性关系，则试验数据服从两参数威布尔分布的假设成立，反之假设不成立。钢纤维自密实混凝土疲劳寿命威布尔分布拟合曲线如图4所示，回归结果表明，1n[1n(1/LN)与lnn之间呈现良好的线性关系，说明钢纤维自密实混凝土疲劳寿命服从两参数威布尔分布。

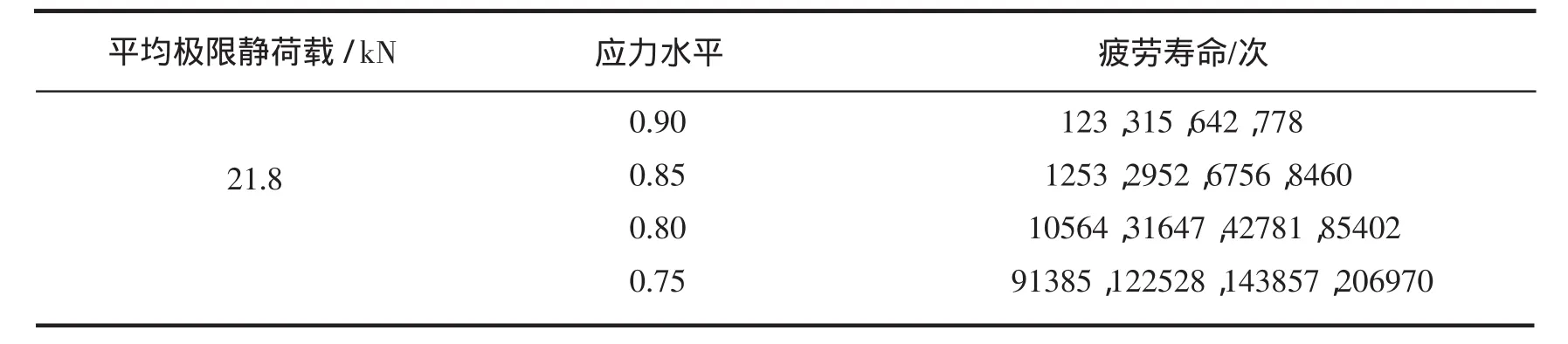
表3 钢纤维自密实混凝土疲劳寿命

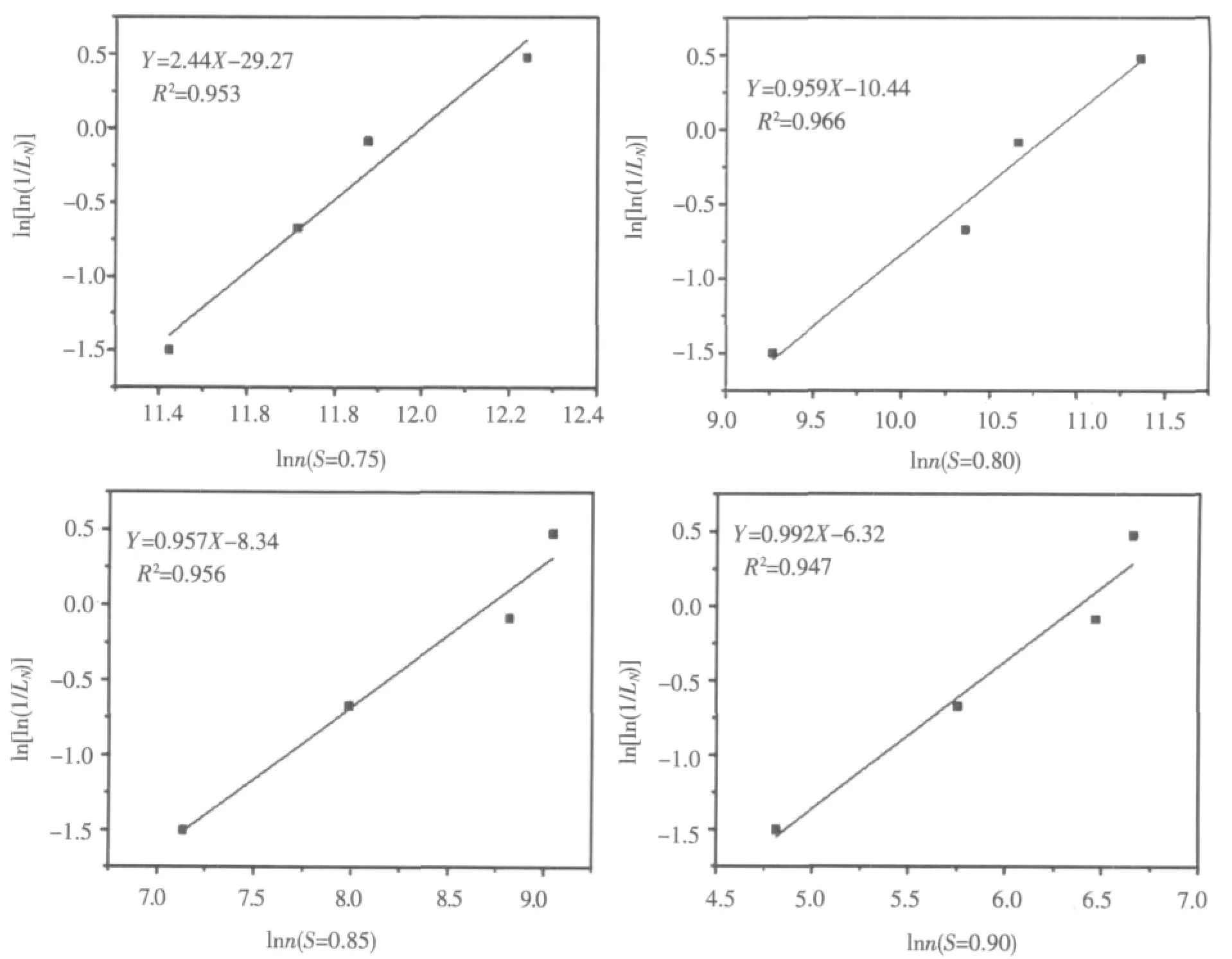
图4 钢纤维自密实混凝土疲劳寿命威布尔分布拟合曲线

2.4 疲劳方程

本文疲劳方程形式采用双对数疲劳方程

不同存活率下疲劳方程的回归参数a和b见表4。

表4 不同存活率下疲劳方程的回归参数

2.5 疲劳性能分析

材料的疲劳性能取决于疲劳方程中的回归参数a，参数a反映疲劳曲线的高度，a值越大，疲劳曲线越高，则材料的疲劳性能越好[10]。参照文献[10]对不同类型混凝土的弯曲疲劳性能进行了试验研究，疲劳试验采用100 mm×100 mm×400 mm梁形试件，各种类型混凝土存活率为0.9的双对数疲劳方程回归参数a见表5。

表5 各种类型混凝土疲劳方程的回归参数

从疲劳方程回归参数结果可以看出，对于相同存活率下的双对数疲劳方程，钢纤维自密实混凝土的回归参数a值相比普通混凝土提高10.2%，钢纤维自密实混凝土的疲劳性能相比普通混凝土明显增强。

3 结论

本文对钢纤维自密实混凝土的弯曲疲劳性能进行了试验研究，建立了在不同失效概率下的P-S-N疲劳方程，填补了这方面研究的空白。研究结果表明，钢纤维自密实混凝土的疲劳寿命符合两参数威布尔分布，与普通混凝土相比，钢纤维自密实混凝土的疲劳性能明显增强。

[1]安雪晖,黄绵松,大内雅博,等.自密实混凝土技术手册[M].北京:中国水利水电出版社,2008.

[2]桂苗苗.国内外自密实混凝土的标准概况与比较[J].材料导报,2011(3):97-100.

[3]丁一宁,刘思国.钢纤维自密实混凝土弯曲韧性和剪切韧性试验研究[J].土木工程学报,2010(11):55-63.

[4]刘思国,刘军其,姜恒志,等.钢纤维自密实混凝土抗压强度估值模型[J].混凝土,2012(8):97-99.

[5]张春晓,蔡灿柳,丁庆军.钢纤维自密实混凝土抗离析性能试验研究[J].施工技术,2011(11):48-50.

[6]EFNA R C.Specifications and guidelines for selfcompacting concrete[S].London,2002.

[7]中国建筑标准设计研究院.自密实混凝土应用技术规程（CECS203:2006）[M].北京:中国计划出版社,2006.

[8]易 成,谢和平,孙华飞.钢纤维混凝土疲劳断裂性能与工程应用[M].北京:科学出版社,2003.

[9]石小平,姚祖康,李 华,等.水泥混凝土的弯曲疲劳特性[J].土木工程学报,1990,23(3):11-22.

[10]LiH,ZhangM H,Ou JP.Flexuralfatigue performance of concrete containing nano-particles for pavement[J].International Journal of Fatigue,2007,29(7):1292-1301.