粗砂浆体水平管道流动水力坡度预测研究

赵利安，许振良

(辽宁工程技术大学 矿业学院，辽宁 阜新 123000)

在我国的水库、港口以及江河湖泊等疏浚工程中，泥沙的管道输送是一种重要的输送方法.而输沙管道，尤其是粗砂管道水力坡度的预测，对于浆体泵的选择以及各种输送参数的确定具有重要意义，是管道输送工程的重要研究内容.因此，众多学者对输沙管道的水力坡度进行了研究［1－5］.这些研究中，有的基于经验公式，有的基于前人研究的理论推导，但都未能阐明颗粒，尤其是粗颗粒与细颗粒在管道中的运动规律.本文通过分析粗砂颗粒受力平衡，来研究粗砂颗粒受力情况，在此基础上，研究管道中粗砂浆体水力坡度预测模型.

1 水平管道粗砂运动受力分析

固体颗粒在管道中完成加速过程以后，沉降性浆体就会达到一个稳定的流动状态，水、固体颗粒和沉降性浆体的速度将达到一定的值.此时，固体颗粒的加速度dvs/dt=0，则可以得到下式［6］:

式中:fD为流体对颗粒的拖曳力为阻力系数，V为清水平均流速，V为粗砂ws颗粒平均速度;ρ为清水密度;de为颗粒直径;fh为其他颗粒的干涉力，fh=为颗粒的管内浓度分布;Rep为颗粒雷诺数，计算方法见有关文献［7］，α和β为颗粒斯万逊常数，对于球形颗粒，其值分别为0.662 6和5.368;n为指数，计算方法参照文献［6］;ff为颗粒与管道底部的摩擦力为颗粒与管道底部的摩擦系数，g为重力加速度.K4为处于滑跳移的颗粒占总颗粒的比例，当颗粒处于完全滑跳移运动时，K4=1;当颗粒处于完全悬浮运动时，K4=0;当颗粒处于部分悬浮，部分滑跳移运动时，K4=11 Vt/Vm，其中Vt为颗粒沉降终速度，Vm为浆体平均速度.

对于小颗粒的情况，式(1)是成立的，而对于大颗粒的情况，有必要进行检验.本文采用朝仓国臣等［6－9］学者的粗砂试验数据进行计算，试验条件见表1.

表1 用于验证粗颗粒受力平衡的若干流动试验条件Tab.1 Test conditions used in testing force balance equation for coarse sand

计算结果如图1所示.图1表明，根据公式计算的粗砂颗粒的干涉力fh的值普遍小于水流对颗粒的拖曳力和颗粒受到的摩擦力之差.因此，对于粗颗粒，式(1)存在较大的偏差，偏差存在的原因在于干涉力fh的计算不准确.此处采用修正系数L对干涉力进行修正，则式(1)变为:

通过对若干专家试验数据的分析，发现粗砂颗粒(密度不变)的体积浓度C，浆体平均速度Vm，颗粒粒径的de均会对修正系数产生影响［9－10］.考虑到浓度因素习惯用1－C表示，且此处颗粒为粗砂颗粒，管道直径D的影响也应考虑，以及L为无量纲常数，则系数L的形式为:

利用表1中专家的试验数据，采用式(3)计算了不同条件下的修正系数L值，并进行了数据拟合，结果见图2.最后得到修正系数L的表达式为:

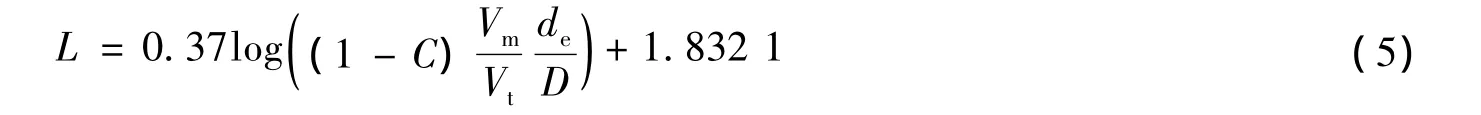
另外，从前面的计算可知，大多数情况下，修正系数L的值大于1.

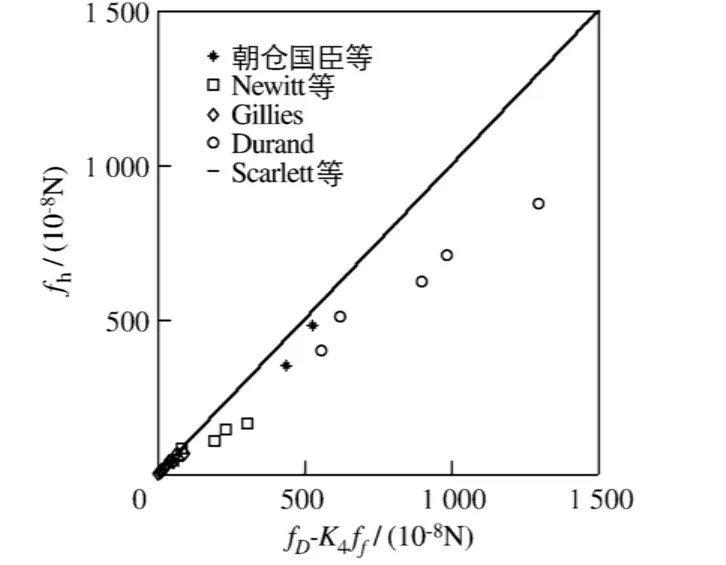
图1 力平衡方程的计算Fig.1 Calculation of force balance equation D)

图2 系数L和(1－C)(Vm/Vt)(de/D)的关系Fig.2 Relation between coefficient L and(1－C)(Vm/Vt)(de/

研究发现颗粒直径超过0.2 mm后，颗粒的受力情况和运动情况与粒径小于0.2 mm的差异较大［9］.由于式(5)是从粒径为0.29～2.04 mm的粗砂试验数据得出的，故式(5)只适用于粒径大于0.2 mm的粗砂.

2 粗砂管内流动水力坡度计算模型推导

当管道中的水流处于紊流状态时，水力坡度可以用下式来表示:

式中:λ为达西阻力系数;V为清水与粗砂颗粒发生动量交换前的速度.

对于粗砂浆体而言，当粗砂颗粒处于完全悬浮、部分处于悬浮，部分处于滑、跳移以及颗粒全部滑、跳移运动时，不能用式(6)来计算阻力损失.根据许振良等［6］的研究，以平均流速Vm流动的沉降性浆体可以被看作是以平均速度V流动的清水.更加确切地说，如果管段两边存在的压力差能够使清水以速度V流动，则当粗砂颗粒群介入后，就只能使浆体以速度Vm向前移动.因此，当沉降性浆体以速度Vm在管道中流动时所产生的水力坡度可以认为是以速度V在管道中流动的清水的水力坡度，其原理可以用图3所示的等效阻力模型来理解.

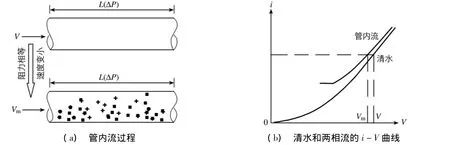
图3 等效阻力模型原理Fig.3 Principles of equivalent resistance model

由流体对颗粒的拖曳力fD的表达式可以得到:

式中:颗粒的干涉力fh和ff以及滑移速度Vw－Vs和阻力系数CDr均为浓度分布q的函数［6］.

当以单位水平管道为研究对象时，设管道内的平均管内浓度为q，浆体平均速度为Vm，粗砂颗粒平均速度为Vs，水流平均速度为Vw，根据上面式(5)～(7)，滑移速度计算式(7)变为:

利用式(8)，可通过迭代法求解，得到平均滑移速度的值.

根据文献［9］，存在以下关系:

式中:δ为粗砂颗粒的密度与液体(水)的密度之比;K3为常数，取值3.742;λ为达西阻力系数，可用阿里特苏公式计算［5］;ψ(1)，La的计算方法见有关文献［6，11］.

根据式(8)、(9)和(10)，可以求出固体颗粒平均速度Vs，液体平均速度Vw，及动量交换前流体的平均速度V.将求出的速度V代入式(6)，就可以得到粗砂浆体管道流动的水力坡度.

3 粗砂管内流动水力坡度计算模型检验

在水平管道中，采用Durand等专家学者的粗砂试验数据，对前面提出的粗砂粒浆体水力坡度计算模型进行检验，具体参数见表2.

表2 用于验证水平管道水力坡度的试验参数Tab.2 Test parameters for verifying model of hydraulic gradient of horizontal pipe

颗粒处于各种状态时，水力坡度计算值和试验值的比较见图4，其中，图4(a)为颗粒处于完全悬浮状态时的水力坡度计算值和试验测定值的对比，从图中可以看出，计算值和试验测定值的偏差均在10%以内;图4(b)为颗粒处于完全滑跳移时，除个别点的误差较大外，大多数的偏差小于10%;图4(c)为颗粒处于部分悬浮、部分滑跳移时，大多数的偏差小于10%.

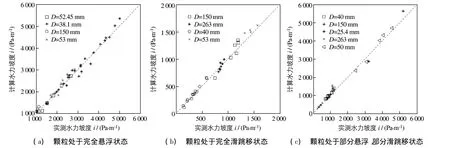
图4 水力坡度计算值与实测值比较Fig.4 Comparison between measured and calculated values of hydraulic gradient

图5为利用Gillies和Bonnington等专家的试验数据计算的不考虑修正系数L(即L=1)和考虑系数L两种情况下水力坡度的比较.可见，不考虑系数L时，计算值和实测值的最大偏差为19%;考虑系数L时，计算值和实测值的最大偏差为7.6%.从图5可以看出，考虑修正系数L后，水力坡度的计算值相对增大，总体上更加接近实测值.

图5 系数L对水力坡度的影响Fig.5 Influence of coefficient L on hydraulic gradient

4 结语

粗砂水平管道流动时，颗粒所受干涉力需要用系数修正;模型计算值与实测值的偏差基本小于10%，且考虑修正系数L后，水力坡度的计算值相对增大，更接近实测值.文中提出的粗砂颗粒水力坡度模型对于粗砂浆体管道输送技术具有一定参考价值.

［1］倪福生，齐帜，赵立娟.管道输沙两层流动模型分界位置的确定［J］.中国港湾建设，2008(1):13-15.(NI Fu-sheng，QI Zhi，ZHAO Li-juan.Determination of location of interface in two level flow model for sediment transport in pipelines［J］.China Harbour Engineering，2008(1):13-15.(in Chinese))

［2］罗大鑫.管道排沙特性试验研究［D］.天津:天津大学，2009:41.(LUO Da-xin.Experimental study on flushing characteristics the sediment with pipeline［D］.Tianjin:Tianjin University，2009:41.(in Chinese))

［3］王英杰，阳宁，金星.泥沙管道输送试验系统的研制及分析［J］.人民黄河，2012，34(2):34-38.(WANG Ying-jie，YANG Ning，JIN Xing.Research and analysis on experimental system of sediment transport in pipelines［J］.Yellow River，2012，34(2):34-38.(in Chinese))

［4］张雪兰，孙西欢，李永业，等.浅谈浆体管道输送阻力损失研究现状［J］.山西水利，2011(1):38-42.(ZHANG Xuelan，SUN Xi-huan，LI Yong-ye，et al.Research status of pipeline resistance loss of slurry transportation［J］.Shanxi Water Resources，2011(1):38-42.(in Chinese))

［5］叶坚，夏建新，MALCZEWSKA BEATA.水平管道水力输送粗粒物料的阻力损失研究［J］.金属矿山，2011(7):12-18.(YE Jian，XIA Jian-xin，MALCZEWSKA BEATA.Study on the resistance loss of hydraulic transport for coarse particles in horizontal pipeline［J］.Metal Mine，2011(7):12-18.(in Chinese))

［6］许振良.非均质流速度分布与水力坡度的研究［D］.沈阳:东北大学，1999.(XU Zhen-liang.Study on the velocity profile and hydraulic gradient of heterogeneous flow［D］.Shenyang:Northeastern University，1999.(in Chinese))

［7］张士林.浆体管道淤积流速数值计算方法研究［J］.水力采煤与管输，2011(4):6-9.(ZHANG Shi-lin.Research on numerical calculation method of deposition critical velocity in slurry pipeline［J］.Hydraulic Coal Mining ＆ Pipeline Transportation，2011(4):6-9.(in Chinese))

［8］GILLIES R G.Pipeline flow of coarse particle slurries［D］.Canada:Saskatchewan，1993.

［9］赵利安.大颗粒浆体管内流动规律研究［D］.阜新:辽宁工程技术大学，2011.(ZHAO Li-an.Study on flow law of large particle slurry in pipeline［D］.Fuxin:Liaoning Technical University，2011.(in Chinese))

［10］王铁力，赵利安.浆体管道中大颗粒干涉力研究［J］.洁净煤技术，2011(1):122-125.(WANG Tie-li，ZHAO Li-an.Study on interference force to large suspended particles in slurry pipeline［J］.Clean Coal Technology，2011(1):122-125.(in Chinese))

［11］张士林，许振良，邵龙潭.浮游界限速度的求解方法研究［J］.哈尔滨工业大学学报，2006，38(2):279-281.(ZHANG Shi-lin，XU Zhen-liang，SHAO Long-tan.Research of confirming float critical velocity in slurry［J］.Journal of Harbin Institute of Technology，2006，38(2):279-281.(in Chinese))