改进Elman神经网络在径流预测中的应用

崔东文

(云南省文山州水务局，云南 文山 663000)

河川径流受多种因素的影响和制约，表现出复杂、随机、多维等特性，探寻能够表征径流特性、预测精度高的模型对河川径流预测具有重要的现实意义和应用价值［1］.目前，径流的预测方法主要有时间序列、回归分析、模糊模式、小波分析、集对分析等，均在径流预测预报中取得了一定的成效.人工神经网络(Artifical Neural Network，ANN)具有较强的非线性映射能力、鲁棒性、容错性和自适应、自组织、自学习等许多特性，适宜解决高维、非线性系统问题，在这类智能算法中运用最为广泛;BP网络(Back-Propagation Network，BP)是ANN常用的神经网络模型之一，广泛运用于径流预测［2－6］.然而，BP神经网络是一种静态的前向型网络，将其运用于与时间序列有关的径流预测中存在着关键性缺陷，且BP网络存在着学习收敛速度慢、易陷入局部极值等不足，极大地制约了BP网络在径流预测中的精度和泛化能力.Elman网络是一种典型的动态神经网络，它是在BP网络的基础上，结构单元引入固定反馈环节，从而使系统具有适应时变特性的能力，使预测性能优于BP网络，进而改善系统的动态性能［7－8］，但由于Elman网络是在BP网络的基础上改进而来，也采用BP算法进行权值修正，因此同样存在着学习速度较慢、易陷入局部极小值等缺点.为此，本文提出一种基于遗传算法(Genetic Algorithm，GA)优化Elman神经网络连接权值的GA-Elman多元变量年径流预测模型，以新疆伊犁河雅马渡站径流预测为例进行实例分析，并构建传统Elman，传统BP和GA-BP多元变量年径流预测模型作为对比模型，预测结果与文献IEA-BP网络模型预测结果对比，旨在为GA-Elman模型在水文预测预报中的应用提供参考.

1 GA-Elman径流预测模型

1.1 Elman神经网络

动态递归神经网络是一种极具潜力系统预测工具，而Elman网络是动态递归神经网络中结构最为简单、运算量小、适合实时系统辨识的动态递归网络.Elman神经网络是Elman于1990年提出的，该模型是在前馈式网络的隐含层中增加了一个承接层，作为延时算子以达到记忆的目的，从而使系统具有适应时变特性的能力，能够更生动、更直接地反映系统的动态特性.与BP网络本质上的区别是Elman网络既有前馈连接，又有反馈连接，能有效克服BP网络不具备动态特性的缺点［7－10］.Elman网络结构见图1.

Elman神经网络一般分4层:输入层，隐含层(中间层)，承接层和输出层，如图1所示，输入层、隐含层、输出层的连接类似于前馈式网络，输入层单元仅起信号传输作用，输出层单元起线性加权作用.隐含层单元的传递函数可采用线性或非线性函数，承接层用来记忆隐含层单元前一时刻的输出值并返回网络输入，可以认为一步延时算子.Elman神经网络的特点是隐含层的输出通过承接层的延迟与存储，自联到隐含层的输入，使其对历史状态数据具有敏感性，增加了网络处理动态信息的能力，达到动态建模的目的.Elman网络同样可以以任意精度逼近任意非线性映射，工程中主要用于动态预测［11－12］，但在函数逼近、模式识别等方面均有应用［7］.Elman网络的非线性状态空间表达式为:

图1 Elman神经网络模型结构Fig.1 Elman neural network model structure

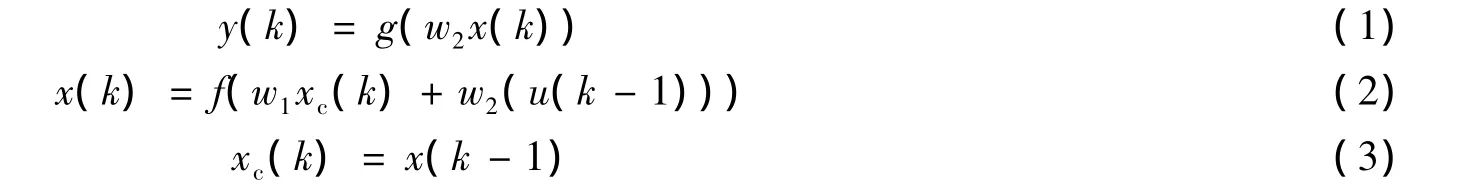
式中:y为m维输出结点向量;x为n维中间层结点单元向量;u为r维输入向量;xc为n维反馈状态向量;w3为中间层到输出层连接权值;w2为输入层到中间层连接权值;w1为承接层到中间层的连接权值;g()为输出神经元的传递函数，是中间层输出的线性组合;f()为中间层神经元的传递函数，常采用S函数.

Elman神经网络也采用BP算法进行权值修正，学习指标函数采用误差平方和函数.表达式为

1.2 GA-Elman 算法

遗传算法是由美国Michigan大学的John Holland教授在20世纪60年代提出，它是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法.遗传算法是将问题的求解表示成“染色体”，将其置于问题的“环境”中，根据适者生存的原则，从中选择出适应环境的“染色体”进行复制，即再生(reproduction，selection)，通过交叉(crossover)、变异(mutation)两种基因操作产生出新一代更适合环境的“染色体”群，这样不断改进，最后收敛到一个最适合环境的个体上，求得问题的最佳解.由于最好的染色体不一定出现在最后一代，开始时保留最好的染色体，如果在新的种群又发现更好的染色体，则用它代替原来的染色体，进化完成后，这个染色体可看作是最优化的结果.遗传算法可归纳为遗传运算(交叉与变异)和进化运算(选择)两种运算过程［13］.GA 与 Elman神经网络均具有极强的解决问题的能力，二者相结合，形成GA-Elman算法，该算法将遗传算法的全局寻优能力与Elman算法的指导性搜索思想相结合，既克服了寻优中的盲目性，又避免了局部收敛情况的发生，使网络性能得到极大的改善［14］.遗传算法优化Elman神经网络算法流程［15］如图2 所示.

图2 GA优化Elman神经网络算法流程Fig.2 GA optimization Elman neural network algorithm

GA-Elman算法的具体实现步骤如下:

(1)初始化种群P，包括交叉规模、交叉概率(Pc)、突变概率(Pm)以及对网络权值和阈值初始化，进行实数编码，初始种群n(视实际应用选择数值大小).

(2)计算每个个体评价函数，并将其排序，按下式概率值选择网络个体:

式中:fi为个体i的适配值，用误差平方和E来衡量，即

式中:i为染色体数，i=1，2，…，n;o 为输出结点数，o=1，2，…，q;k 为学习样本数，k=1，2，…，m;γo 为网络实际输出;d为期望输出.

(3)以交叉概率Pc对个体Gi和Gi+1进行交叉操作，产生新个体G'i和G'i+1，没有进行交叉操作的个体直接进行复制.

(4)利用变异概率Pm突变产生Gj的新个体G'j.

(5)将新个体插入到种群P中，并计算新个体的评价函数.

(6)判断评价函数是否满足结束条件.如果找到满意个体，则结束;否则转到(3)进入下一轮运算.

(7)算法结束，达到预先设定的性能指标后，将最终群体中的最优个体解码即可得到优化后的网络连接权值系数.

(8)将优化得到的网络连接权值系数赋值给Elman网络进行训练及预测输出.

2 实例分析

2.1 数据来源

为验证GA-Elman网络模型的有效性，以新疆伊犁河雅马渡站的流量预测为例.数据来源参见表1［16］.

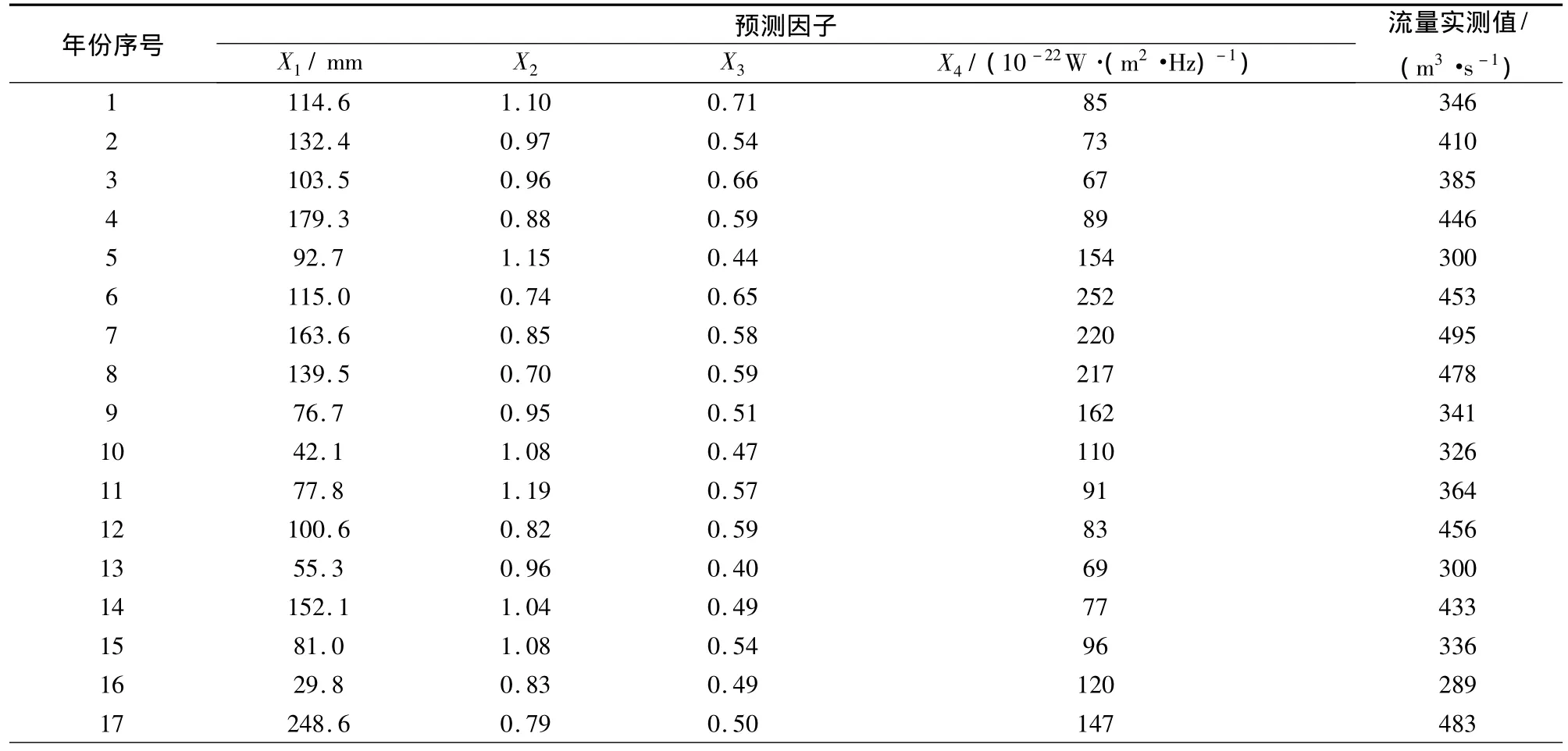
表1 新疆伊犁河雅马渡站实测流量及预报因子Tab.1 The measured flow and prediction factors of Yamadu hydrometric station in Ili River in the Xinjiang

(续表)

影响径流预测的4个预报因子特征值中，X1为前一年11月至当年3月伊犁气象站的总降雨量;X2为前一年8月欧亚地区月平均纬向环流指数;X3为前一年6月欧亚地区月平均径向环流指数;X4为前一年6月2 800 MHz太阳射电流量.

为便于与文献［16］比较，将表1中前16年的资料作为GA-Elman，传统Elman，传统BP以及GA-BP网络模型的训练样本，后7年资料进行预测检验.

2.2 径流预测的实现

2.2.1 数据处理 采用以下方法将各指标数据无量纲化到［0.1，0.9］之间，有利于网络训练.公式如下:

2.2.2 网络训练 本文基于MATLAB软件环境和谢菲尔德(Sheffield)遗传算法工具箱，创建及训练GAElman，传统Elman，传统BP以及GA-BP网络模型进行年径流预测.以表1中的4个预测因子作为网络输入向量;以流量实测值作为输出向量，构建4输入1输出的预测模型.本例兼顾拟合精度和预测精度，经反复调试，在下述参数设置条件下，GA-Elman，传统Elman，传统BP以及GA-BP模型具有较好的预测效果.

传统BP模型:由于目前BP网络隐含层神经元数的选取没有统一原则，本文采用较为普遍的Kolmogorv定理确定隐层单元数，最终确定BP网络结构为4－4－1，隐含层和输出层传递函数分别采用tansig和purelin，训练函数采用traingdx(该算法具有附加动量和自适应调整算法的优点，在一定程度上能有效避免收敛速度慢、陷入局部极值)，学习速率为0.1，设定期望误差为0.03，最大训练轮回为200次.

传统Elman模型:由于Elman网络是在BP网络的基础上改进而来，本文兼顾模型间的公平比较原则及预测精度，最终确定Elman模型结构、隐含层和输出层传递函数、训练函数、学习速率与最大训练轮回均与上述传统BP模型相同，设定期望误差为0.017.

GA-BP模型:同样基于公平原则，GA-BP模型的网络结构、隐含层和输出层传递函数、期望误差、最大训练轮回数等均与上述传统BP模型相同，在此条件下运用GA来优化BP神经网络的初始权值和阈值.GA参数设置为:种群规模为5，进化次数为100次，交叉概率为0.1，变异概率为0.05.

GA-Elman模型:基于模型间的公平比较原则及预测效果，GA-Elman模型的网络结构以及传递函数等所有参数设置均与上述GA-BP模型参数设置相同.

2.2.3 性能评价 选取平均相对误差eMRE和最大相对误差eMaxRE作为模型的评价指标.评价指标计算公式如下:

2.3 结果及分析

利用训练好的GA-Elman，传统Elman，传统BP以及GA-BP模型对新疆伊犁河雅马渡站进行年径流拟合及预测，结果见表2和3.

表2 新疆伊犁河雅马渡站流量拟合结果及其比较Tab.2 Flow fitting results and their comparison with the measured data at Yamadu hydrometric station in Ili River in the Xinjiang

表3 新疆伊犁河雅马渡站流量预测结果及其比较Tab.3 Flow prediction results and their comparison with the measured data at Yamadu hydrometric station in Ili River in the Xinjiang

分析表2和3可以得出以下结论:

(1)在相同网络结构、传递函数、训练函数等条件下，GA-Elman网络模型的拟合平均相对误差、拟合最大相对误差、预测平均相对误差以及预测最大相对误差均优于传统Elman、传统BP以及GA-BP模型，模型精度由高到低依次是:GA-Elman模型、GA-BP模型、传统Elman模型、传统BP模型，表明遗传算法能有效优化Elman和BP网络的初始权值和阈值.

(2)与文献［16］提出的IEA-BP模型预测结果相比，GA-Elman模型的拟合平均相对误差为6.78%，略高于IEA-BP模型的6.62%，拟合最大相对误差为18.51%，小于IEA-BP模型的22.19%;GA-Elman模型的预测平均相对误差为4.83%，小于IEA-BP模型的5.14%，预测最大相对误差为11.92%，略大于IEA-BP模型的10.66%;(2个模型)总体平均相对误差为5.80%，总体最大相对误差为18.51%，均优于IEA-BP模型的5.88%，22.19%;综合比较而言，GA-Elman模型预测效果略优于IEA-BP模型，表明本文提出的GA-Elman模型用于多元变量年径流预测是合理可行的，模型具有较高的预测精度和较好的泛化能力.

(3)由于BP是一种前向静态映射神经网络，在对与时间有关的年径流预测时效果往往不如Elman反馈动态递归网络.Elman是在BP神经网络的基础上，结构单元引入固定反馈环节，从而使系统具有适应时变特性的能力，使预测性能比BP网络更好，进而改善系统的动态性能.从本实例可以看出，Elman网络模型无论是拟合平均相对误差、拟合最大相对误差，还是预测平均相对误差、预测最大相对误差均优于BP网络模型.

3 结语

目前，将GA用于优化BP神经网络结构和参数的研究较多，但用于动态网络优化的研究较少.本文基于Elman神经网络基本原理，针对Elman神经网络采用BP算法进行权值修正时，同样存在着学习速度较慢，易陷入局部极小值等固有缺陷，提出一种基于GA优化Elman神经网络连接权值的GA-Elman多元变量年径流预测模型，以新疆伊犁河雅马渡站径流预测为例进行实例分析，结果表明GA-Elman模型用于多元变量年径流预测是合理可行的，模型具有较高的预测精度和较好的泛化能力.但由于GA算法在处理复杂优化问题上可能存在着早熟收敛、易陷入局部极值等缺点和不足，改进的GA算法，如多种群遗传算法、量子遗传算法和免疫遗传算法等可以有效避免其早熟收敛、易陷入局部极值等现象［17－18］，进一步提高Elman模型的预测精度和泛化能力.

［1］张楠，夏自强，江红.基于多因子量化指标的支持向量机径流预测［J］.水利学报，2010，41(11):1318-1323.(ZHANG Nan，XIA Zi-qiang，JIANG Hong.Prediction of runoff based on the multiple quantity index of SVM［J］.Journal of Hydraulic Engineering，2010，41(11):1318-1323.(in Chinese))

［2］谷晓平，王长耀，王汶，等.应用于水文预报的优化BP神经网络研究［J］.生态环境，2004，13(4):524-527.(GU Xiaoping，WANG Chang-yao，WANG Wen，et al.Research on the optimization neural network model for hydrologic forecast［J］.Ecology and Environment，2004，13(4):524-527.(in Chinese))

［3］庞博，郭生练，熊立华，等.改进的人工神经网络水文预报模型及应用［J］.武汉大学学报:工学版，2007，40(1):33-36.(PANG Bo，GUO Sheng-lian，XIONG Li-hua，et al.A modified artificial neural network model and its application to flood forecasting［J］.Journal of Wuhan University(Engineering Science)，2007，40(1):33-36.(in Chinese))

［4］蓝永超，康尔泗，徐中民，等.BP神经网络在径流长期预测中的应用［J］.中国沙漠，2001，21(1):97-100.(LAN Yong-chao，KANG Er-si，XU Zhong-min，et al.Long-term runoff forecasting with BP neural network model［J］.Desert in China，2001，21(1):97-100.(in Chinese))

［5］尹哗，梁川.改进的BP网络模型及其在日径流预测中的应用［J］.云南水力发电，2005，21(3):15-17.(YIN Ye，LIANG Chuan.Application of modified BP model to daily runoff forecasting［J］.Yunnan Water Power，2005，21(3):15-17.(in Chinese))

［6］邓霞，董晓华，薄会娟.基于BP网络的河道径流预报方法与应用［J］.人民长江，2010，41(2):56-59.(DENG Xia，DONG Xiao-hua，BO Hui-juan.River runoff forecasting method based on BP network and its application［J］.Yangtze River，2010，41(2):56-59.(in Chinese))

［7］傅荟璇，赵红.MATLAB神经网络应用设计［M］.北京:机械工业出版社，2009.(FU Hui-xuan，ZHAO Hong.Application of MATLAB neural network design［M］.Beijing:Mechanical Industry Press，2009.(in Chinese))

［8］丛爽.面向MATLAB工具箱的神经网络理论与应用［M］.合肥:中国科学技术大学出版社，2009.(CONG Shuang.Toolbox for MATLAB neural network theory and application［M］.Hefei:China University of Science and Technology Press，2009.(in Chinese))

［9］张德丰.MATLAB神经网络应用设计［M］.北京:机械工业出版社，2009.(ZHANG De-feng.MATLAB neural network design［M］.Beijing:Mechanical Industry Press，2009.(in Chinese))

［10］董长虹.Matlab神经网络与应用［M］.北京:国防工业出版社，2002.(DONG Chang-hong.Matlab neural network and application［M］.Beijing:National Defense Industry Press，2002.(in Chinese))

［11］刘永霞，冯仲科，杜鹏志.Elman动态递归神经网络在树木生长预测中的应用［J］.北京林业大学学报，2007，29(6):99-103.(LIU Yong-xia，FENG Zhong-ke，DU Peng-zhi.Application of Elman dynamic recurrent neural network to forecast tree growth［J］.Journal of Beijing Forestry University，2007，29(6):99-103.(in Chinese))

［12］符利勇，何铮，刘应安.基于改进Elman神经网络的林隙大小预测模型［J］.南京林业大学学报，2011，35(3):28-32.(FU Li-yong，HE Zheng，LIU Ying-an.Model based on modified Elman neural network for forecasting forest gap size［J］.Journal of Nanjing Forestry University，2011，35(3):28-32.(in Chinese))

［13］苑希民，李鸿雁，刘树坤，等.神经网络和遗传算法在水科学领域的应用［M］.北京:中国水利水电出版社，2002.(YUAN Xi-min，LI Hong-yan，LIU Shu-kun，et al.Neural networks and genetic algorithms in water science applications［M］.Beijing:China Water Power Press，2002.(in Chinese))

［14］汪金良，卢宏，曾青云.GA-BP算法及其在冰铜品位神经网络模型中的应用［J］.江西有色金属，2003，17(3):39-41.(WANG Jin-liang，LU Hong，ZENG Qing-yun.Application of GA-BP to the matte grade model based on neural network［J］.Jiangxi Nonferrous Metals，2003，17(3):39-41.(in Chinese))

［15］MATLAB中文论坛.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010.(MATLAB Chinese Forum.MATLAB neural network analysis of 30 cases［M］.Beijing:Beihang University Press，2010.(in Chinese))

［16］郭淳，李祚泳，党嫒.基于免疫进化算法的BP网络模型在径流预测中的应用［J］.水资源保护，2009，25(5):1-4.(GUO Chun，LI Zuo-yong，DANG Yuan.Runoff prediction application of BP neural network model based on immune evolutionary algorithm［J］.Water Resource Protection，2009，25(5):1-4.(in Chinese))

［17］史峰.MATLAB智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2011.(SHI Feng.MATLAB intelligent algorithm 30 case analysis［M］.Beijing:Beihang University Press，2011.(in Chinese))

［18］雷德明，严新平.多目标智能优化算法及其应用［M］.北京:科学出版社，2009.(LEI De-ming，YAN Xin-ping.Multiobjective intelligent optimization algorithm and its application［M］.Beijing:Science Press，2009.(in Chinese))