钢筋混凝土构件组合体徐变系数的计算

黄卫兰，陈灿明，陈 程，唐崇钊，陆道彪

(1.南京水利科学研究院 水利部水科学与水工程重点实验室，江苏 南京 210029;2.江苏省苏科建设技术发展有限公司，江苏 南京 210008)

承受长期荷载的钢筋混凝土构件，荷载不变时钢筋应力增加而混凝土应力减小，这种现象称混凝土徐变引起的构件应力重分布.由于钢筋对混凝土徐变的影响，钢筋混凝土构件的徐变变形将小于无配筋构件的变形.在混凝土变形特征及工作环境给定时，这种含筋构件的应力重分布及其变形特征主要与受力钢筋用量、布置及构件的受力状态有关［1－2］.

我国混凝土徐变研究最初有赖于大坝观测试验、大体积混凝土结构温度应力计算和钢筋混凝土构件预应力衰减估计等应力问题研究的开展，松驰系数成了徐变试验结果，应用于原观分析及温度应力的计算.变形控制是现代桥梁建设和大跨径钢筋混凝土桥梁营运管理的重要技术.轴压和弯曲是桥梁构件(塔柱、梁)的主要荷载变形，有关规范和以往研究［1，3］给出和讨论了钢筋用量对构件轴压变形的影响，没有涉及到布筋状况和弯曲变形下的取值问题，本研究认为由轴压修正的取值不能运用到弯曲变形的计算.

钢筋混凝土构件是非均质多连体，在计算结构或构件体系的长期变形时将其简化为单体，需要给出含筋混凝土的组合徐变系数.在确定构件的组合徐变特征如徐变系数、徐变度及弹性模量时，可以采用试验法、经验取值法、修正公式法等途径.试验法可以通过典型布筋方式、构件尺寸形状和荷载状态等条件的构件变形和应力测试，作为验证用.经验取值是一种笼统的取值法，运用时还有赖于工程师的经验与判断.根据构件配筋状况及受力状况的不同，采用修正公式确定配筋构件的组合徐变系数对于计算钢筋混凝土结构的长期变形具有重要的实用价值.

就计算分析而言，同一问题的计算结果及演算推导的繁简，会因采用的变荷载下混凝土徐变计算法，即徐变方程式的不同而有差异.其中最简单的有有效模量法和老化理论法(或流动率法);考虑应力减少时徐变部分可复的计算方法和具体形式较多［4］，弹性徐变理论(及类似的公式)在我国水利界是影响广、应用多的一种徐变计算法，该法可以考虑早龄期混凝土徐变部分不可复(晚期完全可复)，然而对本问题的推演计算却颇为繁难［5］，要应用数值解析法.本文以钢筋混凝土压柱和梁为例，探讨计算方法和构件承载形式对计算结果的影响，同时采用配筋压柱试件和纯混凝土压柱试件作徐变测试，将试验结果与计算结果作对比分析，提出较为简单而又接近实际的计算方法.

1 钢筋混凝土压柱的组合徐变系数

1.1 基本方程

以Eg，εg，σg表示钢筋(纵向)的弹性模量、应变及应力，以E，ε，σ表示混凝土的弹性模量、应变和应力.其中除Eg外，其他各变量均可视为时间的函数.P，ωg，ω，μ分别为钢筋混凝土压柱上的轴向荷载、钢筋和混凝土截面积及压柱配筋率.在线应力应变假设下，根据钢筋和混凝土的应变协调条件，有

有效模量法计算混凝土的应力应变，假定混凝土应力减小时徐变完全可复，将变形协调方程(1)变换成如下形式:

式中:φ为混凝土的徐变系数.

徐变曲线平行假说(老化理论)或流动假定，假设混凝土应力减少时徐变变形完全不可复，协调方程(1)可写成如下形式:

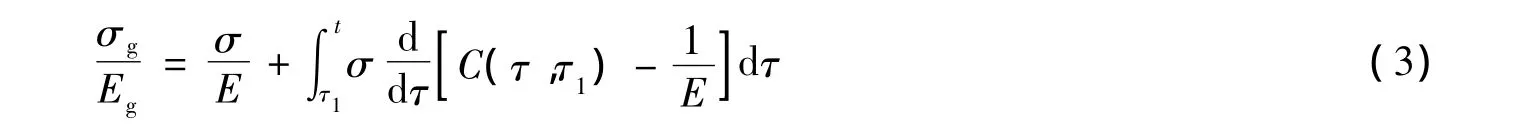
式中:C(τ，τ1)为混凝土徐变度，弹性模量E为时间变量E(t)或E(τ).

在计算钢筋混凝土构件变形及截面应力的重分布时，当混凝土应力减小，有效模量法假设徐变完全可复，老化理论假设徐变完全不可复，因此2种计算方法所得结果相差最大.本文主要讨论方程(2)和(3)两种形式的协调方程;作为比较，还推演讨论了考虑徐变部分可复的继效流动率法的近似结果.

钢筋混凝土组合柱的常荷载P由钢筋与混凝土共同承担，有荷载平衡方程如下

式中:μ=ωg/ω为截面配筋率.应用平衡方程(4)与变形协调方程(2)或(3)可以解出应力σg或σ.由于构件的变形与钢筋应力成比例，在解出应力σg及其初始值后，即可得到构件组合体的徐变系数φm:

1.2 按有效模量法求解方程

引入弹性模量比，并记以n=Eg/E(τ1)，将协调方程(2)写成如下形式

再将式(6)代入方程(4)，经移项整理，即可得到钢筋应力σg计算公式如下

式中:σ0为混凝土应力初始值;σ0=P/(ω(1+μn)).

因 φ≥0，μn＞0，故由式(8)可得 φm＜φ;又因 n＞1，由式(9)得 Em＞E.

1.3 按老化理论法求解方程

将方程(3)两边乘以Eg，再求导可得

改写平衡方程(4)为σ=P/ω-μσg，然后用σ及其一次微分代入式(10)，可得到求解σg的一次变系数非齐次微分方程

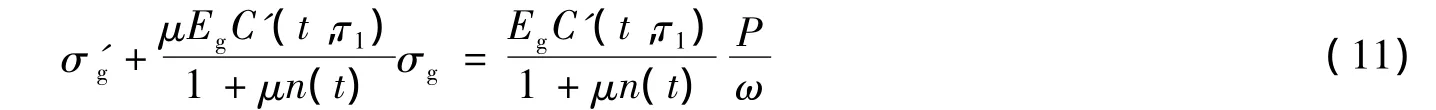
式(12)等号右边第1项nσ0为钢筋的初始弹性应力，第2项除以nσ0即为压柱的组合体徐变系数φm:

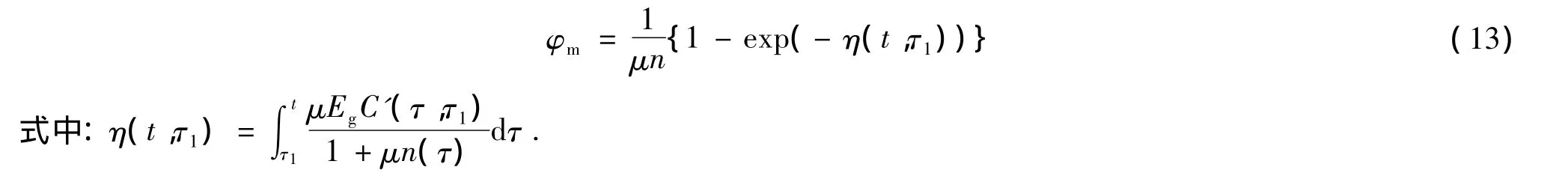
由于μn(t)值相对较小，桥用高性能混凝土早期强度和弹性模量都较高，3 d后的弹性模量增长趋于缓慢［6－9］.当 E(360)/E(3)的比值在1.3 ～1.4 范围以内时，可以采用下式计算 η(t，τ1):

1.4 徐变部分可复压柱综合徐变系数近似计算式

混凝土荷载应力减小或经历一段加载时间后卸载，徐变部分可复已为试验普遍证实.继效流动法［10］将徐变度C分为可复变形Cy(又称弹性后效)和不可复徐变Cn两部分，协调方程形式如下

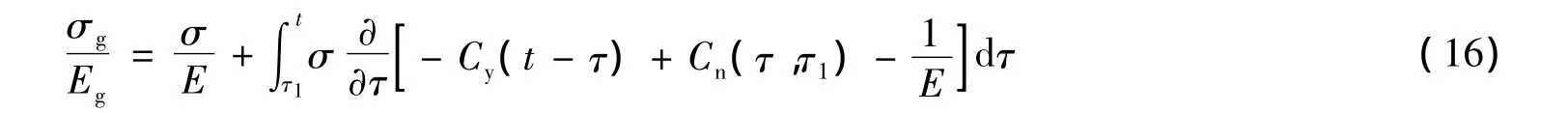
式中:可复变形Cy和徐变度可直接由试验给出，两者之差即为不可复徐变Cn.可复变形Cy与加载时的弹性瞬时变形相比一般在0.12～0.18范围内，卸载后48 h可以达到徐变稳定值的50% ～80%［8，11］.为简化推演计算，将这一变形归并入弹性变形而采用迟后模量Ey代替弹性模量E，钢筋混凝土压柱的变形协调方程可以写成如下形式

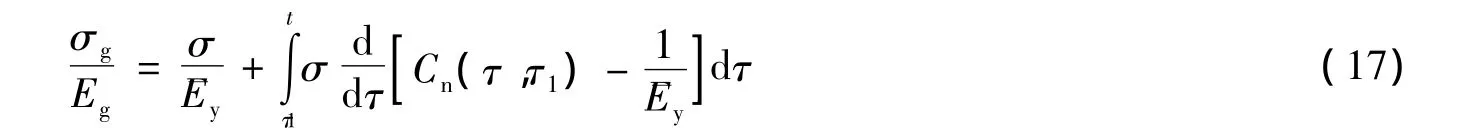
式中:迟后模量Ey=E/(1+ECy)=E(1+φy)，φy为可复徐变系数，其值为ECy.

上述方程(17)与老化理论法的协调方程(3)形式相同，可以与平衡方程(4)一起联合求解，结果如下

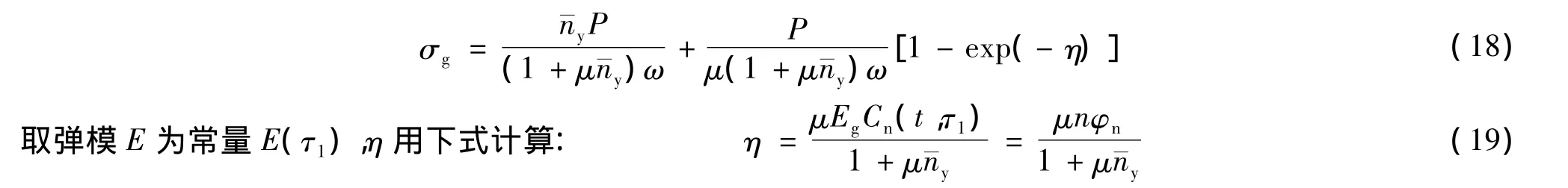
式中:φn为不可复徐变系数，其值为E(τ1)Cn.

将式(18)减去初始值nσ0，得到依时间增加的应力值Δσg如下

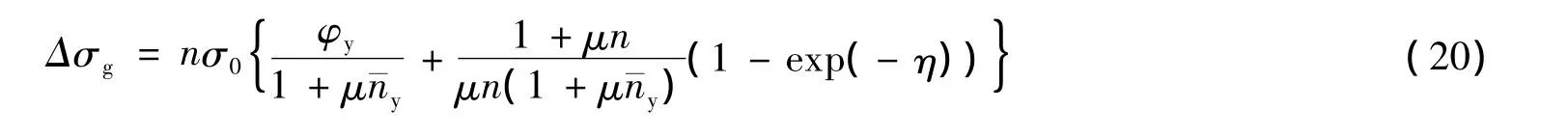
两边除以应力初值nσ0，再以可复变形系数φy(t)取代稳定值φy，可得压柱综合徐变系数φm如下

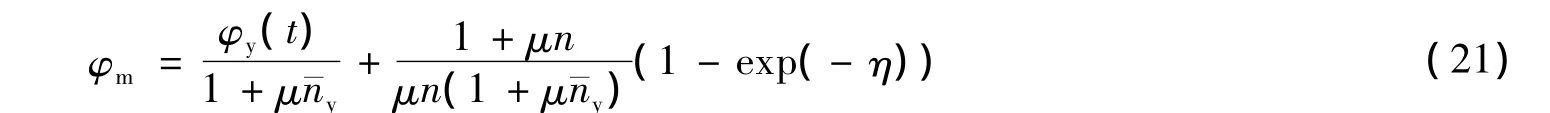
2 算例与试验验证

制作2组试件，混凝土强度等级C60，一组配置纵筋u为2%，另一组未配筋，试件为直径20 cm，高60 cm的圆柱体，内置标距25 cm的差动电阻应变计.配合比说明见表1，具体材料为:江苏巨龙水泥集团有限公司生产的巨龙牌P.Ⅱ52.5R水泥;南京热电厂Ⅰ级粉煤灰;宿迁洛马湖产的细骨料河砂;徐州睢宁产石灰岩碎石;UC－Ⅱ型高效减水剂;Ⅱ级钢.

表1 每立方米混凝土材料用量Tab.1 Material dosages per cubic meter of concrete

龄期7 d加载，测得的弹性模量及徐变系数，以及按上文计算的钢筋混凝土柱的组合弹模及徐变系数见表2［8］.计算时E及φ均用未配筋一组试件的相应值.

表2 试验测值及计算值比较Tab.2 Comparison between measured and calculated values

从表2可见，有效模量法与老化理论法的推算结果相差不大，继效流动法和老化理论法的结果与试验值更为接近.由于钢筋的截面刚度(Egωg)与截面混凝土刚度之比μn相对较小，钢筋对徐变的影响也小，这是3种徐变计算法结果相差较小且都与实际测值接近的主要原因;普遍的试验结果认为，徐变变形中可复部分所占比例较小，以不可复部分为主，这是表2中老化理论法较有效模量法结果更接近试验值的原因;由于继效流动法考虑了徐变的部分可复性，可复变形取用测试结果，其计算结果介于前两者之间并与实测值更接近，这是可以理解的.从计算结果的真实性及工作繁简看，3种徐变计算方法都可以接受.

3 钢筋混凝土受弯构件的组合徐变系数

钢筋混凝土矩形梁高h，宽b，上下2层布置非预应力钢筋，其中心距为h0，上、下层钢筋面积ωg;设混凝土拉压应力强度比均在线性变形范围内，且拉、压变形特征相同;徐变计算采用老化理论模型，截面变形采用平面假设.由以上假设，有变形协调方程如下

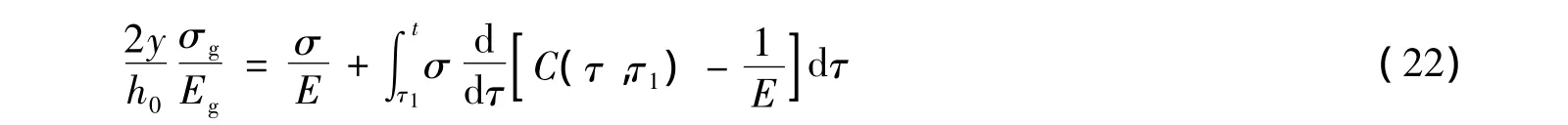
式中:y为截面应力计算点距中和轴的距离;σ为混凝土应力，为时间t和坐标y的变量.

上式等号两边乘以h0Eg/2，再对时间t求导，得到微分方程

式中:φ为混凝土的徐变系数φ =C(t，τ1)·E(τ1).

方程两边乘以y，并积分，因σ'g与坐标y无关，故有

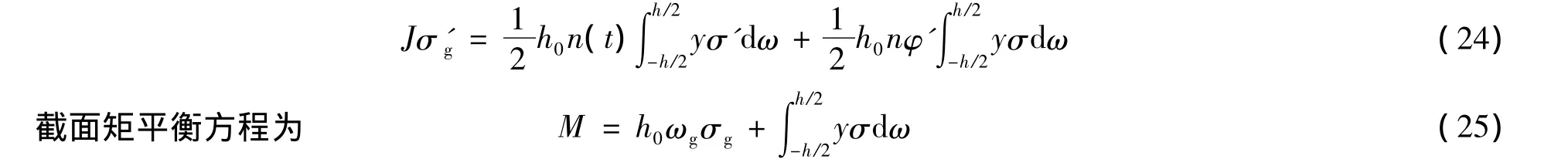
然后用方程(25)及其时间微分式将方程(24)中含σ及σ'的积分项消去，经整理移项得到微分方程和初始条件如下

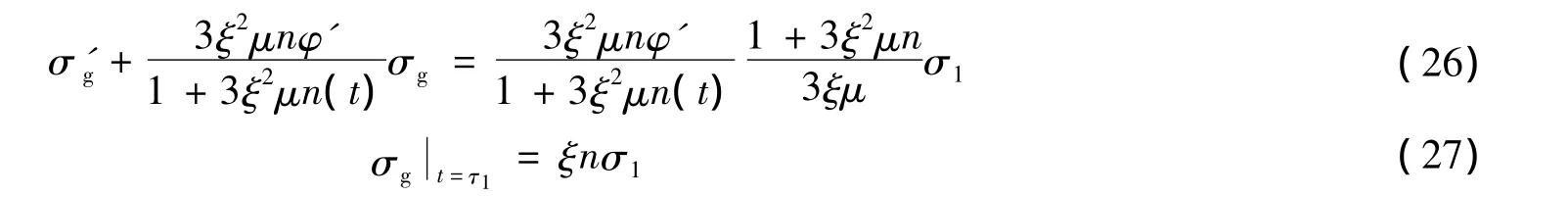
式中:σ1为截面边缘的混凝土应力(极值)满足方程(26)及初始值条件(27)的解为

式中:n(x)可用n或采用28 d的弹性模量计算，即用Eg/E(28).计算结果见表3.

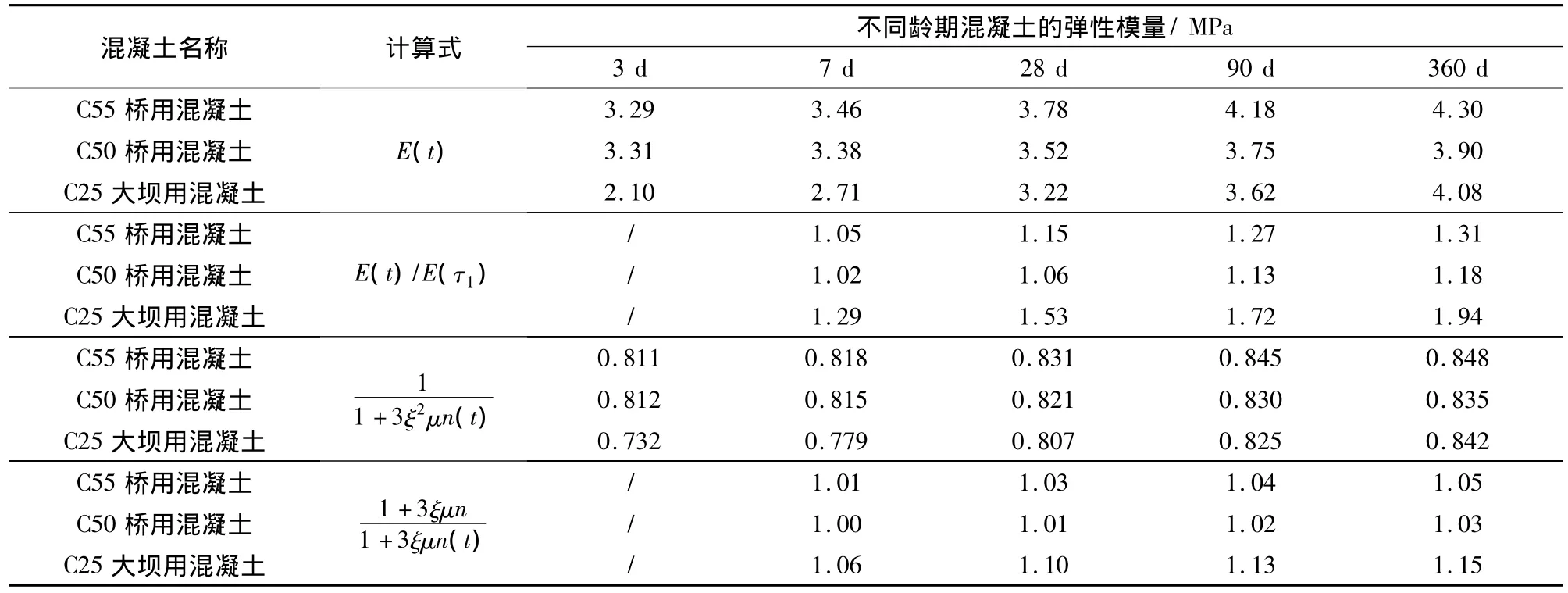
表3 混凝土弹性模量变化与1/［1+3ξ2μn(t)］变化Tab.3 Changes in concrete elasticity modulus and 1/［1+3ξ2μn(t)］

从表3可见，混凝土360 d或最终的弹性模量与初始加载时的相比在20%以内增加时，可不考虑其变化并采用n(x)=n;当其在20% ～40%增加时，可用28 d弹性模量计算，n(x)=Eg/E(28).

设由前面算例中的钢筋混凝土柱受偏心荷载作用产生压弯变形，现计算弯曲徐变系数φm与压缩徐变系数进行比较，结果见表4.计算时，取 n=n(x)=Eg/E(τ1)，ξ=0.9，μ =0.02.

表4 混凝土与构件压、弯徐变系数比较Tab.4 Comparison between concrete and members compression and bending creep coefficients

从表4可见，虽然截面上配筋率相同，钢筋混凝土压柱截面混凝土应力均匀分布，而受弯构件混凝土应力非均匀分布且钢筋集中在应力较大的区域(上、下层)，弯曲状态下钢筋对徐变的阻滞作用要大于轴向压缩状态，混凝土弹性模量变化的影响也比前者要大;就本算例而言，取用轴压徐变系数代表弯曲徐变系数，偏差值达到18%以上.

4 结语

计算钢筋混凝土构件组合体的徐变系数及弹性模量时，徐变方程采用有效模量法方程和老化理论法方程较为简单，计算结果也相差不大.

根据压柱3种徐变计算法结果与试验结果的对比，说明有效模量法方程推演计算最为简单;采用老化理论法方程时，计算结果比前者接近实际，需要求解一次微分方程但能给出封闭解;继效流动法的计算值则介于以上两者之间，最接近试验值.受弯构件截面应力为非均匀分布，钢筋主要集中在截面应力较高的部分，钢筋对混凝土徐变的阻碍效应增强.当钢筋混凝土构件以压弯荷载为主时，应同时给出这2种荷载状态的徐变特征.

［1］苏清洪.加筋混凝土收缩徐变的试验研究［J］.桥梁建设，1994(4):11-18.(SU Qing-hong.Test study on the shrinkage and creep of reinforced concrete［J］.Bridge Construction，1994(4):11-18.(in Chinese))

［2］徐锋，庞建栋.混凝土的弯曲变形和损伤研究［J］.公路工程，2007(4):107-109.(XU Feng，PANG Jian-dong.Research on deformation and damage of bending concrete［J］.Highway Engineering，2007(4):107-109.(in Chinese))

［3］周履，陈永春.收缩徐变［M］.北京:中国铁道出版社，1994:328-350.(ZHOU Lv，CHEN Yong-chun.Concrete shrinkage and creep［M］.Beijing:China Railway Publishing House，1994:328-350.(in Chinese))

［4］惠荣炎，黄国兴，易冰若.混凝土的徐变［M］.北京:中国铁道出版社，1988:64-66.(HUI Rong-yan，HUANG Guo-xing，YI Bing-ruo.Concrete creep［M］.Beijing:China Railway Publishing House，1988:64-66.(in Chinese))

［5］阿鲁久涅扬Н Х.蠕变理论中的若干问题［M］.北京:科学出版社，1961.(ARUTJUNJAN H X.Some problems in theory of creep［M］.Beijing:Science Publishing House，1961.(in Chinese))

［6］陈灿明，黄卫兰，唐崇钊，等.混凝土强度与弹模依时增长相关性公式的试验研究［J］.公路工程，2010(1):51-55.(CHEN Can-ming，HUANG Wei-lan，TANG Chong-zhao，et al.Experimental study on the formula of the relevance between concrete strength and elasticity modulus［J］.Highway Engineering，2010(1):51-55.(in Chinese))

［7］陈灿明，黄卫兰，王宏，等.大跨径桥梁高强混凝土收缩徐变特性研究［J］.水利水运工程学报，2010(4):62-67.(CHEN Can-ming，HUANG Wei-lan，WANG Hong，et al.A study of high-strength concrete creep and shrinkage for long-span bridges［J］.Hydro-Science and Engineering，2010(4):62-67.(in Chinese))

［8］陆采荣，王永安，姜竹生，等.大跨度超宽幅桥梁高性能混凝土研究与应用报告［R］.南京:南京水利科学研究院，2006.(LU Cai-rong，WANG Yong-an，JIANG Zhu-sheng，et al.Research and application report of high-performance concrete for long-span and ultra-wide bridge［R］.Nanjing:Nanjing Hydraulic Research Institute，2006.(in Chinese))

［9］陈灿明，黄卫兰，陆采荣，等.桥用高性能混凝土的徐变与应用［J］.水利水运工程学报，2007(2):1-9.(CHEN Canming，HUANG Wei-lan，LU Cai-rong，et al.Creep of high-performance concrete for bridges and its application［J］.Hydro-Science and Engineering，2007(2):1-9.(in Chinese))

［10］唐崇钊.混凝土的徐变力学与试验技术［M］.北京:水利电力出版社，1982:203-204.(TANG Chong-zhao.Concrete creep mechanics and test technology［M］.Beijing:Water Resources and Electric Power Press，1982:203-204.(in Chinese))

［11］陈灿明，黄卫兰，唐崇钊，等.大跨径预应力混凝土桥梁高强度混凝土材料特性研究总报告［R］.南京:南京水利科学研究院，2010.(CHEN Can-ming，HUANG Wei-lan，TANG Chong-zhao，et al.General research report of high-strength concrete material characteristics for long-span pre-stressed concrete beam bridges［R］.Nanjing:Nanjing Hydraulic Research Institute，2010.(in Chinese))