结合稀疏逼近的正则化方法求解非齐次双调和方程的Cauchy问题
2013-11-15刘晓宇
◆刘晓宇
(重庆工商大学融智学院)
一、引言
二维双调和方程在很多实际问题中需要用到。但是实际的工程应用中,已知的边界条件可能不完整或者不准确,这样的问题就是反问题,一般来说反问题是不适定的。本文研究的Cauchy问题就是一种反问题,因而在求解过程中,用基本解方法得到的最小二乘问题的解是不唯一的,需要通过使用正则化方法提高原问题数值求解的准确度。
用基本解方法求解齐次双调和方程会导致离散的Cauchy问题的线性方程不是满秩的或是超定的,其解的适定性存在问题,故本文将使用稀疏逼近的正则化方法来求解离散方程组,以避免直接求解非齐次方程时会出现的不确定性。
传统的Tikhonov正则化方法是将线性反问题

重新表示为
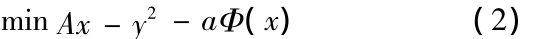
并选择二次罚项,以使得近似解具有光滑性。本文选择的稀疏逼近正则化方法,即Φ(x)=x1,同时借助稀疏逼近的优势,在减少结点数目的同时,仍得到较好的结果。
本文还考虑到给定的边界数据有扰动,即有噪声的情况下的数值方法的稳定性。
二、问题的数学表述
二维开区域Ω∈R2上的非齐次双调和写为:

或表示成两个Possion方程:


若该问题有解,则在求解过程中会出现病态的线性方程组,方程组不满秩或者是超定的且条件数很大。本文使用结合稀疏逼近的正则化方法的边界结点法求解满足边界条件(5)的双调和方程(3)或(4)。
三、结合稀疏逼近正则化方法的边界结点法
方程(3)的解可以写为:

up(Χ)和uh(Χ)分别是方程的特解和通解。up(Χ)满足

但是,它不一定满足边界条件。而通解uh(Χ)满足:

以及边界条件(5)
(一)求非齐次双调和方程的特解
边界结点法中,非齐次方程(5)的特解近似表示为[3]:

(二)求非齐次双调和方程的通解
本文用Laplace方程的基本解和双调和方程的基本解的线性组合来近似表示非齐次双调和方程的通解。Laplace方程的基本解是G1(X,Y),双
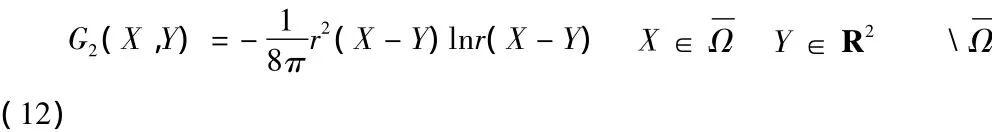
则齐次方程(8)的解uh(Χ)由基本解的线性组合近似表示。

其中,L是源点数,{ cj}和 { dj}是待定系数,{ Yj}是源点,X是边界点。uh(Χ)满足给定边界条件(9),(10)[3]。为求解待定系数,在已知边界条件的部分边界 Γ1上选取 n个结点 Xi,当 X=Xi,(i=1,2,...,n)时,我们得到uh(Χ)所满足的边界条件构成的方程组Aλ=b,这个方程组的系数矩阵一般不是方阵,因此将求解该线性方程组转化为如下极小值问题:

其中,||·|| 是2- 范数,λ =(c1,c2,...,cL,d1,d2,...,dL)Τ是待定系数向量。系数矩阵A和已知的边界条件向量b分别为:
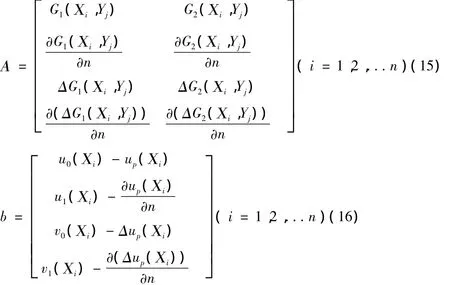
由于本文研究的问题是不适定的,为了得到较为准确的结果,本文使用稀疏逼近方法结合最小二乘方法来求解极值问题(14)。
由于测量只能得到近似的边界条件,故在给定的边界数据有噪声的情况下求解极值问题(14)变为求解如下的最小二乘问题

(三)稀疏逼近正则化
最小二乘问题(14)中的系数矩阵A是4n×2L矩阵。为得到最小二乘问题的解,假设4n≥2L。本文问题转变为如下形式:

这里,T是一个正实数。利用[1]中所提到lasso算法,其全称是leastabsoluteshrinkageandselectionoperator。其想法可以用如下的最优化问题来表述:
在限制了mλinλ1的情况下,求使得残差平方和
b-Aλ22达到最小的回归系数的估值。
lasso算法的步骤如下[6]:
μ——当前最小角度方向,即角平分线方向y^——当前拟合的y值

当边界数据有噪声作用时,边界条件向量b变为b,且设b=b(1+e%),此时同样用上述算法可以求出待定系数,并得到最后的近似解。
四、数值算例
本节算例验证第2、3节所分析的边界结点法,以及它应用于求解非齐次双调和方程Cauchy问题的有效性和结果关于数据噪声的稳定性。本文定义u(an)i和ui分别为未知边界上第i(i=1,2,...,n)个结点处的精确解和数值解。

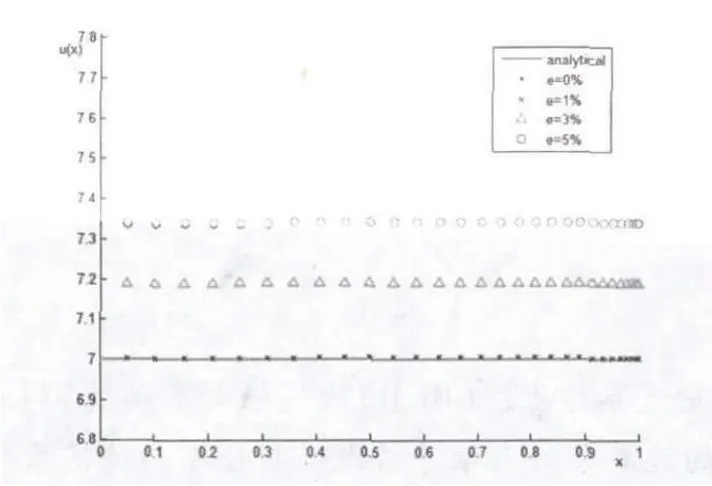
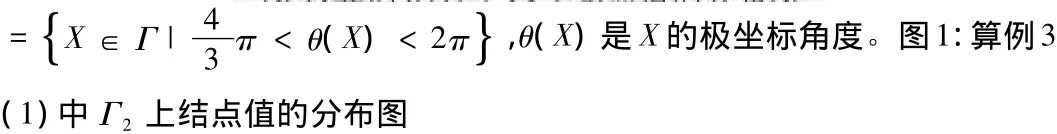
图1:在噪度e分别为e=0% ,e=1% ,e=3% 和e=5% 时Γ2上结点处的u(X),结点个数为n=30。该图表明计算结果与精确解是吻合的,且随噪声的减小呈收敛趋势。
五、总结
本文使用稀疏逼近正则化方法结合边界结点法求解非齐次双调和方程的Cauchy问题,从数值试验的结果可以看出,这是可行的。并且从以上算例中可以看出,在对源点数、结点数和内点数的关系,以及源点到边界的距离作[3]中的要求的情况下,计算结果与[3]类似,但是精度更高。结果是较准确的,且在该范围内,误差非常小,即使所取点数较多,计算时间仍然较少。当边界条件有较小噪声时,计算结果仍然是稳定的,且随噪声的减小而收敛。
[1]Stephen J.Wright,Robert D,Sparse Reconstruction by Separable Approximation,IEEE Transactions on Signal Processing,2009.2479.
[2]祝家麟.边界元分析.科学出版社,2009.
[3]刘晓宇,王小军,杜亚楠.用边界结点法(BKM)求解非齐次双调和方程的 Cauchy问题,2009,(11):154-166.
[4]W.Chen and M.Tanaka,New Insights in Boundary-only and Domain-type RBF Methods,Int J Nonlinear Sci Numer Simul,2000,1(3):145-52.
[5]Xiaolin Li and Jialin Zhu,The method of fundamental solutions for nonlinear elliptic problems,Engineering Analysis with Boundary Elements,2008,(10):1016.
[6]Robert Tibshirani.Regression shrinkage and selection via the lasso,Journal Royal Statostical Society B,1996(58):267-288.
