改进滑模变结构永磁电机控制器研发

张自友，周大鹏

（乐山师范学院物理与电子工程学院，四川 乐山 614004）

0 引 言

永磁同步电机（permanent magnet synchronous motor，PMSM）是一个强耦合、非线性的系统，具有体积小、噪音小、转动惯量小、功率密度高以及控制性能好等优点，目前已广泛应用于数控机床、机器人航空等领域[1]。

为实现对PMSM的优良控制并保持稳定性，需要获得转子的准确位置信息，而传统PMSM采用DTC直接转矩控制系统，使用机械式位置传感器既降低系统可靠性又增加了硬件成本[2]，因此，研究PMSM的无传感器控制成为了PMSM的热点问题[3]。

目前对PMSM进行无传感器控制的主要工作有：采用空间凸级效应的PMSM控制方法能应用于各种速度和取得较好的估算效果，但具有高频噪声的缺陷[4]；采用状态观测器通过电机反电动势提取位置信息的方法具有良好的动态特性，但不能对低速运转时的转子位置进行估计，因此，仅适用于中高速的转子位置估计[5]。

滑模变结构控制器具有结构简单和能适应各种速度宽度的优点，采用其设计的无传感器PMSM控制器主要工作有：文献[6]将径向神经网络RBF融入滑模控制器中，设计了以切换函数作为网络输入，以滑模控制器作为网络输出的神经滑模控制器。文献[7]设计了一种基于T-S模型和滑模控制器的模糊滑模控制器，通过自适应技术对范数进行估计，通过T-S模糊局部补偿器和滑模控制器构成全局控制器，使得全局闭环系统具有良好的跟踪性能和鲁棒性。文献[8]设计了基于空间矢量脉冲调制技术的系统，采用PI控制器调节磁链，通过转矩对电机空间矢量进行解耦，并通过转子位置和定子电流对定子磁链进行估算。本文在上述工作的基础上，提出了基于改进的滑模观测器的PMSM控制器设计方法，并通过实验证明方法的可行性。

1 PMSM数学模型

PMSM定子三相对称绕组如图1所示。

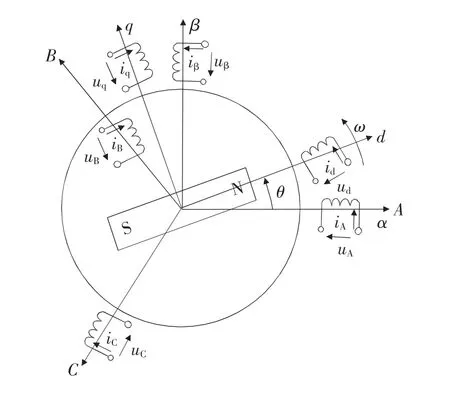
图1 PMSM定子三相对称绕组

根据基波合成磁动势在坐标变换前后的等效原则，可以将PMSM在三相静止坐标系A、B和C的数学模型变换到静止的αβ坐标系下，对应的数学模型如式（1）所示：

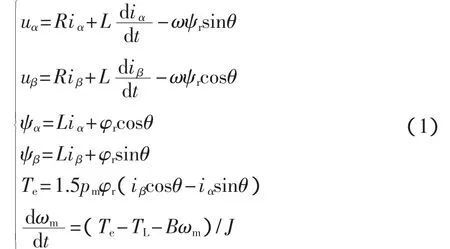
式中：L——α、β轴电压电感；

uα，uβ——α、β 轴电压；

iα，iβ——α、β 轴电流；

θ——转子位置；

φr——转子磁链；

ω，ωm——转子电角速度和机械角速度；

pm——极对数；

Te，TL——电磁转矩和负载转矩；

R——定子绕组电阻；

B——摩擦系数；

J——转动惯量。

2 传统滑模变结构观测器

滑模变结构控制器在运行过程中对开关函数sgn的符号进行判断，不断切换控制量来改变系统结构，并使得系统最终运动到切换面S=0上。

传统的PMSM滑模变结构观测器是通过对定子电流进行估计，然后与实际电流进行比较，最后通过两者的误差切换控制量实现控制，所以基于式（1），可以得到传统的滑模变结构观测器[3]：

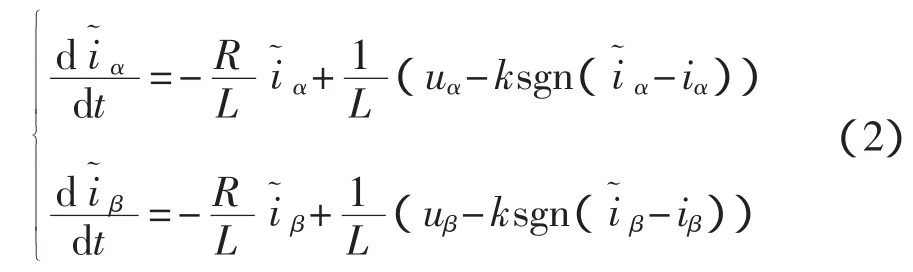
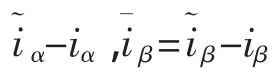
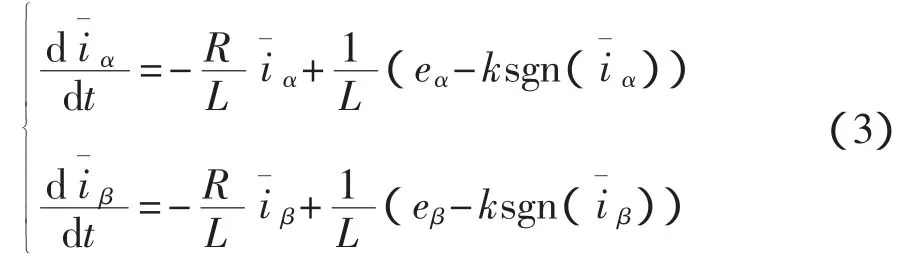
式中：k——滑模系数；

sgn（X）——开关函数，可以表示为

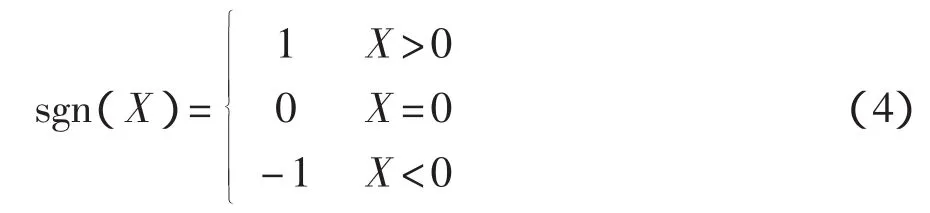
根据式（5）可以得到转子角度估算值：

由于传统滑模观察器中采用sgn（X）为高频开关信号，当在滑模面上进行滑模运动时，因开关空间和时间上的滞后，使得滑模观测器出现了抖振现象，影响了转子位置估算的准确性。

3 新型滑模变结构观测器

3.1 低通滤波

传统的滑模观测器会出现抖振现象，因此，在传统滑模观测器的基础上加入低通滤波器以消除抖振，如图2所示。

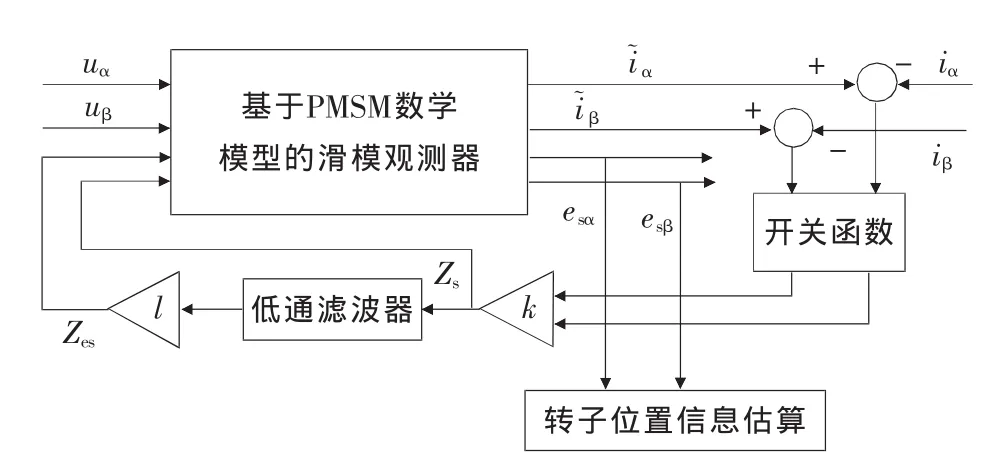
图2 带低通滤波器的滑模观测器

ωth——低通滤波器的截止频率。

将式（7）中的两式相互除，可得PMSM的转子转角和转速估计值：

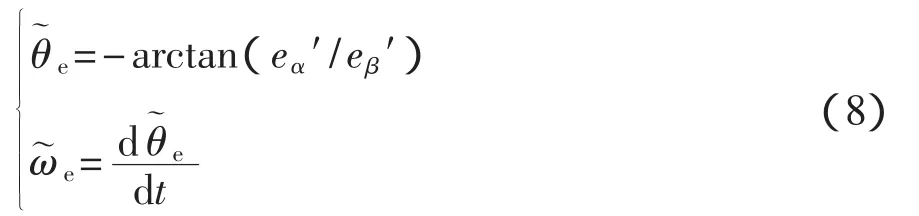
3.2 转角相位补偿

由于通过低通滤波得到的反电动势估算转子位置会出现偏差，使得相位滞后并随转子转速的增加滞后程度加剧，所以，将滑模观测器在图2的基础上进行改进，如图3所示。增加了相位补偿Δθ，加入相位补偿后的滑模观测器得到转角估计值可以表示为

3.3 抖动消除

滑模运动时会产生高频抖动，高频抖动不仅会影响控制精度，甚至会使得系统振荡失稳，因此，将准滑动模态控制思想加入到滑模观测器中，即将系统运行轨迹限制在某一邻域内，采用饱和函数取代开关函数，使得在边界层内进行连续控制而在边界层外切换控制以消除滑模抖振带来的影响。

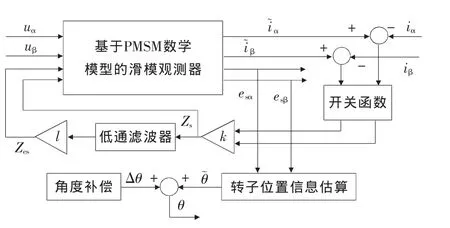
图3 带相位补偿的滑模观测器

饱和函数为

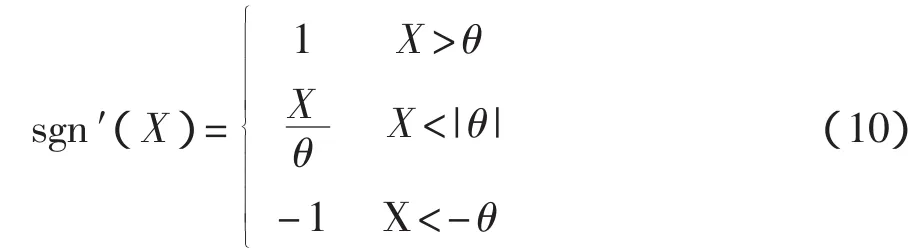
其中，θ为边界层厚度，θ值的设置需要通过系统反复测试获得，θ值过小会使得控制量过大，不能有效消除抖振；θ值过大，在消除抖动的同时却使得系统稳定性和鲁棒性降低。

采用饱和函数的滑模观测器如图4所示。

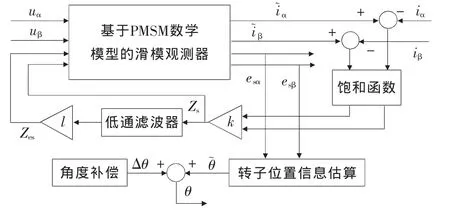
图4 加入饱和函数的滑模观测器

则改进的滑模观测器可以表示为

3.4 稳定性验证

将其对时间进行微分，可以得到：

若式（13）小于 0，则式（11）所示的滑模观测器是稳定的，此时有：

将式（11）代入式（14）可得：

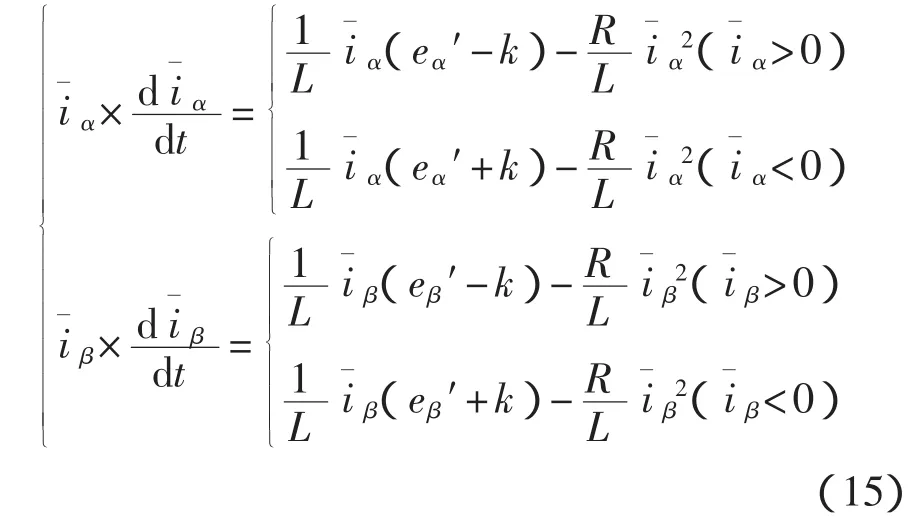
4 系统测试

采用Simulink对其进行仿真与测试。初始化时实验的具体参数：定子绕阻为0.5 Ω，定子相电感为9.5mH，定子相绕线自互感为4.5mH，转动惯量为4.12 kg·m2，最大转矩电流为10A，额定功率为0.8kW，额定转速为2500r·min-1，低通滤波器的截止频率为2MHz，参数k为1.25，边界层厚度为20。

图5和图6展示了测量转速与估算转速、测量转子位置和估计转子位置随时间变化的仿真曲线。可以看出本方法能较好地追踪实际转速和位置，具有较高的估算精度。在0.12s前，转子的估算转速有较小误差，在0.12s后，估算转速和实际转速基本拟合，几乎无误差；同时可以看出转子位置的估计值与测量值在仿真期间基本完全一致，具有较高的估算精度。

5 结束语

本文提出了一种基于改进滑模观测器的永磁同步电机无传感器控制方法，首先建立了永磁电机的数学模型，在此基础上建立了以电流误差为滑模面的滑模变结构观测器，为了提高估算的精度和减少滑模运动中的高频抖振，采用低通滤波对电流误差开关信号进行滤波，并采用饱和函数取代开关函数，从而对切换函数进行了改进，通过李亚普若夫稳态判断法验证其稳定性。仿真实验证明，本方法能较为准确地对转速和转子位置进行估算，是一种对PMSM进行无传感器控制的有效方式。

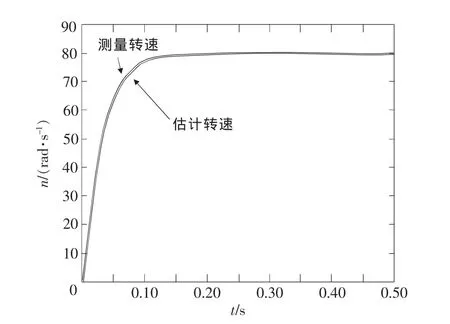
图5 转速仿真曲线

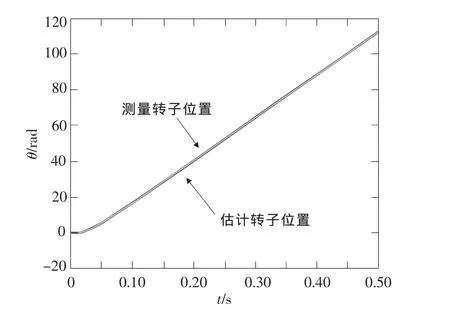
图6 转子位置仿真曲线

[1]王成元，夏加宽，杨俊友，等.电机现代控制技术[M].北京：机械工业出版社，2006.

[2]Sun D，Zhu J G，He Y K.A space vector modulation direct torque control for permanent magnet synchronous motor drive[J].IEEETransaction on Industry Applications，2003，39（6）：602－605.

[3]胡跃明.变结构控制理论与应用[M].北京：科学出版社，2003：74-84.

[4]赵德宗，张承进，郝兰英.一种无速度传感器感应电机鲁棒滑模控制策略[J].中国电机工程学报，2006，26（22）：122-127.

[5]Lu W Q，Hu Y W，Huang W X.A hybrid approach of sensorless rotor position self-sensing for brushless DC motor[C]//InternationalConference on Electrical Machines and Systems.Wuhan：IEEE，2008：1334-1337.

[6]王武，白政民，姚宁.永磁直线同步电机神经滑模控制仿真[J].电机与控制应用，2011，38（2）：22-25.

[7]张细致，王耀南，袁小芳.永磁同步电机自适应模糊滑模变结构控制[J].中国机械工程，2010，21（2）：206-211.

[8]徐振宇，黄守道，黄科元，等.基于滑模变结构的PMSM直接转矩控制[J].微特电机，2011，10（6）：44-47.