波浪作用下填筑式进海路基于ADINA的有限元分析
2013-11-12王桂兰史宏达潘新颖
王桂兰,史宏达,潘新颖,李 霈
(中国海洋大学 工程学院,山东 青岛 266100)
中国北方的滩浅海区域存在一定数量的油气资源,对于这一区域的油气资源的开发通常采用“海油陆采”的方式,先在滩浅海建设进海路和海上人工岛,然后在海上人工岛上建设采油井场,采用陆地上的开采工艺来开采海上油气资源[1]。目前,进海路结构主要有填筑式、高架桥式和隧道式三种形式[2-3],其中填筑式进海路因其结构简单、施工方便等优点而得到广泛应用,但填筑式进海路的边坡块体在恶劣海况的作用下,经常受到破坏,造成较大的经济损失。因此,本文应用非线性有限元分析软件ADINA,采用流固耦合的计算方法,对填筑式进海路在波浪作用下的受力情况进行有限元分析。进海路模型两侧护坡采用单一坡面和复式坡面两种型式,护坡分为整体式、大块石护面和小块石护面三种型式,分别进行数值模型计算,分析不同型式的受力和变形,找出结构中受力较大的薄弱位置,建议在薄弱位置增大块体重量,以提高结构的安全性,减小破坏。
1 数学模型
1.1 波浪控制方程
对于二维不可压缩粘性流体的自由表面流动问题,整个流场以连续性方程和简化的N-S方程为控制方程[4-5]。连续方程和动量方程分别为
(1)
(2)
(3)
式中,ρ为密度;t为时间;u,v分别为流体y,z方向的速度分量;μ为动力学黏性系数;g为重力加速度。
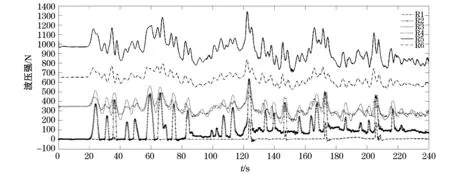
为了追踪自由液面的波动,采用VOF方法[6],在包含水与空气的平面网格单元中引入体积分数qw,其中qw=0表示单元内没有第w相流体,qw=1表示单元内全部为第w相流体,0 (4) (5) 数值造波采用给定流速和波高设置的造波边界法,以此产生一系列规则波。为了同时计算单一坡面与复式坡面的进海路并进行对比,本文采用的数值波浪水槽边界条件示意图如图1所示。图中阴影部分代表水,上部是空气。 图1数值波浪水槽边界条件Fig.1The boundary conditions of the numerical wave tank 模型边界条件设置如下:左右边界均设置为速度造波入射边界;顶部为大气,设置其边界上的单元q1=1,代表此处为空气边界条件;底边界为海底,通过施加固壁(wall)边界实现,虽然是粘性流体,但与海底的作用层相对于求解域来说可忽略,所以选择滑移固壁条件(slip wall),物理意义为速度矢量的法向分量为零,切向分量作为控制方程的未知变量计算;水槽模型中部与进海路结构模型接触边界设置为流固耦合FSI边界,具体见第2节。 选取某实际工程项目的进海路作为研究对象,共研究了整体式、大块石护面和小块石护面三种型式的进海路,以及单一坡面与复式坡面的进海路分别在设计高水位情况下受波浪作用的情况。进海路截面尺寸见图2。将整体式进海路左侧护面形式简化成一块大石块、七块小石块护面型式,3种护面型式的进海路结构网格图见图3。 图2 进海路尺寸Fig.2 The size of the filling-type sea road 图3 三种进海路结构网格图Fig.3 The mesh plots of three types of filling-type sea road structures 应用在流固耦合界面的基本条件是运动学条件df=ds和动力学条件n·τf=n·τs,其中df和ds分别表示流体和结构的位移,τf和τs分别为流体和结构的应力,n为流固耦合界面的外法线方向[7-8]。 流体和结构的模型是按照下面的方法耦合的:流固耦合界面上流体节点的位置是由运动学条件决定的。其他节点的位移由程序自动确定以保留初始网格的质量。另一方面,根据动力学条件,在流固耦合界面上,流体的分布力F(t)根据式(6)积分为集中力施加到结构节点上。 τf·dS (6) 式中,hd是结构节点的位移;S为流固耦合界面的面积。 耦合系统的解向量X记为X=(Xf,Xs),Xf,Xs分别是定义在流体和结构上的解向量。因此,ds=ds(Xs),τf=τf(Xf)。流固耦合系统F[X]的有限元方程可以表示为 (7) 式中,Ff和Fs分别是流体和结构的方程,可以分别表示为Ff[Xf,0]和Fs[Xs,0]=0。 本文采用迭代耦合求解方法,即流体方程和结构方程按顺序相互迭代求解,各自在每一步得到的结果提供给另一部分使用,直到耦合系统的解达到收敛,迭代停止;否则,需要重新解流体方程、结构方程、收敛检查。 本文计算波浪水槽总长度为218 m,水深2 m,左右水槽长度均设定为100 m,两侧波浪条件一致。中间部位为进海路模型。水槽尺寸见图4所示。 图4数值波浪水槽尺寸Fig.4 The size of numerical wave tank 在两侧造波边界加载海浪谱的时程入口速度条件,拟模拟波高1.0 m、周期4.0 s的波浪,对设计高水位进海路前水深为2 m的整体式、大块石护面和小块石护面三种型式及单一坡面与复式坡面两种断面的进海路在该工况下进行数值模拟。 如上所述,本文设计不同护面型式的3种断面,并且通过数值试验,得到了不同型式的进海路在波浪作用下的位移、应力应变结果,同时得到了在不同护面型式下进海路左右坡面共11个测点的水平波压强,如图5所示。对进海路左侧单一坡面等间距取5个测点,对进海路右侧复式坡面上下坡等间距取6个测点,总计11个测点。 图5 进海路左右两侧测点编号Fig.5 The numbering of the measuring points along the two sides(left and right) of the filling-type sea road 3个模型出现最大y向水平位移时的位移如图6所示。由整体斜坡式进海路可知,左侧单一坡面胸腔部位的位移值较右侧复式坡面的位移值大了25%左右,说明复式坡面对进海路整体起到较好的消浪作用。 同时,从3种结构整体位移变化可知,小块石护面的进海路水平位移最大,其最大值约为9 mm,出现在底部护面块石与进海路堤心接触的地方,方向背离进海路。说明此处护面块石受波浪作用易向海方向运动;其次是大块石护面的进海路,进海路堤心位移几乎为零,护面大块石的位移从上到下逐渐减小,这主要是因为大块石上部处于静水面附近,受波浪波峰和波谷交替作用最强。 在波浪作用下,整体进海路内部产生应力应变。3种结构型式的进海路所受的最大应力如图7所示。 比较这3组应力分布图,可以发现进海路结构受力共性:进海路静水面附近上下各约半个波高处及堤脚附近的应力最大,判断其受波浪作用影响最大,若此处有护面块体,则最容易失稳,或被波浪冲击爬升过程中打翻,或在波浪回落过程中由于压差被波浪带走。同时也注意到进海路右侧复式坡面肩台折角处出现应力集中现象,主要是由于波浪由肩台爬坡后在此折角处出现聚集,波浪作用力相对较大。 图6 三种进海路的最大水平位移分布图Fig.6 The maximal y-displacement diagram of three types of filling-type sea roads 图7 三种进海路最大拉应力与最大压应力分布图Fig.7 The distributions of the maximal tensile stress and the compressive stress ofthree types of filling-type sea roads 3种结构型式的进海路产生的最大应变见图8。将这3组应变云图分别与图7的应力分布图进行对比,发现在进海路产生最大应力的地方或附近产生最大应变,结构应变分布与应力分布规律一致,不再赘述。 图8 三种进海路最大拉应变与最大压应变分布图Fig.8 The distributions of the maximal tensile strain and the compressive strain ofthree types of filling-type sea roads 根据进海路左右两侧节点所受的波压强大小,分析结构的受力情况,以整体式斜坡进海路为例,规定波浪水平正向冲击进海路为正方向。 结构左侧坡面5个测点波压强随时间变化情况如图9所示。左侧4号测点位于静水面以下约1/4波高处,在200 s时所受的波压强最大,约为1 400 N。这主要是由于波浪在该处爬升回落反复交替冲击。 图9 整体斜坡式堆石进海路左侧测点波压强时程变化Fig.9 The time-history curves of wave pressure at the measuring points on the left side ofthe whole slope filling-type sea road 进海路右侧6个测点的波压强随时间变化情况如图10所示。进海路右侧节点受波浪冲击规律与左侧节点大致相同。右侧5号测点在125 s时所受的波压强最大,约为1 300 N。其位于肩台坡面中部,说明此处受波压强冲刷比较严重。 图10 整体斜坡式堆石进海路右测点波压强时程变化Fig.10 The time-history curves of wave pressure at the measuring points onthe right side of the whole slope filling-type sea road 为分析不同断面进海路的受力情况,取复式坡面上部坡面与对应右侧单一坡面上部坡面所受的波压强合力大小时程变化如图11所示。从图中可以看出,右侧复式坡面上部坡面所受波浪冲击力合力整体均小于左侧单一坡面,这主要是由于复式坡面的肩台部分相对单一坡面起到了较好的消浪作用,故实际工程设计中,在波浪较大的海区推荐使用合适的复式坡面。 图11 整体式进海路左右两侧上部坡面波压强时程变化Fig.11 The time-history curves of the wave pressure at the measuring points along the two sides(left and right) of the whole slope filling-type sea road 由于波浪条件与作用时间完全一样,大块石护坡型式和小块石护坡型式的进海路受波浪冲击力变化情况与整体式进海路几乎大致相同,这里不再赘述。 本文应用ADINA软件的流固耦合功能,进行波浪作用下3种不同护面型式的填筑式进海路的数值模拟计算。本文应用ADINA软件对填筑式进海路进行数值模拟,流体采用有限体积法,固体结构采用有限单元法,并实现流固耦合,对波浪作用下整体斜坡式、大块石护面、小块石护面三种不同结构型式的填筑式进海路进行了数值模拟计算。根据计算结果,定性分析了各种结构型式进海路的位移、应力应变以及所受的波压强情况,得出结论如下: 1)整体斜坡式进海路由于作为一个整体受力,位移最小;小块石护面进海路的护面块石作为松散结构,位移最大;进海路静水面附近上下约半个波高处及坡脚处受波浪作用影响最大,建议在此处通过增大护面块石的重量或铺设护底块石以防止结构失稳破坏。 2)验证了加设肩台的复式坡面相对单一坡面消浪效果较好,受波浪冲击力较小,但在肩台折角处容易出现应力集中,可以通过铺设护面块体进行防护。工程设计时建议根据地形合理选用复式坡面型式。 由于本文在进行进海路受力分析时边界条件进行简化,不考虑海底地基的作用,只研究了进海路与波浪之间的相互作用,对于海底地基—进海路—波浪三者相互作用的情况仍有待进一步探究。同时,对于复式断面最有利的肩台位置也有待进一步研究。 参考文献: [1] 李巨川.滩海油田进海路断面结构优化及防护措施研究[J].石油工程建设,2008,34(3): 12-17. [2] 林金兰,朱晓飞,王褆卿.极浅海进海路的设计探讨[J].石油工程建设,2005,31(4):24-26. [3] 赵海培,闫相祯.浅滩海地区海工构筑物型式及发展趋势[J].石油工程建设,2009,35(51):92-96. [4] 刘莎莎,顾煜炯,惠万馨,等.基于边界造波法的波浪数值模拟[J].可再生能源, 2013,31(2):100-103. [5] 刘加海,杨永全,张洪雨,等.二维数值波浪水槽波浪生成过程及波浪形态分析[J].四川大学学报:工程科学版,2004,36(6):28-31. [6] LU Y J, LIU H, WU W, et al. Numerical simulation of two-dimensional overtopping against seawalls armored with artificial units in regular waves [J]. Journal of Hydrodynamics:Ser. B, 2007,19(3): 322-329. [7] ZHANG H, ZHANG X L, JI S H. Recent development of fluid-structure Interaction capabilities in the ADINA system[J]. Computers and Structures,2003,81(8-11):1071-1085. [8] BATHE K J, ZHANG H. Finite element developments for general fluid flows with structural interactions[J]. International Journal for Numerical Metheds in Engineering,2004,60(1):213-232.1.2 模型边界条件

1.3 进海路结构型式
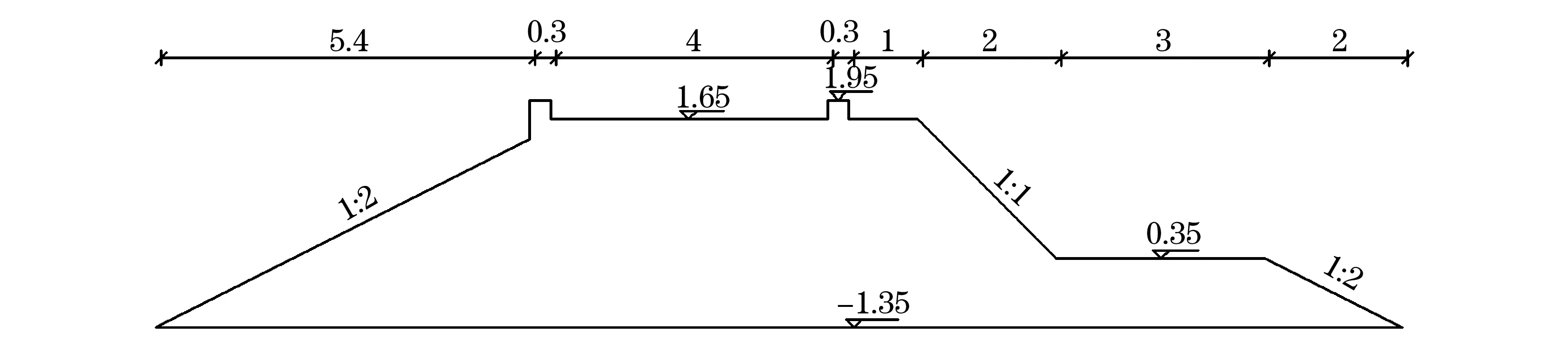

2 流固耦合边界处理
3 数值计算结果分析
3.1 数值计算工况条件


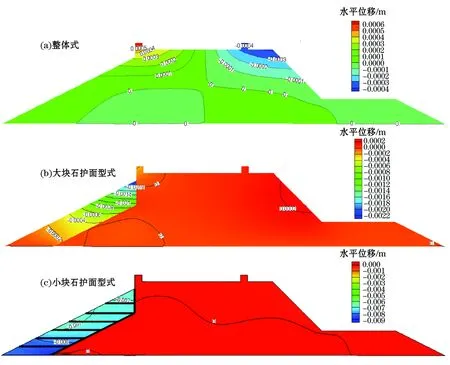
3.2 波浪作用下进海路位移结果分析
3.3 波浪作用下进海路应力应变结果分析
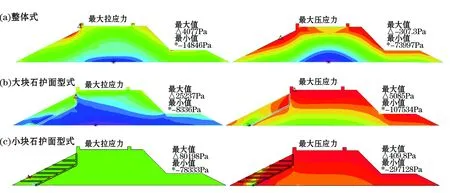
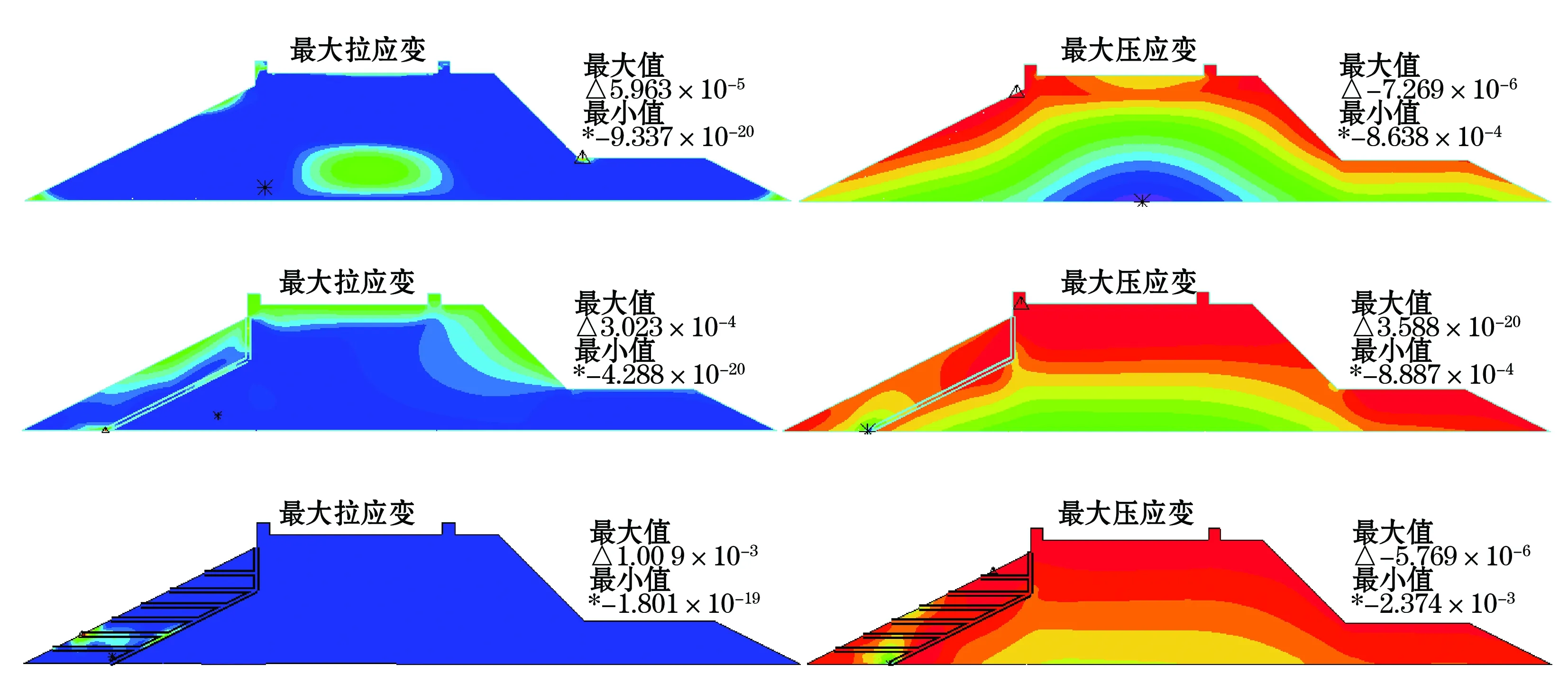
3.4 波浪作用下进海路波压强结果分析


4 结 论
