钢筋混凝土板式楼梯的非线性有限元分析

李艳娇，李瑞敏

（1.沈阳建筑大学 建筑设计研究院，辽宁 沈阳 110015；2.沈阳机床（集团）有限责任公司 设计研究院，辽宁 沈阳 110142）

混凝土板式楼梯因其设计和施工简单、外形美观等优点，成为建筑工程中应用非常广泛的一种楼梯形式.在实际工程的设计中，为了简化计算，通常把梯板、梯梁和平台板都简化为仅受竖向载荷的受弯构件.实际上，在水平地震作用下，梯板为拉弯和压弯构件，梯柱为双向受剪和受弯构件，平台梁和平台板在梯板的斜撑作用下为空间弯、剪、扭矩复杂受力构件［1］，所以实际受力状态与理论计算之间必然存在着一定的误差.随着计算机技术在工程应用领域的不断发展，人们可以通过有限元分析的方法对结构进行更为精确的分析.为了更加准确地了解混凝土板式楼梯的实际受力状况，本文基于大型通用有限元软件ABAQUS对一实际工程中的钢筋混凝土板式楼梯进行了精细化的有限元建模与分析，为结构工程师提供一些参考.

1 工程概况

某二层钢筋混凝土框架结构工程中的楼梯设计为钢筋混凝土板式楼梯，混凝土强度等级为C30，钢筋屈服强度为360MPa.受建筑条件的限制，梯柱宽仅能取200mm，考虑到梯柱在地震中受到较大剪力，为了提高其抗震性能，设计中对梯柱箍筋进行全高加密.在竖向及水平地震作用下，梯板不仅受到弯矩作用，还会受到较大轴力，所以梯板负筋沿板通长布置.休息平台高1.5m，楼层高3 m，结构平面尺寸见图1.平台板钢筋直径8mm、间距200mm，双层双向配筋，其他构件的配筋见图2.

2 有限元模型的建立

2.1 建模方法、单元、材料模型的选择

钢筋混凝土材料是由钢筋与混凝土这两种力学性能差别较大的材料组合而成的复合材料，所以对它的精确模拟是很复杂的.目前主要有整体式、组合式和分离式三种建模方法.整体式建模方法是指将钢筋混凝土看作是一种连续均质的材料，材料的本构是钢筋和混凝土共同作用的体现；组合式建模方法是假设钢筋与混凝土之间粘结良好，将二者分层组合或采取带钢筋的等参单元；分离式建模方法是指将混凝土和钢筋分别建立模型并选择合适的单元，通过连接单元或相互作用考虑二者之间的相互作用关系.本文采取分离式建模方法，混凝土与钢筋的相互作用通过ABAQUS软件的“嵌入”功能使二者自由度耦合，不考虑混凝土与钢筋之间的粘结滑移作用.由于本文主要进行楼梯结构的整体受力及变形分析，不进行构件内部的微观受力机理的研究，所以不考虑钢筋与混凝土之间的粘结滑移作用，这样会使得结构承载力的计算结果偏高，但对于结构整体的受力特点影响不大.

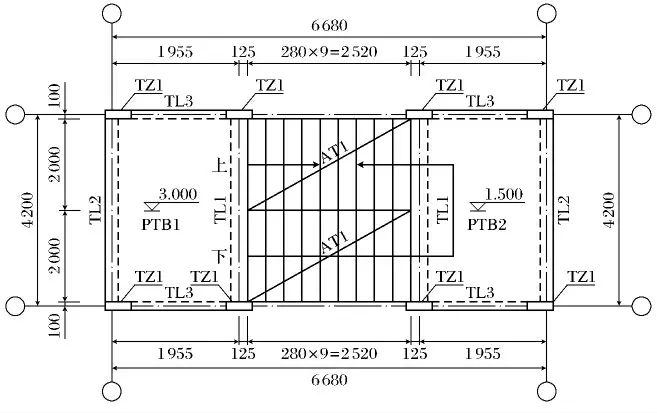
图1 楼梯平面图（mm）Fig.1 The ichnography of stair（Unit：mm）

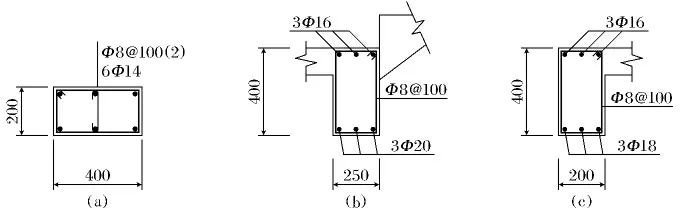
图2 楼梯构件配筋图（mm）Fig.2 The rebar diagram of stair members（Unit：mm）

ABAQUS 单元库中提供了广泛的单元类型，可以适用不同的结构类型和几何特征的需要［2］.C3D8R 单元是三维八节点线性缩减积分单元，它是实体单元的一种，可以模拟几乎任何形状的结构.它的优势在于减少计算时间，在网格划分合理的情况下具有很好的计算精度，所以本文选用C3D8R 单元来模拟混凝土.T3D2单元是二节点三维桁架单元，它仅受轴向的拉力或压力.由于钢筋是一种细长型的材料，通常可以不考虑它的抗剪作用［3］，所以本文用T3D2这种线形单元来模拟钢筋的力学行为.

材料模型的选择是有限元模拟的基础，对模拟的结果有很大的影响.混凝土由于其组成材料的多样性及不均匀性，其力学行为比较复杂，但主要表现为受拉开裂破坏和受压破碎破坏，且抗压强度远大于抗拉强度.混凝土受拉时，主要表现为脆性，具有较小的不可逆变形，因此工程上可以把它视为弹性材料.混凝土受压时，其内部裂纹的开展是导致其破坏的根源，而混凝土的破坏则经历了内部裂纹产生、扩展和延伸直至混凝土断裂成碎块而失去承载力的过程，这个过程是连续的.ABAQUS软件为混凝土提供了混凝土弥散裂缝模型、混凝土开裂模型和混凝土塑性损伤模型，其中的混凝土塑性损伤模型考虑了材料拉压强度的不同，将损伤指标引入模型来描述混凝土材料的刚度退化.单轴拉伸时在应力达到单轴抗拉强度前为弹性，材料达到破坏应力时产生裂缝；单轴压缩时，材料经历应力达屈服应力前的弹性阶段、屈服后的强化阶段和极限应力后的软化阶段，适用于中等围压下的混凝土构件的模拟，可用于往复加载和动态加载，收敛性好［4］，本文选用该模型模拟混凝土.对于混凝土材料的单轴受压和受拉的应力－应变关系，本文采用《钢筋混凝土结构设计规范》GB 50010—2010［5］附录C 中给出的混凝土本构关系曲线，具体见规范.混凝土弹性模量30 GPa，泊松比0.2，密度2 500kg／m3.

钢筋的本构模型主要有三种：理想弹塑性的双直线模型，适合描述流幅较长的钢筋；弹塑性强化的二折线模型，适合描述没有明显流幅的高强度钢筋或钢丝；弹塑性强化的三折线模型，适合描述流幅较短的钢筋［6］.相对于混凝土材料，钢筋的材质均匀，力学计算假定与实际受力状态比较符合，可视为一种理想材料来输入其本构关系.本文钢筋采用理想弹塑性双直线本构关系模型，认为钢筋在达到屈服点之前是弹性的，在屈服点之后是完全塑性的.钢筋弹性模量200GPa，泊松比0.3，密度7 800kg／m3.

2.2 网格的划分及边界条件的设定

网格类型选用计算速度快且精度高的结构化六面体网格，网格划分采取尺寸由大到小的原则，两次划分所得计算结果的差值小于5%时即停止，确定采用最后一次划分的网格尺寸.本文经过试算确定最小网格尺寸为0.05m.混凝土和钢筋的有限元模型分别见图3、图4.

图3 混凝土有限元模型Fig.3 The finite element model of concrete

图4 钢筋有限元模型Fig.4 The finite element model of rebar

边界条件为约束梯柱底面及第一跑楼梯与地面接触部位的所有自由度.

2.3 载荷状况

竖向载荷包括结构自重及2kPa的面层及抹灰载荷，活载荷为3.5kPa［7］；水平地震作用通过对结构施加水平位移载荷近似考虑，根据《建筑抗震设计规范》［8］5.5.5条规定，混凝土框架结构的最大弹性层间位移角不应大于1／550，本文将结构的水平位移加载至10 mm（层间位移角1／300），使材料进入弹塑性来考察结构的受力状况.文献［9］研究表明，顺梯板方向楼梯类似框架结构的支撑，在该方向楼梯与框架间相互作用远大于垂直梯板方向，所以本文在楼层处的顺梯板方向对楼梯施加水平位移载荷.水平位移的施加通过在楼层处梁两端设置弹性钢垫块与梁耦合完成，这样可以避免在一点处施加而产生的应力过度集中问题.

楼梯的常规设计仅考虑竖向载荷作用，不进行抗震设计.所以本文分别对结构在竖向载荷作用下、竖向载荷及水平载荷共同作用下两种状况进行分析.

3 结果分析

3.1 竖向载荷作用下的结果分析

3.1.1 应力分析

图5为竖向载荷作用下混凝土的Mises应力云图，从图中可以看出，混凝土应力较大的部位主要集中在梯板与梯梁的连接处、梯梁和平台板跨中、梯柱的柱顶和柱脚.最大应力为2.0MPa，出现在梯梁跨中的下部.图6为钢筋的Mises应力云图，从图中可以看出，TL1 是梯板与平台板的支座，受力最大，所以TL1跨中下部钢筋应力最大，最大应力为9.545MPa，但远小于钢筋的屈服强度.由上述分析可知，由于本文的楼梯在设计中采取了抗震加强措施，所以在竖向载荷作用下材料的应力远小于其设计强度，结构完全满足日常使用的要求.

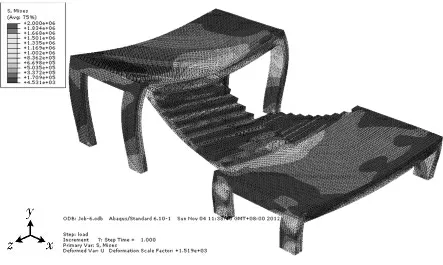
图5 竖向载荷下混凝土Mises应力云图Fig.5 The Mises stress contour of concrete under vertical load

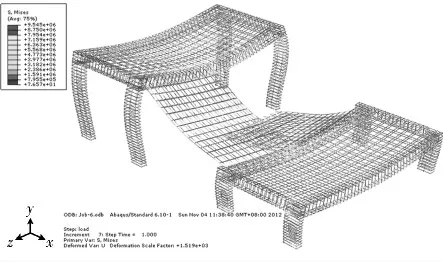
图6 竖向载荷下钢筋Mises应力云图Fig.6 The Mises stress contour of steel under vertical load

3.1.2 变形分析

图7为结构竖向位移云图，从图中可以看出，梯梁跨中和梯板跨中内侧竖向位移最大，最大值为0.46mm.可见，梯板沿宽度方向的位移并不相同，而是内侧位移大于外侧位移.《混凝土结构设计规范》［5］3.4.3规定楼梯受弯构件的挠度限值为l0／200（l0为构件的计算跨度），本文得到最大挠度为0.46mm，仅为计算跨度的1／9130，远小于规范的限值，说明仅在竖向载荷下常规的简化设计方法完全满足规范对结构变形的要求.

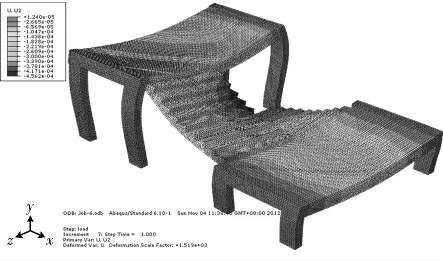
图7 竖向载荷下结构竖向位移云图Fig.7 The vertical displacement contour of structure under vertical load

3.2 竖向和水平载荷共同作用下的结果分析

3.2.1 应力分析

在竖向载荷和水平位移载荷共同作用下，计算结果显示，在水平位移加载至2.5mm 时休息平台处的柱底钢筋应力最先达到屈服，随着位移的增大，屈服区域不断增多.水平位移达到10mm 时，混凝土的Mises应力云图和等效塑性应变云图见图8和图9，钢筋的Mises应力云图见图10.从图中可以看出，应力较大部位集中在休息平台处梯柱的柱底和柱顶及梯梁的跨中，塑性应变集中在平台处梯柱的柱底和柱顶.由上述分析可见，楼梯在常规设计时，虽然采取了加密箍筋及梯板双层双向配筋等加强措施，但楼梯在较小水平位移时梯柱钢筋便进入屈服状态，主要是由于休息平台处的梯柱形成了短柱，受力明显大于楼层处的梯柱.

图8 竖向和水平载荷下混凝土Mises应力云图Fig.8 The Mises stress contour of concrete under vertical and horizontal load

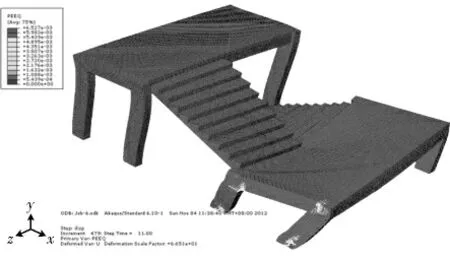
图9 竖向和水平载荷下混凝土等效塑性应变云图Fig.9 The equivalent plastic strain contour of concrete under vertical and horizontal load

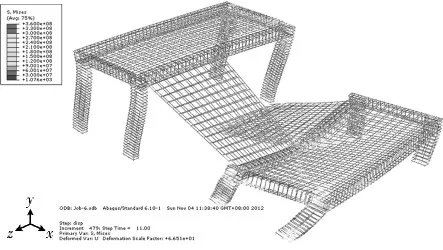
图10 竖向和水平载荷下钢筋Mises应力云图Fig.10 The Mises stress contour of rebar under vertical and horizontal load

3.2.2 变形分析

图11为结构的一个加载点处的水平力－位移曲线，在位移较小时，水平力和位移成线性关系，随着位移的增大，位移的增速大于力的增速，说明材料逐渐进入弹塑性阶段，结构的承载力降低.图12为结构在水平位移为10mm 时的竖向位移云图，最大竖向变形出现在梯板与梯梁和休息平台中部相交的位置，最大竖向位移为7.07mm，满足规范的限值要求.

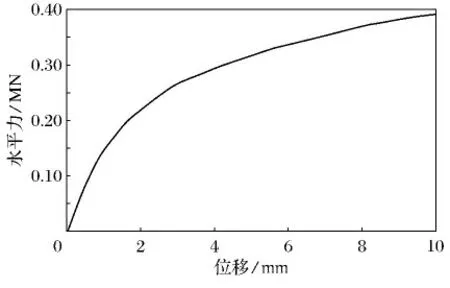
图11 水平力－位移曲线Fig.11 The horizontal force－displacement curve

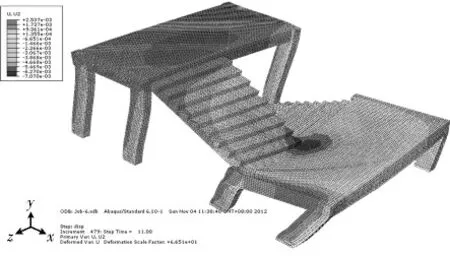
图12 竖向和水平载荷下结构竖向位移云图Fig.12 The vertical displacement contour of structure under vertical and horizontal load

4 结 论

（1）ABAQUS可以用于复杂混凝土结构的精细化有限元分析，得到应力及应变等力学参数，为设计者更好地进行结构设计提供参考.

（2）通过简化计算设计的混凝土板式楼梯在日常使用情况下完全满足结构的承载力和变形要求.

（3）在竖向载荷和水平载荷共同作用下，休息平台处的梯柱形成了短柱，其受力明显大于楼层处的梯柱，钢筋极易进入屈服状态.

（4）采取箍筋加密等加强措施对限制结构竖向变形作用明显，但对减小水平载荷下钢筋的应力作用不大，所以楼梯的水平荷载荷不容忽视，应加强地震作用下楼梯的计算和分析.

［1］沈靓，柳炳康，张瑜中，等.汶川地震中框架楼梯典型震害分析与有限元计算［J］.工程抗震与加固改造，2010，32（4）：114－119.（Shen Liang，Liu Bingkang，Zhang Yuzhong，et al.Typical Seismic Damage Analysis and Finite Element Calculation of Stair in Framein Wenchuan Earthquake［J］.Earthquake Resistant Engineering and Retrofitting，2010，32（4）：114－119.

［2］ABAQUS Analysis User’s Manual［M］.USA：ABAQUS Inc.，2004.

［3］于群，叶文超.无粘结预应力混凝土梁非线性有限元分析［J］.沈阳大学学报：自然科学版，2012，24（3）：75－77，86.（Yu Qun，Ye Wenchao.Nonlinear Finite Element Analysis of Unbonded Prestressed Concrete Beam［J］.Journal of Shenyang University：Natural Science，2012，24（3）：75－77，86.）

［4］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京：机械工业出版社，2006：28－62.（Shi Yiping，Zhou Yurong.ABAQUS Finite Element Example Explanation［M］.Beijing：Machinery Industry Press，2006：28－62.）

［5］中华人民共和国住房和城乡建设部.GB 50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.（Ministry of Housing and Urban－Rural Development.GB 50009—2010Code for Design of Concrete Structures［S］.Beijing：China Architecture ＆Building Press，2010.）

［6］庄茁，张帆，岑松.ABAQUS 非线性有限元分析与实例［M］.北京：科学出版社，2005：239－243.（Zhuang Zhuo，Zhang Fan，Cen Song.ABAQUS Nonlinear Finite Element Analysis and Instance［M］.Beijing：Science Press，2005：239－243.）

［7］中华人民共和国住房和城乡建设部.GB 50009—2012建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012：14－16.（Ministry of Housing and Urban－Rural Development.GB 50009—2012 Load Code for the Design of Building Structures［S］.Beijing：China Architecture ＆ Building Press，2012：14－16.）

［8］中华人民共和国建设部.GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010：46－47.（Ministry of Construction.Code for Seismic Design of Buildings GB 50011—2010［S］.Beijing：China Building Industry Press，2010：46－47.）

［9］吴小宾，冯远，熊耀清，等.带楼梯框架结构静力推覆分析及弹塑性性能研究［J］.建筑结构，2011，41（3）：31－35.（Wu Xiaobin，Feng Yuan，Xiong Yaoqing，et al.Pushover Analysis and Research of Elastic－plastic Performance for Frame Structure with Staircase［J］.Building Structure，2011，41（3）：31－35.）