ANSYS的两自由度宽频压电能量收集装置性能分析

张斯阳， 曾 琴， 孙 科， 陶孟仑， 陈定方

(武汉理工大学智能制造与控制研究所，湖北 武汉430063)

基于振动的MEMS能量收集装置具有非常低的能量密度，可用于无线传感器．微振动功率收集装置的关键问题是设备的谐振频率不匹配的环境振动频带．环境振动的频率从几Hz到几百Hz各不相同，但大多数微观结构的谐振频率均在几kHz左右，而且大部分的微观结构谐振带宽很窄，因此对其拓宽带宽的研究很有必要．

1 国内外宽频压电能量收集装置发展现状

从1969年Wen H Ko提出一种采集心跳活动能量的小型压电悬臂梁式能量采集器[1]以来，世界上许多研究团体开展了一系列关于压电式能量采集器的研究．

韩国Jeong S J 研究小组制作了基于双层压电片的能量采集器：当上下压电层的厚度不同时，在比较近的频率范围内会出现 2个共振频率，这样就增加了器件的频率响应带[2]．弗吉尼亚理工大学的 Erturk A 等人设计了一种 L 型悬臂梁结构[3]，传统的直线型悬臂梁结构的一、二阶固有频率之间至少相差6 倍，通过优化设计的 L 型悬臂梁的前两阶固有频率只相差1 倍，振动能量可以在在一、二阶模态之间传递．

华中科技大学于 2008 年提出了采用悬臂梁阵列结构的方法[4]．2010年南京航空航天大学陈仁文等发明了一种蒲公英状多方向、宽频带压点振动能量收集装置[5]．2011年上海交通大学的马华安等，提出的一种通过磁力的引入使其在低频下工作的、宽频的压电振动能量采集器，与传统无磁铁振动式压电能量采集器相比，有效地拓展了5 Hz的工作频带[6]．2011年上海交通大学刘景全等发明了基于PMNT压电单晶的MEMS宽频振动能量采集器，制备的器件可以在较宽的环境振动范围内输出较大稳定的功率[7]．2012年南京航空航天大学侯志伟等人，提出了一种新颖的多方向振动能量收集装置的设计结构，该装置的换能部分采用了Rainbow 型压电结构，该装置经过优化后，在Y向激励时，其输出的总电能为 37.146 μJ，比优化前提高了30.82%；当沿装置体对角线方向激励时，结构装置输出的总电能为58. 715 μJ，比优化前提高了 29.24%[8]．

2 宽频压电能量收集装置

2009年，中南大学的Z T Yang与美国内布拉斯加大学林肯分校的J S Yang合作，对相连的振动双压电晶片梁结构进行了研究[9]，理论模型如图1所示，发现如果对固有频率相近的双压电晶片梁进行弹性连接与电连接，就可以获得宽频带的电输出．

图 1 相连振动双压电晶片梁结构的理论模型

周围环境中的机械振动能量频率范围很广，压电俘能器作为一个在谐振频率工作的器件，其电能输出由频率决定．当驱动频率达到俘能器结构的特定谐振频率的时候，电能输出最大[10]．

此结构通常情况下有两个谐振峰，谐振峰之间的距离对梁右端悬挂质量块的质量非常敏感，两个质量块质量越接近，其谐振峰的距离越近，这两个离得比较近的谐振峰就构成了一个宽的频率带，在这个频率带内，输出电能非常大，一种特殊情况就是当两个质量块质量相同时，这两个谐振峰合并成一个谐振峰．在两个梁之间设计弹簧，对于拓宽系统谐振频率非常有利，系统能够在较宽频率范围内高效吸收环境中振动的能量．

3 有限元分析

本文将单自由度悬臂梁(图2)、二元阵列悬臂梁结构(图3)、两自由度悬臂梁(图4)利用ANSYS软件进行模态分析和谐响应分析，得出各个压电悬臂梁结构的在不同频率环境下所输出的电压，找到输出电压与频率的关系，证明两自由度悬臂梁可起到拓宽带宽的作用．

以上三种压电悬臂梁长度均为30 mm,宽度均为6 mm，压电层的厚度均为0.12 mm，基层厚度均为0.2 mm(压电陶瓷片与金属片的厚度比度产生的电压有影响，当压电陶瓷片与金属片厚度比为0.6时产生电压最大)．压电材料为PZT-5H,基层材料为铜，质量块材料为镍．质量块的长宽高分别为6 mm、6 mm、4 mm．两自由度压电悬臂梁以弹簧连接．压电层上下表面均设有电极．

图 2 单自由度悬臂梁

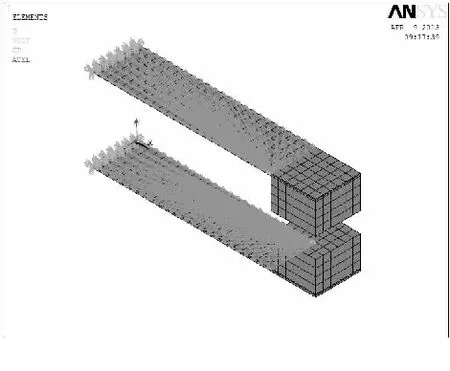
图 3 二元阵列悬臂梁

图 4 两自由度悬臂梁

对这三个模型进行模态分析．模态分析用于确定设计结构或机器部件的振动特性，即结构的固有频率和振型，给出模态参数和系数．三种结构的四阶模态如表1所示．

表1 三种结构的前四阶固有频率 Hz

谐响应分析是分析结构在承受随时间正弦(简谐)变化载荷作用下稳态响应的一种技术．分析可以得到输出电压随频率变化的情况．在一阶固有频率环境下对三种结构进行谐响应分析，结果分别如图5、图6和图7所示．

图 5 单自由度悬臂梁谐响应分析

图 6 二元阵列悬臂梁谐响应分析

图 7 两自由度悬臂梁谐响应分析

在谐响应频率f0下，压电层可产生电压的最大值，在f0两边分别存在f1和f2，且在f1和f2频率条件下振动所产生的电压为最大值的1/√2倍，谐响应带宽定义为

B=|f2-f1|．

从图5可得，此单自由度悬臂梁谐响应频率f0为64.5 Hz，带宽B约为2.7 Hz(63.1～65.8 Hz)．从图6知，二元阵列悬臂梁谐响应频率f0为75.0 Hz，带宽B约为3.8 Hz(73.4～77.2 Hz)．从图7可知，两自由度悬臂梁谐响应频率f0为177.3 Hz，带宽B约为7.7 Hz(174.8～182.5 Hz)．从以上数据可以看出，二自由度悬臂梁不仅可以提高压电能量收集装置的谐振工作频带宽度，且其拓宽频带的效果优于二元阵列悬臂梁．

三种结构的压电悬臂梁在一阶和二阶模态一个周期内的振型不尽相同，图8截面为梯形的两自由度压电悬臂梁．

图 8 二自由度梯形压电悬臂梁

图8为四种结构压电悬臂梁在一阶振型图，图9为四种结构压电悬臂梁在二阶振型图．

(a)单自由度悬臂梁一阶振型图

(b)二元阵列悬臂梁一阶振型图

(c)两自由度矩形悬臂梁一阶振型图

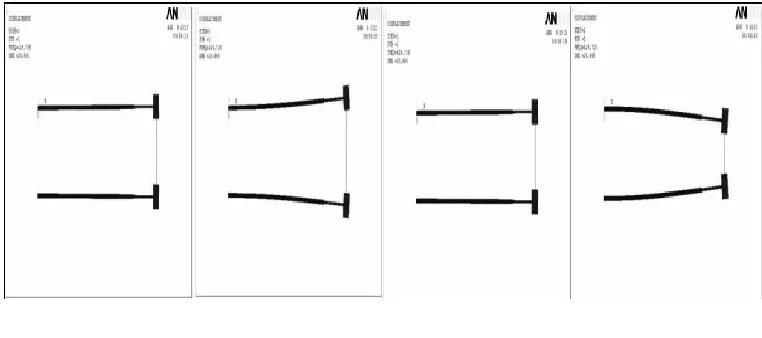
(d)二自由度梯形悬臂梁一阶振型图图 9 四种结构压电悬臂梁一阶振型图

从图9可以知，前三种结构在一个周期内的一阶振型基本相同，主要位移在竖直方向上，但图8c中结构的振幅明显大于前两种结构，且其已发生比较明显的弯曲形变．图8d中结构的振型情况明显与其他三个结构不同，其两个振子的运动方向始终保持相反．

(a)单自由度悬臂梁二阶振型图

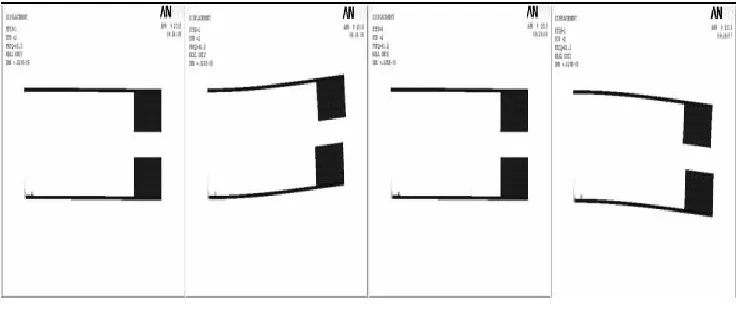
(b)二元阵列悬臂梁二阶振型图

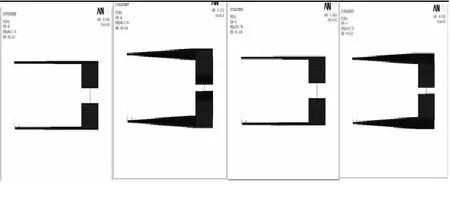
(c)两自由度矩形悬臂梁二阶振型图

(d)二自由度梯形悬臂梁二阶振型图图 10 四种结构压电悬臂梁二阶振型图

与图9相比，图10二阶振幅明显要大于一阶振幅．图9a、b、d的运动方向基本一致，而图9b中的结构梁的主要变形不再是竖直方向，而是水平方向上的翻转变形．图9d与图10d相对比，两个振子的运动方向由一阶中的异向变为了二阶中的同向．

4 结束语

本文分别对参数相同的单自由度压电悬臂梁、二元阵列压电悬臂梁和两自由度压电悬臂梁进行建模．通过模态分析，得到了这三种结构的前四阶固有频率；通过谐响应分析，得到各个结构的输出电压随频率的变化曲线，获得了三种结构的谐响应带宽分别为2.7 Hz， 3.8 Hz和7.7 Hz．可以发现两自由度悬臂梁的谐响应带宽远大于单自由度的谐响应带宽以及大于二元阵列悬臂梁的带宽，可见两自由度悬臂梁可以拓宽频带．本文并未将两自由度悬臂梁与三自由度以及更多自由度的悬臂梁进行比较，因而并不能完全看出两自由度的优势，这也是笔者在后期的研究中需要改进的地方．

[参考文献]

[1] Wen H Ko. Piezoelectric energy converter for electronic implants[P]. US Patent 3,456,134, Patent and Trademark Office, 1969.

[2] Jeong S J，Kim M S，Song J S． Two-layered piezoelectric benderdevice for micro-power generator[J]． Sensors and Actuators，2008，148( 1) : 158 - 167．

[3] A. Erturk J M. Renno D J. Inman. Piezoelectric Energy Harvesting from a L-Shaped beam-mass structure with an application to UAVs[J]. Journal of intelligent material systems and structures, 2009,20(5), 529-544.

[4] Xue H, Hu Y T, WANG Q M.Broadband piezoelectric energy harvesting devices using multiple bimorphs with different operating frequencies[J]. IEEE Transactions on ultrasonics ferroelectrics and frequency control, 2008, 55:2 104-2 108.

[5] 陈仁文,刘祥建,焦丽娟，等．多方向、宽频带压电振动能量收集装置[P]. 中国: CN 102013837A,2011.04.13.

[6] 马华安, 刘景全, 唐 刚，等. 一种宽频的磁式压电振动能量采集器[J]. 传感器与位系统, 2011, 30(4): 66-68.

[7] 刘景全,唐 刚,杨 斌，等. 基于PMNT压电单晶的MEMS宽频振动能量采集装置[P]. 中国: CN 102544349 A,2012.07.04.

[8] 侯志伟, 陈仁文, 刘祥建. 多方向压电振动能量收集装置及其优化设计[J]. 振动与冲击, 2012, 31(16): 33-37.

[9] Yang Zengtao, Yang Jiashi. Connected vibrating piezoelectric bimorph beams as a wide-band piezoelectric power harvester[J]. Journal of Intelligent Material Systems and Structures, 2009, Vol.20:569-574.

[10] 杨增涛.新型压电器件的力电祸合分析与结构设计[ D].湖南：中南大学图书馆,2009.