基于启发式分支定界的单间作业车间优化算法

银 莉, 王 彬, 汪俊亮, 陈定方

(1 武汉理工大学智能制造与控制研究所， 湖北 武汉 430063； 2 浙江海洋学院船舶海洋工程系， 浙江 舟山 316000)

在离散制造系统中，调度问题种类繁多，其中单件车间调度问题(job-shop scheduling problem，JSP)是最基本、著名的调度问题，也说是NP难问题，不可能找到精确求得最优解的多项式时间算法．求解(n/m/J/CMAX)问题，利用分支定界算法、人工智能方法、神经网络方法、遗传算法等方法均有不同程度的调度效果[1]．本文根据JSP问题的调度特征，在考虑加工平衡和压缩空闲时间的基础上，并采用C#语言编写程序，进行实验验证．

1 单间作业车间优化调度的数学描述

借助线性不等式来表示调度约束关系，对job-shop调度问题定义如下[2]：

令N={0,1,2,3,…,n,n+1}表示工序的集合，其中n是工序总数，0和n+1分别表示起始和终止工序；M={0,1,2,3,…,m}表示机器的集合；A表示同一工件的前后关系约束的工序对集合，Ek表示机器K上加工的工序对集合．同时，根据加工实情，假设对于第i个作业在第j台机器上的加工时间pij是一定的，其起始时间tij是优化过程中有待确定的变量．且t0=0，p0=pn+1=0．

可以将job-shop调度问题描述如下．目标函数

MinF，

F表示完成作业的总时间，优化的目的是加工总时间最短．

设定约束条件如下．

1)tik≥tij+pij(i=1,2,…，n)，

其中：tij表示第i个工件在第j台机器上的开始加工时间；pij表示加工时间．该约束条件表示每个工件在机器上的加工次序．

2)引入变量

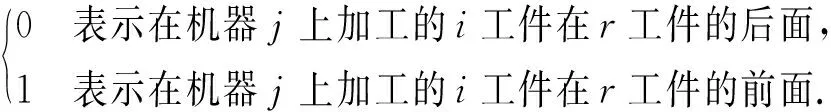
该约束保证每一个工序具有相对独立的加工环境，在其结束加工之前，下一个加工工序不得提前插入．

3)F≥tij+pij(j=1,2…,n,j=1,2…,m).

该约束表示作业完成总时间必须大于或等于最后一件作业的开始时间与加工时间之和．

额外约束如下：1)所有零件都在0时刻到达；2)每个零件在加工流程中经过每台机器，且只经过一次[3]．

2 搜索模型建立

在本问题中单件车间的加工问题归根到底是一个排序问题，根据机器的工序建立分支树模型(图1)[4-5]．分支树的子节点代表当前机器j的加工零件序列{i}，i∈(1,2…n)；第0层代表了起始工序表示所有工件都已按时到达；第j层代表了第j台机器的所有工序排列方案．

图 1 基于机器工序的分支树模型

首先按照启发函数的导向原则，根据计算结果分析出向下搜索最优的路径，得出较优解．若无法得到可行的较优解，则回溯一层，对剩余的一层进行搜索和求解．

通过对算法的分析不难得知，若搜索全局到最优解，算法的时间复杂度为n!m，而若按照启发函数引导搜索得到最优解，则其时间复杂度为n!×m．可见，若能较早得到较优的解，可以较快得到求解结果．

3 启发函数确定

分支过程中的两个重要因素：如何划分问题(分支)和按何种策略选择子问题进行扩展．而在本问题中设置合理的启发函数对短发搜索方向进行引导，可以有效提高搜索效率(整数线性规划的改进)[6]．

在确定启发函数的过程中需要分析(n/m/J/CMAX)问题的作业流程．根据工程实践，工件的加工顺序往往是确定的，而每个工件的工艺路线也具有独特性．

k为该工件目前已完成的工序．加工总时间

其加工进度定义为

(i=1,2,…，n,j、k=1,2,…，m)．

调度算法的目标函数MinF的本质，就是压缩工序的等待时间，即选择该工序之前加工时间最短和的工序进行加工．

综上所述，选用下式作为启发函数：

(i=1,2,…，n,j、k=1,2,…，m)．

4 算法设计

步骤二：判断剩余集是否为空．若为空，判断层次j是否等于m，若是取当前最优解为最优调度方案；若小于m，则将当前层次的调度方案存入Ej．若不为空，则取下一组方案进入步骤三．

步骤四：计算最优解决方案的完工时间F，并输出表示机器的加工工序对集合E．

5 调度实例

采用 Benchmark调度问题对算法进行验证．

表1 8×4Benchmark调度问题

采用本算法对上述问题在C#环境下进行编程求解，执行计算的硬件环境为Core(TM)I7-2630处理器、2GB内存，操作系统为Windows 7．算法的求解结果见图2． 通过对比计算结果，可知本算法的最大完工时间为35，文献[7]的结果(Makespan=39)相比具有优势．

图 2 Benchmark调度问题求解甘特图

上述研究结果证明了算法的可行性、高效性和实用性．本启发式算法依靠启发函数指引算法在层次结构中的搜索方向，采用深度优先的搜索策略，减少了搜索量．测试证明，本算法在提高速度的同时依然具有较高的求解精度，能较快收敛得到最优解．

6 结束语

然而，在实际的生产这种环境极为复杂，需要考虑的因素较多：如工序相关性、机器之间加工的通用性．虽然以上一些约束的增加使得算法在调度过程中体现出了生产系统的专用性，但是为了进一步完善不同加工情况下的算法，在今后的工作中可考虑以上约束和假设．

[参考文献]

[1] 熊禾根，李建军，孔建益,等. 考虑工序相关性的动态Job-shop调度问题启发式算法[J].机械工程学报，2006,42(8):50-55.

[2] 范路桥,常会友,朱旭东. 一种改进的作业车间调度算法及其实现[J].计算机集成制造系统,2005,11(5):673-677.

[3] Edward C. Sewell ,Jason J. Sauppe ,David R. Morrison ,Etc.A BB&R algorithm for minimizing total tardiness on a single machine with sequence dependent setup times[J].J Glob Optim,2012,54:791-812.

[4] Jose M. Framinan. An adaptive branch and bound approach for transforming job shops into flow shops[J].Computers & Industrial Engineering,2007,52:1-10.

[5] 王锡禄，姚伟力，冯恩民. Job-shop调度问题的优化模型及算法[J].系统工程理论与实践，2000(11):84-89.

[6] Christian Artigues, Michel Gendreau, Louis-Martin Rousseau,etc. Solving an integrated employee timetabling and job-shop scheduling problem viahybrid branch-and-bound[J], Computers & Operations Research,2009,36:2 330-2 340.

[7] 张晓东，严洪森. 一类job-shop车间生产计划和调度的集成优化[J],控制与决策，2003,18(5)：581-584.