带质量块单晶压电悬臂梁的建模与仿真分析

曾 琴， 张斯阳， 陈定方， 孙 科， 陶孟仑

(武汉理工大学智能制造与控制研究所， 湖北 武汉 430063)

随着集成电路(IC)制造技术的发展,低能耗集成电路和MEMS技术越来越多地被用到电子设备中来实现节能．压电能量采集器由于其易集成，可适用于任何场合，且能量输出密度大、结构相对简单、易于加工制作等各种优点而受到广泛关注，目前压电能量采集器主要应用于回收人体活动能量和回收外界流体能．然而，耦合因素、频率匹配和应变分布等成为制约该技术应用发展的关键因素[1]．本文通过理论建模与仿真分析，着重研究了带有质量块的单晶片压电悬臂梁的电压输出，并探讨了悬臂梁结构、基层厚度对其发电能力的影响规律，最后在此基础上提出了优化模型，并进行了仿真分析．

1 能量采集器结构和数学模型

1.1 能量采集器结构

压电式振动能量采集器主要利用压电效应，当压电材料应力形变，材料内部正负电荷中心发生偏移，从而产生电动势．常用的压电悬臂梁能量采集器主要由固定支座、支撑层、压电层、质量块组成(图1)．

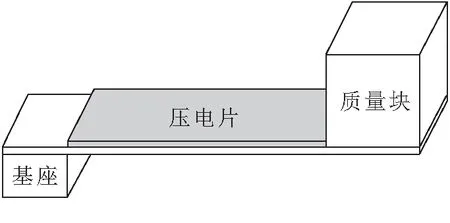
图 1 悬臂梁结构

本文主要采用该模型对其进行耦合分析．压电悬臂梁压电层的长、高分别定义为L1、H1，支撑层的长、高分别为L2、H2，宽均为W．

1.2 数学模型

梁末端质量块的重力作用会使悬臂梁产生弯曲变形(图2).

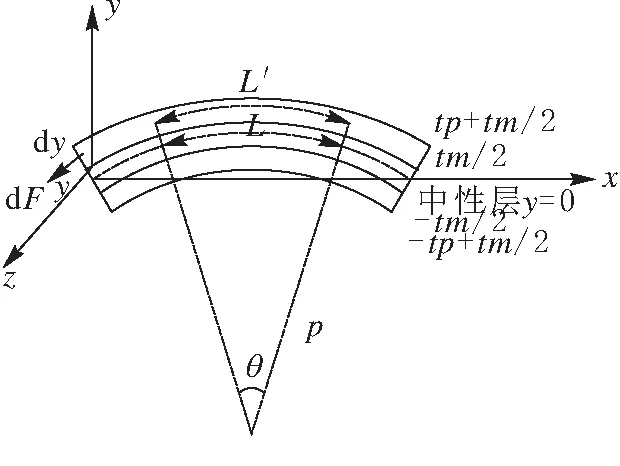
图 2 受力变形

压电方程为[2]

式中：σ为应力，α为应变，ε为介电常数，E为电场强度，D为电位移，c为弹性模量，dxx为压电常数．根据压电方程可知，能量采集器的电压输出与压电片上的应变成正比关系．压电片上总的应力越大，电压输出越大．在悬臂梁上最大应力一定时，应使梁上的应力变化尽可能小，实现应力均匀化，增大压电片上的输出密度，增大电压输出．

2 有限元仿真

在ANSYS中，Solid5,Solid98和Plane13可以用来进行压电材料的仿真，在这里采用Solid5单元作为压电材料进行建模[3]．该单元为六面体单元．支撑层和质量块采用Solid45单元，忽略粘结层的影响，假设支撑层与压电层的位移是一致的．

2.1 模态分析和谐响应分析

选取材料：支撑层为铜，压电层为PZT-5H，质量块为镍，并定义L1=50 mm、H1=0.2 mm、L2=42 mm、H2=120 mm，质量块尺寸为8 mm×8 mm×5 mm，建立ANSYS模型，网格划分，加载，求解后得到三阶模态分析结果：谐振频率f1=23.211 Hz、f2=206.951 Hz、f3=289.659 Hz.，然后进行谐响应分析，频率范围设为0～500 Hz，子步数为50，阻尼为0.02，得到如图3所示的谐响应分析图．

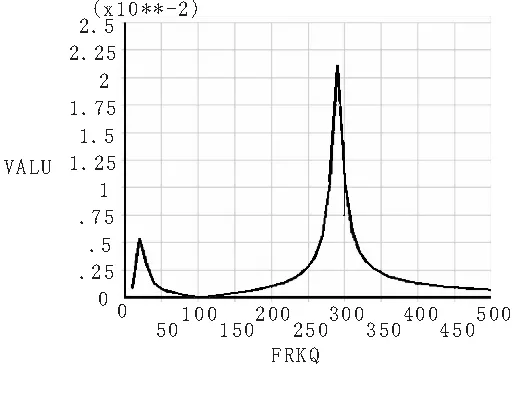
图 3 谐响应图

由图3可见，在固有频率附近，电压输出最大，这为以后设计能量采集装置提供了依据，即使压电振子的固有频率与工作环境接近．考虑到该能量采集装置一般工作在低频范围(200 Hz以下)，本文只考虑一阶固有频率时的电压输出，此时最大电压输出为5.8 MV．

2.2 比较分析

改变支撑层悬臂梁的厚度，分别求得支撑层厚度分别为0.16 mm、0.2 mm、0.25 mm、0.30 mm、0.34 mm时的悬臂梁上的总的应力输出和电压输出，得到总的应力变化(图4)和电压变化图(图5)．

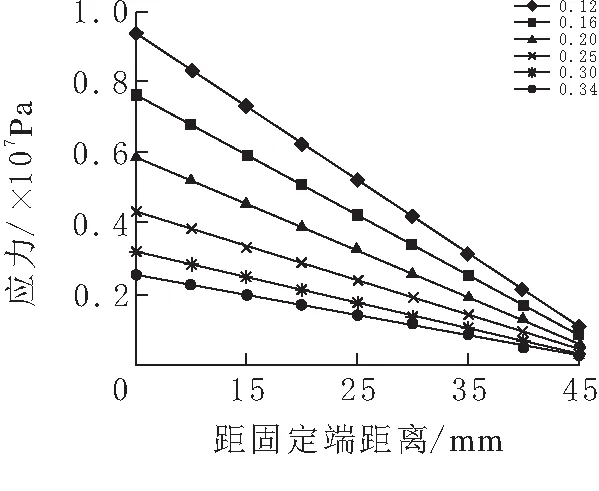
图 4 总的应力随支撑层厚度变化

由图4可见，随着支撑层厚度增加，梁上总应力逐渐减少，与理论是相符的．

图 5 电压随支撑层厚度变化

由图5可见，随着支撑层的厚度增加，电压输出呈现先增大后减小的趋势，在支撑层厚度为0.2 mm时输出电压最大．说明压电悬臂梁支撑层的厚度对电压输出有显著影响．

综合两图发现，增加支撑层的厚度，悬臂梁上的总的应力逐渐减少，但是电压先增大后减小，从理论上来说，电压应该是逐渐减小的．为此重新获取了悬臂梁上沿长度方向的应力，得到如图6所示的沿长度方向应力变化图．

图 6 沿长度方向应力变化图

由图6可见，悬臂梁上的应力曲线出现了交叉，并且有正有负，沿长度方向求取应力和值，得到0.2 mm时和值最大，也是输出电压最大点．说明悬臂梁上的电压输出只与长度方向的应力有关，并且与应力和值成正比关系．

为进一步验证结论，将支撑层设为梯形结构，改变自由端的尺寸，固定端尺寸不变，得到电压输出变化(图7)．

图 7 电压随梁的形状变化图

随着悬臂梁自由端与固定端尺寸比例的增加，电压输出是逐渐增大的，该图从侧面说明了支撑层厚度变化对电压输出的显著影响．随着比例的增加，悬臂梁上沿长度方向应力变化与图6相似，证明上述结论是合理的．

3 结构优化

基于上述研究，提出新的优化模型．该模型选取了最优化厚度，将支撑层厚度定义为0.2 mm，质量块体积不变，改变其形状，其他尺寸均不变，建立如图8所示模型，然后对其进行应力、模态、谐响应分析．

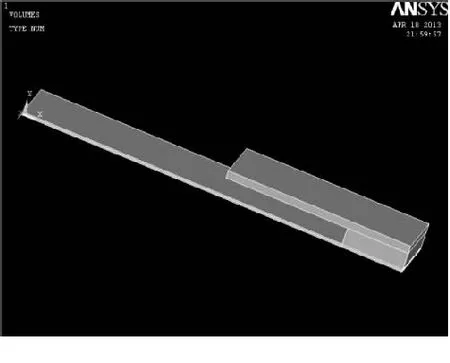
图 8 优化模型

根据求得的一阶谐振频率设置频率范围，进行谐响应分析，得到如图(9)所示谐响应图．

图 9 优化模型谐响应图

从结果上来看，优化模型电压输出为36.7 MV，而在质量块形状不做改变时电压输出为27.6 MV．电压输出明显增大，证明优化模型是可行的．

4 结束语

本文建立了带质量块的单晶压电悬臂梁模型，并用ANSYS软件进行了应力分析、模态分析和谐响应分析，求解出固有频率下电压输出最大；通过改变支撑层结构参数，获取电压变化图，证明支撑层的厚度对电压输出有显著影响，而且呈非线性关系；选取合适的支撑层厚度，有利于提高电压输出，并且对结果进行了解释分析，但是在仿真分析中没有给出最佳的厚度比例．最后根据分析结果提出了优化模型，通过仿真分析，证明优化方案是可行的．从分析结果上看，用ANSYS对压电悬臂梁进行仿真分析，可以降低实验成本，缩短生产周期．

[参考文献]

[1] Roundy S. On the effectiveness of vibration-based energy harvesting [J].Journal of Intelligent Material Systems and Structures, 2005(16): 809-823．

[2] 普里亚 S，茵曼 S. 能量收集技术[M].黄见秋,译.南京：东南大学出版社，2011.

[3] 党莎莎，许 萍. ANSYS13.0多物理耦合场有限元分析从入门到精通[M].北京： 机械工业出版社，2012.