基于DS/AHP的决策方法改进

贺 彦， 熊才权

(湖北工业大学计算机学院， 湖北 武汉 430068)

由于客观事物的复杂性、不确定性以及人类思维的模糊性，对不确定信息下多属性决策(Multi-attribute decision making, MADM)问题研究已引起了人们的极大关注．多属性决策问题通常需要决策者在若干不同的属性上对决策方案表达偏好信息, 常用的分析方法有多属性效用理论[1](Multi-attribute utility theory)和层次分析法[2](Analytic Hierarchy Process, AHP)等．而对于不确定性问题的处理, 证据理论(Dempster-Shafter Theory)能够通过信任函数和似然函数很好地进行解决，显示出了很好的应用前景．Beynon等[3,4]将证据理论与层次分析法相结合，提出了一种DS/AHP的多属性决策方法，给解决不确定多属性决策问题提供了一种新的思路．但是其对基本概率分配函数(BPA)进行计算和合成时比较复杂，为此本文在Beynon等人提出的DS/AHP方法之上提出了一种新的基本概率分配函数的计算和合成方法，此方法能降低原有方法的时间复杂度，其最终合成结果也具有直观性，最后给出一个算例来证明此方法是有效的．

1 基本证据理论

证据理论(又称D-S证据理论)由Dempster于1967年提出[5]，并由他的学生Shafer对其进行推广和完善[6]．该理论除了可以表达由随机性引起的不确定性外，还可以描述由不确切知道和信息不完全所导致的不确定性．下面给出几个证据理论的主要定义.

基本概率分配(basic probability assignment)函数，即Mass函数，该函数映射幂集合中的每一个元素成为区间[0,1]的一个实数．函数的形式化描述为：M：2[0,1]，一般满足下列关系：

1)空集合的Mass通常被定义为0(zero)，M()=0．

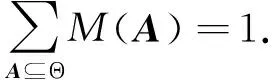
其中对于任何一个集合A∈2，如果M(A)≠0，则A称为焦元(focal element)．

信任函数Bel(A)表示对命题A为真的信任程度，且

似真函数Pl(A)表示A为非假的信任程度，且

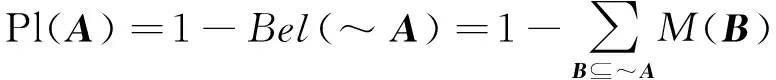
信任函数Bel(A)和似真函数Pl(A)也可称为上下界函数，由它们组成的区间[Bel(A)，Pl(A)]叫做证据区间EI(Evidence Interval)．

在实际的问题中，往往可能同样的证据得到了不同的概率分配函数，我们希望组合所有概率分配函数以产生一个更好的信任评价．假设M1和M2是同一证据的两个概率分配函数，其证据组合为M=M1⨁M2，则有

M() = 0

当合成证据的概率分配函数为多个时，例如：M1,M2, …,Mn，同理，可以根据合成规则M=M1⨁M2⨁…⨁Mn合成如下：

M()=0，

其中

2 DS/AHP方法

DS/AHP方法是Beynon等人利用证据理论组合规则,将AHP方法改造成适应于解决不确定信息问题的方法,以减少计算量,其方法同AHP方法有相似之处．Beynon针对不同属性下有限方案的部分偏好信息集结问题，将证据理论和层次分析法相结合，提出了DS/AHP方法，很好的解决了AHP方法中的问题．Beynon的方法计算过程如下：

步骤1 针对需要解决的问题，把它细分为目标、属性和方案，不过这里与AHP方法不同的是，最底层的方案层不是单个元素，而是决策者对某个属性的方案和方案集的列举．

步骤2 求出各层次上的权重系数，一般从高层到低层．假设某个属性S的权重为P，相关的下一层的方案为F1,F2, … ,Fn，针对这个属性S，每一个方案与识别框架Θ上的方案进行比较，比较的结果构成了一个判断矩阵，判断矩阵的取值用0-6标度值表示．这样可以求出判断A的最大特征值λmax，λmax的标准化特征向量为w=[w1,w2,…,wn]T，即为各个方案相对应的属性S的重要性排序．

其中ɑin是第i个方案与识别框架Θ的方案比较值．1表示与自己本身比较的结果；0表示无法区分焦元之间的相对重要程度．

步骤3 把S属性的权重影响加入矩阵中得到新的判断矩阵A’．具体的方法就是与各个权重值相乘．对修改后的判断矩阵A’求出最大的特征值λmax的特征向量，w=[w1,w2,…,wn]T，这里的特征向量w即是各个方案的基本概率分配函数BPA．

步骤4 将上一步求出的各个基本概率分配函数用经典的证据理论合成法则合成，会得到一个总的BPA函数m，再求出各个方案的不确定性区间[Bel(X),Pl(X)]，则决策者可选取信任函数值最高和似然函数值最高的方案作为备选，再根据给出的决策规则，选出最佳方案．

3 DS/AHP方法的改进

3.1 BPA计算的改进

对于已经构造出的判断矩阵，由于它的对角线、最后一行和最后一列才具有方案与识别框架的比较数值，那么对于这个特殊的矩阵，可以根据矩阵初等变换的性质，直接得到一个一般结果的公式，而不用一步步计算，推导出的结果公式是：

对于一个有n-1个方案正实数的矩阵A，其与识别框架Θ构成一个n阶判断矩阵An+1，那么可以根据矩阵的初等变换有：

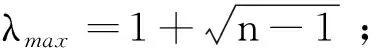
当属性的权重值已知时，那么这个属性的基本概率分配函数值

3.2 BPA合成的改进

本文提出一种按权重比例转化的方法，对BPA的合成方法进行了修改，使之能和DS/AHP方法一样进行决策，还能大大减少计算量．此方法的步骤是：在求出BPA之前的步骤和DS/AHP相同，求出各个属性的每个方案的BPA之后，按权重比例对每个方案的BPA进行转化，转化方法就是每个方案中的元素占识别框架Θ的元素的比例再乘以每个方案中包含这个元素的BPA，结果即是这个焦元的BPA．具体的形式化表述为：

设有一个识别框架Θ={A1,A2,…,An}，对于某个属性下的方案集，其BPA分别为m1,m2, …,mi,mΘ，第k个元素Ak(1≤k≤n)的BPA转化公式为

mP({Ak})=a1m1+a2m2+…

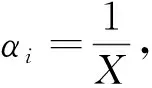
当有n个属性和m个方案的时候，Dempster合成要对每两两属性下的方案的BPA进行合成，合成的时间复杂度为O(mn)，而本文改进的方法不论方案集Θ有多大，只用对每个方案所占权重比例进行分配，时间复杂度始终是O(n)．可以看出这种转化合成BPA方法比用Dempster合成方法在计算量上要少了很多．具体的时间复杂度比较见图1.

图 1 时间复杂度比较图

3.3 合成结果的改进

从DS/AHP方法的最后一个步骤可以看出，虽然DS/AHP方法在一定程度上解决了AHP方法的两两方案比较次数过多的问题，但是它的合成结果不能直接给出最优的决策方案，而只是给出了一个初步的筛选．针对这一点，在原有的BPA合成方法之上，提出了一种新的处理方法．

由上节计算出按权重比例进行转化的BPA值，这些值能构成一个m×n阶BPA矩阵，然后与已知的每个属性的权重组成的1×m阶权重矩阵做矩阵乘法运算即可得到最终每个方案的支持度．具体计算过程如下：

4 算例分析

问题描述：设有一个对公司综合评估选取各项综合评估值最高的决策问题，下面有四家公司，要对四个公司的员工薪水、工作时间、公司环境、发展前景四个角度进行衡量．

对给出的问题进行形式化建模，设有识别框架上的所有的方案集，集合为Θ={A,B,C,D},代表了A,B,C,D四家公司，决策的属性集S={S1,S2,S3,S4}分别代表了考虑的角度，其中S1=薪水,S2=工作时间,S3=公司环境,S4=发展前景．然后根据各个公司的员工对心目中各个属性的重要程度给出了属性的判断矩阵(表1，表2).

表1 决策合适程度量化表

表2 属性S的判断矩阵

根据矩阵理论的初等变化可以求得最大特征值λmax=4.102，对应这个特征值的特征向量即为各个属性的权重(表3).

表3 属性的权重值

由公式进行一致性检验，求得CR=0.034<0.1，所以满足属性间的一致性．然后根据各个公司的员工对每个公司各项属性的了解，给出了公司选择问题的决策矩阵，接着构建每个属性中的方案的集合(表4).由层次结构模型(图2)，再加上决策者对应的偏好可以得表5.

表4 公司各属性的描述

*表示不知道

图 2 层次结构模型

表5 不同属性下的表现度

根据不同属性下的表现度可以构造相应的知识矩阵(表6-9)．

表6 薪金的判断矩阵

表7 工作时间的判断矩阵

表8 公司环境的判断矩阵

表9 发展前景的判断矩阵

构造知识矩阵，首先计算各知识矩阵的特征向量，并把不同影响因素的影响因子看作是相互独立的证据源，把不同影响因素下知识矩阵的特征向量求归一化作为决策的基本概率分配，经过本文改进了的BPA的计算方法处理，计算结果见表10.

表10 各知识矩阵的BPA

对各个属性下的方案按权重比例转化，转化结果为：

根据上节的各个BPA值和各个属性权重进行矩阵运算得表11.由此可见4个公司的排序为：D > C > B > A．表示D公司的员工对公司的评价最高．如果按照原有的DS/AHP算法，用Dempster的合成规则进行合成，得表12.

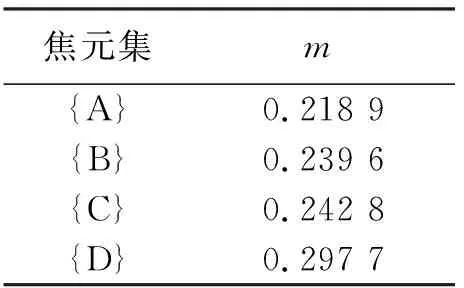
表11 Beynon方法计算得BPA

表12 BPA函数

从表12可以看出，{D}获得了最多的权重指派，其次是{C}，再是{AC}，{B}，{Θ}和{A}．排序表为{D}>{C}> {AC}>{B}>{Θ}>{A}，可见若不加入更多的信息，倾向于D公司的员工对自己的公司评价最高，这与之前使用本文改进的方法得出的结论一致．而本文的方法时间复杂度却降低了．

5 结束语

本文对原有的DS/AHP方法改进只是修改了BPA合成的计算步骤，直接根据决策者给出的偏好信息求出了最后的决策结果，可能从某些方面加大了决策风险．而原有的DS/AHP方法根据备选方案集和对应的偏好信息，一步步对这些方案的影响程度进行更新，最终求出各个方案的影响程度，这样可以有效降低决策风险．决策者应审慎思考这一风险因素,根据实际情况采用不同的方法．

[参考文献]

[1] 徐志新, 奚树人, 曲静原. 核事故应急决策的多属性效用分析法[J]. 清华大学学报(自然科学版),2007(3): 448-451.

[2] Saaty T L. The analytic hierarchy process[M]. New York: McGraw-Hill, 1980.

[3] Beynon M J, Bruce Curry, Peter Morgan. The Dempster-Shafer theory of evidence: An alternative approach tomulti-criteria decision modeling[J]. Omega, 2000, 28(1): 37-50.

[4] Beynon M J. DS/AHP method: A mathematical analysis, including an understanding of uncertainty[J]. European J of Operational Research, 2002, 140(1): 148-164.

[5] Dempster A P. A generalization of bayesian inference (with discussion)[J]. Journal of the Royal Statistical Society Series B, 1968, 30 (2): 205-247.

[6] Shafer G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.