客运专线车站股道分配方案的均衡性研究

刘 淇，王 军，张星臣，陈军华，杜 鹏

（北京交通大学 交通运输学院 1.硕士研究生 2.博士研究生 3.教授 4.讲师 北京 100044）

车站是客运专线铁路运输网络中的关键节点。在车站作业中，股道分配是一项很重要的环节，车站设备的合理使用，直接关系到车站的服务水平与资源的有效配置。对于股道分配问题，限于求解规模的巨大，目前多集中在可行解的分析与建模。文献〔1〕建立多目标股道分配模型，运用多目标规划理论，采用分支定界法对模型进行求解；文献〔2〕建立了以行车交叉干扰小、方便旅客出行和到发线使用均衡性为优化目标的整数规划模型；文献〔3〕将影响股道分配的因素分为软约束和硬约束进行建模并求解；文献〔4〕对运用数学规划的方法来求解到发线运用问题，建立一个到发线运用的混合整数规划模型。

然而，股道分配方案均衡性研究并不系统和深入。如文献〔2〕研究了股道分配方案的均衡性问题，但对均衡性的描述简化为全天股道被占用时间的均衡，这并不能充分说明该方案是否均衡。鉴于此，本文在分析影响均衡性分配的基础上，建立了刻画分配均衡性的指标，并建立股道分配的数学模型，达到评价大型客运站股道分配的均衡性目的。

1 影响股道分配均衡性的因素

客运专线股道分配均衡性是指在列车运行图与车站平面图的时空约束下，为列车分配无冲突的进路和站台，使车站各股道被占用的时间和空闲间隔时间达到均衡以及方便旅客上下车。

列车在车站的行车作业包括接车、停留和发车3个部分，在此过程中需要为列车铺排进路和安排停留到发线，以及满足列车进行各种作业的要求等，另外在客运专线车站还要考虑到旅客乘降的舒适度，这些都会对股道的使用产生影响。影响股道分配均衡性的因素包括列车进路的选择、车站间隔时间、列车去向及线路上下行。

1.1 列车进路的选择 大型客运专线车站衔接方向多，一段时间内接发列车可能比较多，一列列车进路的铺排可能会影响到其他列车进路的选择。当选择不适合时，会导致进路交叉，致使其他列车不能按时接到相应的股道，从而影响了车站的作业能力。

1.2 车站间隔时间 为保证车站作业的安全，只有当前行列车的尾部离开并释放相应的轨道电路区段以后，才能为后行列车开始准备接车进路。因此，对于先后占用同一股道的2 列车，前行列车离去到完全释放到发线的时间，与后行列车开始占用到发线的时间之间的间隔，应满足一定的安全间隔时间。

1.3 列车去向及线路上下行 在不考虑其他条件约束的情况下，车站各股道都可以接发任何去向的列车。但是这样就会产生诸多交叉干扰，反而影响了车站的能力。因此，每个股道应有特定接发列车的方向和种类。

2 股道分配均衡性模型

由于不同的时间段，列车到发的数量有区别且车站股道使用的目的也有区别，因而高峰时期，由于列车到发多，车站可能更多地考虑车站各股道使用均衡性；而在低谷时间段，车站可能更多地考虑如何满足旅客上下车的舒适性。为此，需要对高峰期和低谷期2种情况分别建立模型。

2.1 高峰期目标函数 根据影响股道分配均衡性的因素，建立以股道总体使用均衡性和各股道使用空闲时间均衡性为优化目标。

1）目标函数1：各股道被占用时间均衡的目标函数（见式1），表明目标函数值越小，股道使用越均衡。

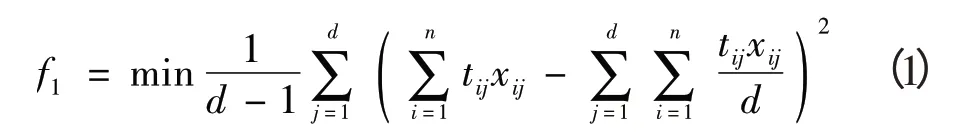
式中：d为车站的股道数；

n为车站一天内到发列车数；

tij为第i 列车接发到到发线j 的总时间，tij=tsi+tLi+tEi；tLi为第i 列车占用到发线时间，由出发时刻和到达时刻得到；

tsi为第i 列车出发作业时间，由车站技术作业标准得到；

tEi为第i 列车到达作业时间，有车站技术作业时间标准得到；

Xij表示第i列车是否使用第j条股道，0，1变量；当Xij=1时第i列车由第j股道接发。

2）目标函数2：股道空闲时间均衡的目标函数（见式2），表明目标函数值越小，股道使用越均衡。

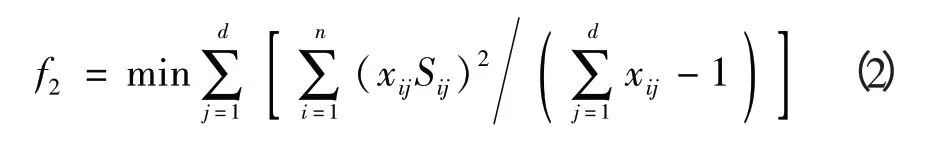
式中：Sij表示第j股道分配给2个相邻列车中间的空闲时间，即，表示同一股道前一列车的离开时间与后一列车到达时间的差。

2.2 低谷期目标函数 低谷期，车站列车比较少，此时要以提高服务质量、方便旅客乘降为核心，为列车安排股道。

目标函数3：方便旅客乘降的目标函数（见式3），表明目标函数值越小，更能方便旅客乘降。

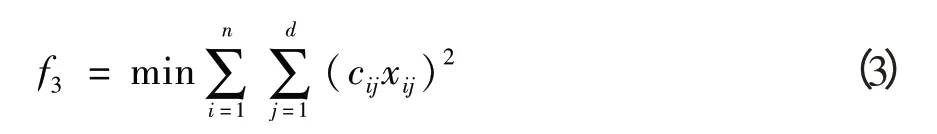
式中：Cij表示列车i使用股道j时方便旅客乘降的权重。

2.3 约束条件

1）列车去向、上下行等引起的约束。根据列车的去向、上下行和个人偏好等情况，将列车i分到对应股道集合Wi中股道进行接发。

2）一列列车至多有1条股道接发，即

3）在一段时间内，1 条股道只能被1 列车占用。记列车i 占用股道j 的时间为，在该段时间内股道j不能在被其他的占用：

式中：tj表示股道j被占用的时间；

ZjW表示j是否被占用，0，1变量；当ZjW=1表示被占用，否则，ZjW=0表示未被占用。

4）进路冲突约束。进路的冲突分为时间冲突和空间冲突。时间冲突是由列车运行图产生的，时间冲突可以通过分配无冲突的空间资源解决；空间冲突需要给予冲突的作业分配无冲突的时间资源。因此，为2列车安排股道时，应避免2种冲突同时出现。

5）同一股道连续接车的时间间隔应满足作业时间要求。假定相继停在股道j的3列车i-1、i、i+1，则他们在车站的时间间隔约束应满足：

Tmin为车站作业最小间隔时间。

3 模型求解

由于建立的模型是多目标非线性规划模型，直接求解存在很大的困难，但可以采用遗传算法进行求解。遗传算法是一种自适应搜索算法，是优秀的全局搜索算法。

3.1 编码形式 采用整数编码方式，染色体长度为需要安排股道的列车数量。每个基因上的数值代表分配给该列车的股道编号。

3.2 初始群体的生成

步骤1：按照列车进站时间顺序初始化列列车，记为集合N=（n1，n2，…，nk）；股道是按照车站的使用方案和空闲开始时间进行初始化，记为D=（d1，d2，…dm，）。

步骤2：产生所有列车可使用股道集合W=（W1，W2，…，Wn），W1表示列车i 可使用股道集合。列车i可使用的股道j需要满足的约束条件包括：股道j应在列车i可使用的股道集合中；列车i的实际到达时间要晚于股道j空闲开始时间，列车i离开时间要早于股道j的结束使用时间，且相邻两列车使用同一股道的时间间隔不小于Tmin。

步骤3：为1 列列车生成1个随机整数bi∈ [1,count（Wi）]，确定列车i 在可使用股道集合中的股道j，更新股道i的开始使用时间；若大于边界时间，则在其他列车可使用的股道集合中将此股道j删去，更新其他列车可使用股道集合；

步骤4：判断Wi+1，Wi+2，Wi+3，…Wn中是否有空集，如果有转步骤2；如果没有，转步骤5。

步骤5：判断i=n 是否成立，如成立转步骤6；如果不成立，则i=i+1转步骤3。

步骤6：所有列车分配完毕，算法结束。

这样循环n 次即可以得到种群数量为n 的一个初始群体。

3.3 适应度函数的选取 适应度函数是算法用于指导搜索方向的惟一准则。由于该问题的目标函数是取得最小值，不能直接作为适应度函数。

1）高峰期的适应度函数

适应度函数1：F1=M-f1

适应度函数2：F2=M-f2

2）低谷期的适应度函数

适应度函数3：F3=M-f3

式中：M为足够大的数。

3.4 遗传算子设计

3.4.1 选择操作 采用比例选择算子，按个体的适应度函数值采用赌轮法来决定个体被选择的概率。

3.4.2 交叉操作 采用随机配对策略将群体中染色体以随机的方式组成配对染色体组，每组以一定的概率进行交叉操作。

3.4.3 变异操作 遗传算法实现变异的方法是赋予每个基因一个相对较小的变异概率。

3.5 终止准则 根据需要，采用确定的迭代次数作为终止规则。

4 案例分析

某客运站是一个双线通过式车站，车站衔接3个方向（A，B，C），共有股道9条，4个站台，其中2条正线、7条到发线，该车站包括2个咽喉，B和C方向在车站的一侧（见图1）。

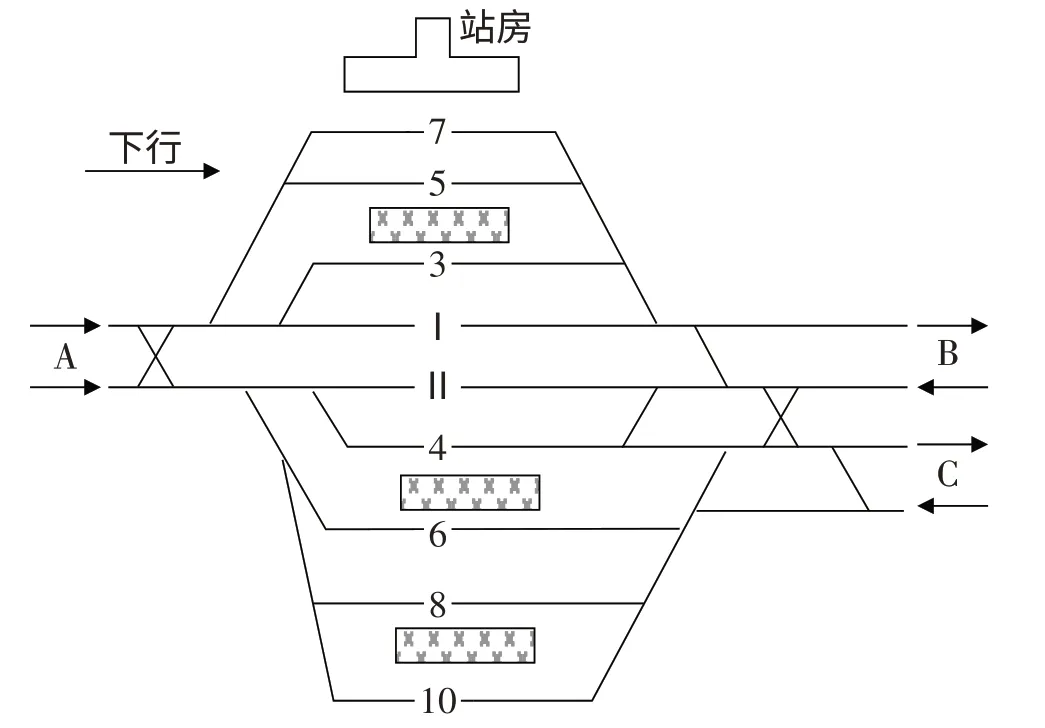
图1 某客运站平面布置简图

一个高峰时间段（07：00-08：30）内有26 列车需要安排股道，且车站作业最小间隔时间为3.0 min，列车到达作业和出发作业均为4.0 min，采用JAVA语言进行编程求解。

4.1 分配方案一 仅考虑目标函数1时，股道具体分配结果如表1所示。

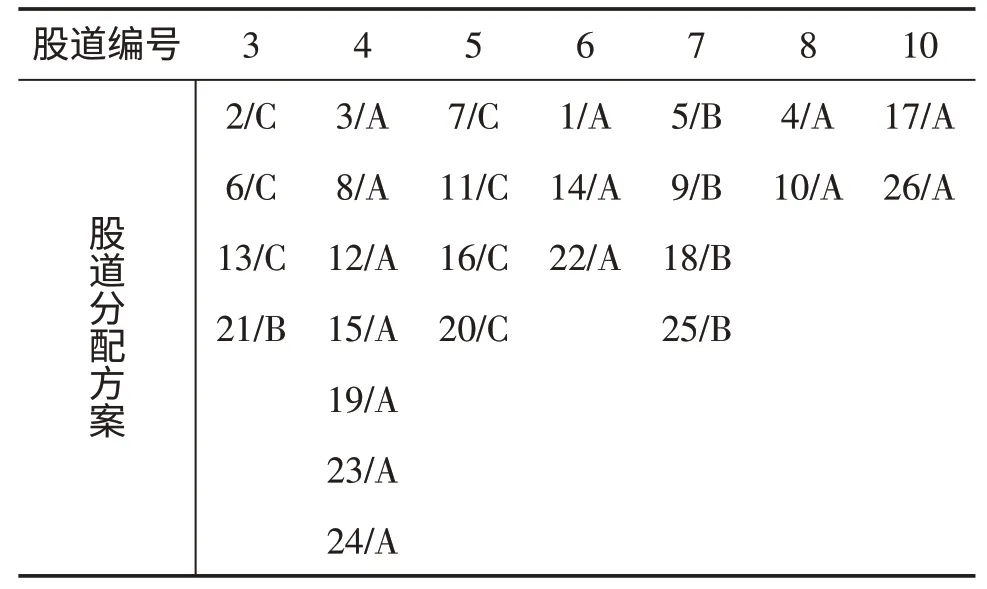
表1 分配方案一（列车编号/去向）

该方案中目标函数1 的值为2 032，目标函数2的值为1 579。

4.2 分配方案二 同时考虑目标函数1 和目标函数2，算法求解的股道分配方案如表2所示：

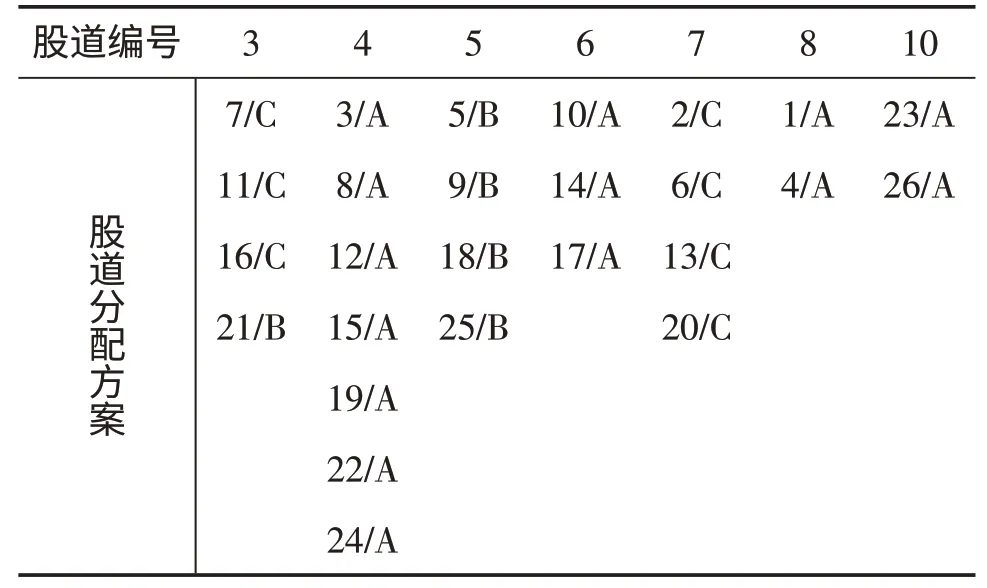
表2 分配方案二（列车编号/去向）

该方案的目标函数1 的值为2 053，目标函数2的值为417.33。

从以上2个分配方案对比可以看出，各列车均按照可利用的股道集使用股道，A 去向的列车选择股道4，6，8，10，B 去向和C 去向列车选择股道3，5，7；上下行靠近站房的股道4，5，7 安排的列车较多，方便旅客乘降；每个股道的列车数为2～7 列，从数量上看比较均衡。与分配方案一相比，分配方案二的目标函数1 值仅大了20，但是目标函数2 值却小了很多。因此，分配方案二比较均衡。

5 结束语

本文从车站的高峰期和低谷期情况考虑，分别建立了多目标的股道分配均衡性模型。高峰期以股道占用时间和股道空闲间隔时间均衡性为优化目标，建立股道分配均衡性模型；而低谷期以方便旅客乘降为优化目标，建立股道分配均衡性模型。而后，采用遗传算法对模型进行求解，该算法可以缩小搜索空间，提高模型的求解效率。最后，以某一客运站高峰时期对模型进行了验证，通过2个分配方案的对比可以看出，评价车站股道使用方案的均衡性，要综合考虑股道占用时间和股道空闲时间间隔的均衡性2个方面。

〔1〕雷定猷，王 栋，刘明翔.客运站股道运用优化模型及算法〔J〕.交通运输工程学报，2007，7（5）：84-87.

〔2〕林志安，潘玲巧.铁路客运站到发线分配问题研究〔J〕.铁路运输与经济，2010，32（10）：58-61.

〔3〕贾文峥，毛保华，何天健，刘海东.大型客运站股道分配问题的模型与算法〔J〕.铁道学报，2010，32（2）：8-13.

〔4〕Carey.A model and strategy for train pathing with choice of lines，platforms and routes〔J〕.Transportation Research B.1994.

〔5〕Zwaneveld，Kroon.Routing trains through a railway station based on a node packing model〔J〕European Journal of Operational Research，1999.

〔6〕谢楚农，黎新华.铁路客运站到发线运用优化研究〔J〕.中国铁道科学，2004，25（5）：130-133.

〔7〕鲁工圆.客运专线车站作业仿真系统的研究及应用〔D〕.成都：交通运输规划与管理，2007.

〔8〕吕红霞.铁路大型客运站作业计划智能编制的优化技术和方法研究〔D〕.成都：交通信息工程与控制.