基于阻塞流理论的客运站阻塞状态研究

2013-11-12冯丽萍鲍晶晶

铁道运营技术 2013年4期

冯丽萍，鲍晶晶

（西南交通大学交通运输与物流学院，博士研究生，四川成都 610031）

旅客列车开行方案的编制是以前期的交通起止点客流量调查结果为基础的，但根据文献〔1〕的研究成果，空间差异是空间运输联系的直接原因，同时也决定着空间联系的演变。因此尽管开行方案的制定是以客流调查为依据的，但随着不同空间的相对势能的变化，客流量也随之动态的变化。随着时间的推移，客流与前期调查的结果相差越来越大时，需进行开行方案的调整。在实际工作中，一般是以现行运行图中开行的旅客列车或相似条件下的其他线路运营经验为基础，根据计划客流，确定加开的、慢改快、快改特快、短变长的旅客列车，综合形成一个新的旅客列车开行方案〔2〕。

本文基于阻塞流相关理论知识为基础，利用现有列车运行图铺画状态下客流在各车站的统计数据，对各车站的阻塞状态及阻塞程度进行判断，为编制新的开行方案提供依据，并以阻塞状态为基础提出阻塞消解的办法，为开行方案的优化提供思路。

1 阻塞流理论简介

阻塞流理论是1992年由南京航空航天大学宁宣熙教授受现代交通阻塞现象的启发提出阻塞流动的问题，然后经过多年的系统研究发展而来的，前多用于解决城市交通网络阻塞问题〔3，4，5〕。

在该理论中，交通网络中的阻塞可分为局部阻塞和整个网络的阻塞或网络阻塞2种。所谓局部阻塞是指网络顶点处的阻塞现象。当这种阻塞发生时，在这些阻塞点及相应的弧内集聚过多的流量，使局部成为不可行流，这时网络的总流量变小，如图1中顶点v3、v4处被阻塞8个单位流量。

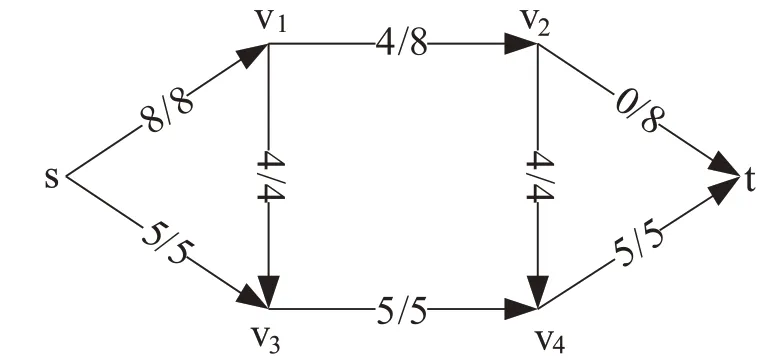
图1 局部阻塞示意图

这种阻塞状态正是本文所探讨的阻塞。为描述顶点处的阻塞状态，现引入容差的概念。所谓顶点A的容差ΦA是指所有以A为始点的有向弧的容量总和与所有以A为终点的有向弧容量总和之差，即

式中，vi（a）为弧a 的始点，vj（a）为弧a 的终点。当ΦA＜0 时，说明A 点处出现阻塞状态，需要进行调整；反之，说明该点并未发生阻塞。

因此，本文对通过能力分别从铁路运输生产部门的角度和旅客角度出发做出如下定义：以往对通过能力的定义称为生产通过能力，用以反映运行图能力利用情况；而旅客通过能力是指在既有的运行图铺画方式下，任意两车站之间所能输送的最大旅客数量，用以描述供给量与需求量之间的匹配情况。本文中对车站阻塞状态的研究就是基于旅客通过能力的。

2 基于列车运行图建立路网拓扑模型

2.1 模型建立的前提假设本文中建立的路网拓扑模型是基于实际铁路网和现行的列车运行图建立的拓扑模型。即以车站为点，若运行图中存在联系两站之间的运行线则将两者相连。现对模型建立的前提假设说明如下：

1）所有车次成对行车，且对于到达车站后乘对向列车离开的折返客流不予考虑。

2）按照建模连续性原则，为保证旅客在路网运输过程中不会凭空消失，在每个车站点设置对应虚拟点。实点与虚拟点之间的联系代表进入本站参加运输和到达本站完成运输或换乘到其他运输方式的过程。

3）对于在铁路内部换乘的旅客，将换乘站看作是第1次运输完成的地方，也是第2次开始运输的地方。而对于内部换乘所需要的两车次之间的时间间隔是否合理等则不予以考虑。

此外，在铁路运输生产中，通过能力是指在采用一定类型的机车车辆和一定的行车组织方法条件下，铁路区段的各种固定设备，在单位时间内（通常指一昼夜）所能通过的最多列车数或对数〔6〕。即在目前的研究中，多以列车数作为通过能力大小的量化方式。但通过能力反映到旅客身上即为在一定时间段内铁路所能运送的最大旅客数量，这才是旅客最关心的直接问题。而且在路网中，客运站作为不同车次列车的接续点或运输组织的中断点，而正因为这种中断使得以车站为分界点，若车站所衔接的各方向所聚散旅客的数量不匹配，就会造成运输组织的不顺畅，即发生车站阻塞现象。因此本文采用的是基于旅客发送数量的通过能力。

2.2 模型建立及变量设置现假设路网中共有6个车站，下行列车开行方案如表1所示，则可构建路网拓扑模型（见如图2）。按照以上原则，在对车站1进行阻塞判断时，则以广义到达客流量（包括完成一次运输的到达和到达车站开始乘车的到达客流）与广义出发客流量（包括到达车站后离开车站的客流和乘坐列车离开车站的客流）之差，判断车站是否发生阻塞。若发生阻塞，还可以任一车次为对象，判断该车次列车对车站聚散客流的变化的抗阻塞能力，从而分析阻塞发生的原因，提出消解方案。

表1 列车停车方案表

图2 网络拓扑模型示意图

现对模型中的变量说明如下：对路网内各客运站在除节假日之外一定时间内（如一个月）的客流进行统计，得到在一昼夜内以任一车站n 为运输始点和运输终点的客流平均值分别为，在统计周期内客流以平均值为基准的上下波动区间分别为（α-，α+）和（β-，β+），其中，在以车站n 为终点站的客流中以n 为换乘站的比例为，在以车站n 为起点站的客流中是进行第一次运输的客流比例为。设车站n 共连接M 方向，任一方向的在一昼夜的旅客通过能力为，尽管由于成对行车，各方向的生产通过能力是相同的，但旅客通过能力不尽然。因此将各方向一昼夜的旅客通过能力按上下行分为。

3 车站阻塞状态判断及消解

以车站1为例，设其统计数据如表2所示，路网中任意两点之间以停站次数最少为基准的最短路径如表3所示，在客运站1上在各方向上的分担率如表4所示。现对1车站的阻塞状态分析如下。

表2 车站1的统计数据表

表3 客运站间最短路径表

表4 各方向分担率

3.1 阻塞状态判断根据容差思想，对客运站的阻塞能力判断即是对车站的广义到达客流与广义出发客流的匹配情况进行考察。当前者大于后者时，可认为在车站1由于运输衔接不合理或旅客通过能力不足导致铁路客流流失；反之，则认为铁路衔接组织良好，但也要注意旅客通过能力的阻塞程度问题。对于车站1阻塞状态的判断可依据下式

根据计算结果可知，在客运站1 广义到达客流大于广义出发客流，客运站1存在阻塞现象。此外，考虑各方向上的旅客通过能力计算与车站1相连各方向旅客产生量与旅客通过能力之间的匹配情况。计算结果如表5所示。

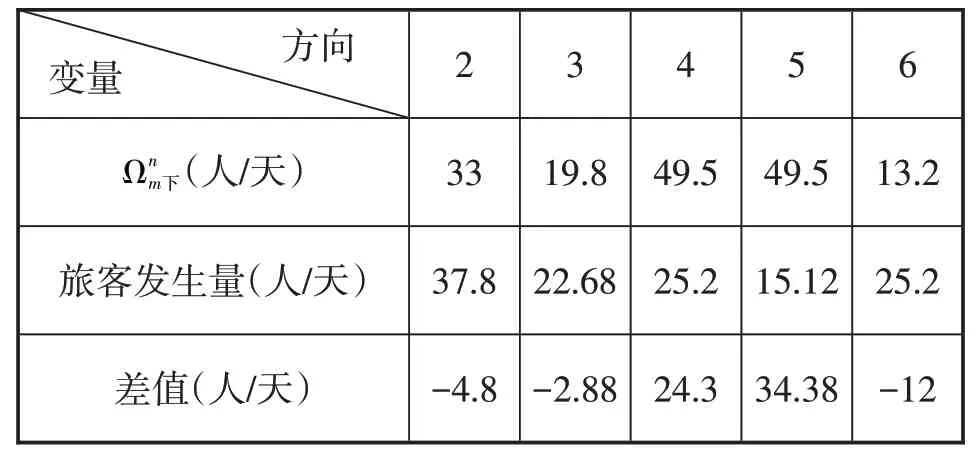
表5 各方向旅客通过能力匹配情况

从表格中可以看出与客运站1 连接的2、3、6 方向的阻塞是车站阻塞的主因，且各方向旅客通过能力分配不均衡。

3.2 各方向抗阻塞能力检查在上述的车站阻塞状态判断中所采用的数据均为统计时间内的平均值，且客流量在各方向的分担率是固定不变的，因此虽然能够反映出车站在统计时间内的总体情况，但并不能说明其动态变化。因此须对各方向进行抗阻塞检查。所谓抗阻塞检查是指当客流量在其波动范围内随机变化时，与车站衔接各方向的旅客通过能力与所分担客流量之间的匹配情况检查。对于车站1，当分别在波动区间（α-，α+）、（β-，β+）内变化时，客运站1及与其相连各方向的阻塞情况如表6所示。

从表6 可以看出，当客流随机波动时，客运站1在5 次随机试验中均表现为阻塞，其抗阻塞能力较差。在与客运站1相连的各方向上4、5方向表现为较强的抗阻塞能力，而2、3、6 方向的抗阻塞能力不相上下，都处于抗阻塞能力较为薄弱的状态。

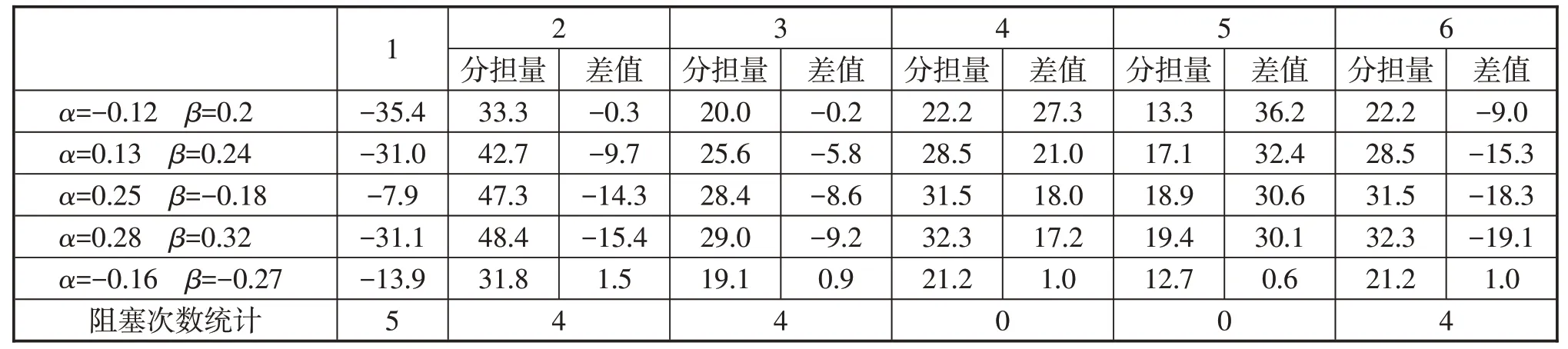
表6 随机波动客流下的阻塞状态判断（单位：人/天）

3.3 阻塞消解方案通过车站阻塞状态的判断，依据对与车站相连各方向抗阻塞能力的检查，可以提出车站阻塞的消解方案。所谓消解就是通过对开行方案的调整，将与车站衔接方向中抗阻塞能力较差或阻塞程度较高的方向中的客流量通过合理设置到发时间、减少停站次数等措施诱导乘客转移到抗阻塞能力较强的方向上或增强该方向上的生产通过能力。

在本文设置的案例中，车站阻塞状态主要是由于在与客运站相衔接的2、3、6 方向上的阻塞引起的。而依据表3，车站1与2、3、6衔接的最短路径分别为：I/VII、II、V，为此可以通过在1-2、1-3、1-6 间开行短途直达列车增大生产通过能力，从而提高旅客通过能力的抗干扰能力。也可以通过在III、IV方案中在2、3、6中增加停站的方式，吸引2、3、6方向的客流转移到抗阻塞能力较强的4、5方向上。但需注意的是，阻塞消解的过程是诱导客流均衡分配的过程而不是简单的阻塞转移。即在诱导过程中，应主因4、5 方向的抗阻塞能力在客流转移过程中的变化，不能以4、5方向的阻塞换取2、3、6方向的能力富余。