突发中断条件下轨道交通客流疏运路径集模型

肖冠宇

（西南交通大学 交通运输与物流学院，硕士研究生，四川 成都 610031）

由于设备故障、自然灾害以及人为事故等无法预知的各种原因，城市轨道交通路网在运营过程中不可避免的会发生突发事故，导致路网中的区间或者车站运营中断，造成大量的出行乘客的滞留，甚至造成严重的财产损失乃至重大伤亡事故。本文以突发事故中路网的某区间或者车站发生中断为前提条件，综合铁路运输组织、图论以及复杂网络等相关的理论及方法，构建此种情况下应急的客流疏运路径集模型，研究此种条件下滞留乘客的应急疏运问题，从而保证旅客安全、顺利地疏散和出行。

1 突发中断的轨道交通路网模型描述

1.1 客流分析 本文研究的突发中断对路网所造成的直接影响，就是路网中的线路上某中断点所对应的某个区间列车运行暂时中断，但是路网中的客流通常不会发生大的突变，仅仅是路网受到了影响的区段以及线路的供给能力或者通过能力发生了变化。因此，客流分析的问题就集中在各种OD 的客流在受影响的路网中如何重新进行分配〔1〕。此时的客流可以分为2大类：

1）直接放弃轨道交通方式转而选择其他交通方式出行的客流。

2）在轨道交通路网内选择其他路径从而完成出行的客流。

鉴于在网络化运营的轨道交通系统中，普通的突发中断事件对于整体路网的连通可靠性不会造成质变的影响，因此以绕行其他路径的出行方式，通常可以顺利促成在应急情况下这类客流的出行目的。综上所述，本文将着手研究针对于第2 类客流应急疏运的路径模型问题。

1.2 中间折返站及应急交路 在中断情况突发之时，对于受到突发中断区间影响的客流的疏散，可以考虑启用应急的城市道路公交联动。但是，考虑到轨道交通自有的运量大以及相对准时等固有的优势，在具备中间折返条件的线路上开行应急的临时交路，应当成为疏解客流的首要措施。

中间折返站作为轨道交通路网的重要车站，其设计与建造在一定程度上影响乃至决定着整个线路的运输能力以及工程造价等，其配线的铺设也是轨道交通线路设计的重点问题。在路网发生突发的客流滞留时，有效利用这些中间折返站开行临时交路，可以有效、快速地疏解滞留拥堵的客流〔2〕。突发中断下开行的应急交路如图1所示。

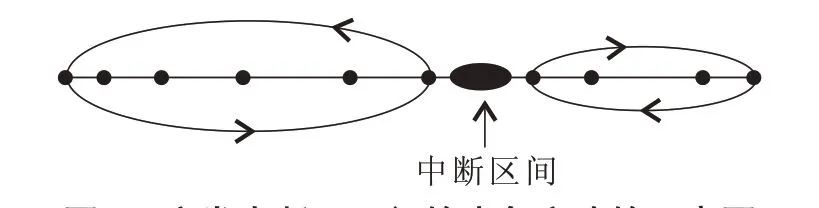
图1 突发中断下开行的应急交路的示意图

《地铁设计规范》（GB 50157-2003）规定：当两个具备临时停车条件的车站相距较远时，根据运营需要，宜在沿线每隔3～5个车站加设停车线或渡线。因此，对于本文所研究的应急交路来说，对于中间折返站数目的最低要求为某条线路上的每10个车站中至少有2个车站具备列车折返能力。以此为基础，在突发中断事故的应急处置中，轨道交通行车可以根据停车线、渡线等的设置情况，采取组织临时的应急交路以维持路网的局部连通性。

2 模型建立

2.1 模型基础及相关理论

2.1.1 路网拓扑结构模型 中断情况下的路网拓扑结构可以变化为如下2个部分：其一，中断区间所在的线路，按照应急的临时交路开行列车，中断的区间等效于被从路网中去除；其二，其他的线路的拓扑结构保持不变，如图2所示。

图2 突发中断条件下路网拓扑结构示意图

此时的待疏散的客流，主要是原始出行的最短径路包含中断区间或者出行的终点站位于中断区间内的客流。因此，基于此时形成的新的路网拓扑结构，此时客流疏散的主要问题即可归结为，求解从中间折返站s 站到中间折返站t 站以及其后各站的可行路径集，从而按照最优路径、次优路径等分流疏散滞留的乘客。

2.1.2 路网有向图描述 根据图论的相关理论，有向图是由一个非空的有限集合V和集合V中的某些元素的有序对的集合A 所构成的二元组，可以记为G=（V，A）。A 中的每一个元素ak=（vi，vj）表示图G 中的一条从vi到vj的弧，并且vi被称为ak的尾，vj被称为ak的头，并称ak为vi的入弧，为vj的出弧〔3〕。要求解最优可行路径问题，首先就要建立轨道交通路网拓扑结构的有向图模型。将车站建立为网络中的节点，将线路的上下行建立成节点间的有向边，与相应的节点对应。

2.2 最优可行路径集模型建立 如上所述，以中断后生成的新的路网的拓扑结构模型为基础，以中间折返站vs为起点，中间折返站vt为终点，定义为两站间的可行路径集合，其中表示从节点vs到达节点vt的第k最优径路，λ（s，t）表示从节点vs到节点vt的所求得的总的最优径路的数量。表示节点vs到节点vt的第k条最优路径的总出行阻抗。集合Rs，t满足

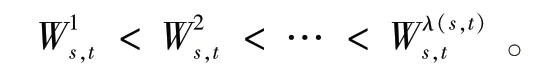
以aij表示网络模型中从i 点到j 点的边，ωij表示该条边上的权值，决策变量用来表示弧aij是否在径路上：

由此，求解突发中断下路网的最优可行路径集的目标函数可以表示为：

2.3 模型说明 在客流的OD 确定的情况下，广义的出行时间成为衡量出行阻抗的主要标准。而从轨道交通管理者的角度，在突发情况下，客流的疏散时间也必然成为首要的考虑对象。用Aij表示列车在车站i 与j 的运行时间，Bk表示乘客在车站k 所花费的时间，则有：

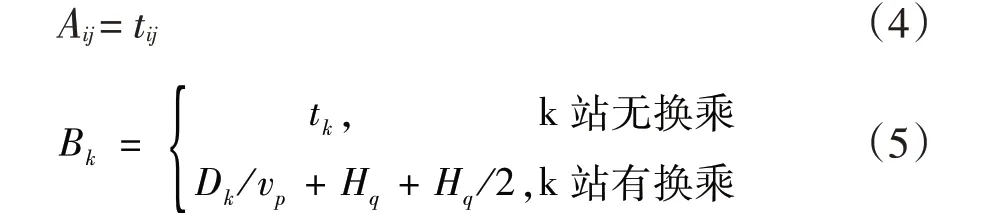
其中，tij为列车在车站i 与j 之间的运行时间，tk为列车在车站k 的停站时间，Dk为换乘站换乘时乘客的走行距离，vp表示乘客的走行速度，Hq表示所换乘的线路的列车在该站的停站时间。则有：

在突发中断事件中，如果乘客通过某站点时不换乘，可将该站点的权值置为0；如果发生换乘，则需要根据换乘所需时间进行相应的赋值处理。

3 求解算法

本模型与传统的K 最短路算法〔4〕有所不同，因此需要设计针对性的算法进行求解。

3.1 换乘站的处理方法 很明显，换乘站区别于普通的中间站点，而且对于最优路径、次优路径等的生成起到关键的作用。为了恰当地处理换乘站在路网模型中的权重问题，本文将这些换乘站拆分成若干个虚拟的站点，彼此之间用虚拟的边相连，然后，按照换乘时间或者直接通过的时间，将这些虚拟的边进行赋值，如图3所示。

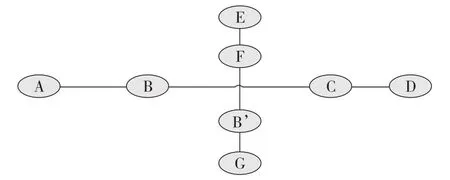
图3 换乘站B站的处理方法示意图

3.2 求解方法及步骤 在交通领域的相关研究中，图论中的Dijkstra 算法〔5〕是较为常用的算法。在本文的最优路径集模型中，客流的疏散时间成为衡量路径的主要标准。基于此，本文使用改进了的删除算法〔6〕，与传统的Dijkstra 算法相结合来求解此模型，具体方法如下：

1）开始求解前，给网络中的每一个节点i 设置两个参数，标号li和紧前节点pi，li表示从根节点s 开始到i 的最小阻抗，pi表示沿最优路径到达节点i 且最靠近节点i的节点。

2）利用Dijkstra 算法的思路求得在中断后的路网拓扑结构中的从s站到t站的最优路径。

3）进一步结合改进的删除算法，求得次优路径，再次优路径等，具体步骤如下：

步骤1：标记上一步的节点s 到t 的最优路径为pk，k=1。

步骤2：若k 小于λ（s，t），并且仍存在候选路径时，令当前路径p=pk，转步骤3；否则，程序结束。

步骤3：找到当前路径p中从第一个节点开始的首个入度（进入某节点的路径数量）大于1 的节点，标记为vh。为vh构建一个扩展节点vh，并将该扩展节点纳入V中，并记vi=vh+1。

步骤4：将路径p中的所有的从vi开始的后续节点记为vj，添加vj的扩展节点vj到点集V 中。除了路径p 中各个vj的前一个节点vj-1之外，分别连接一条从vj的前驱结点到其扩展节点vj的边，边的权值不变，计算从s到vj的最短路径。

步骤5：更新当前的最短路径树，求得从s到t的当前扩展节点tk之间的最短路径为第k 条最短路径。令k=k+1，转至步骤2继续计算。

4 结束语

本文建立了突发中断条件下的轨道交通路网的应急客流疏运的最优可行路径集模型，分析了模型的参数及限制条件，并设计了针对性的求解算法。轨道交通的运营部门可以在应急处置中按照该模型的求解结果分流、疏散中断区间内的滞留客流，调节其他线路列车的应急开行方案，从而保证旅客安全、顺利地疏散和出行。

〔1〕王志强.城市轨道交通应急决策辅助技术研究〔D〕.同济大学博士学位论文，2008.

〔2〕刘华，周天星.城市轨道交通折返站辅助配线设计研究〔J〕.城市轨道交通，2007，2：57-59.

〔3〕苏娟.城市轨道交通客流分配研究〔D〕.北京交通大学硕士学位论文，2009.

〔4〕石宁，贾迎琳.带约束条件的K 最短问题〔J〕.中大管理研究，2009，4（1）：34-56.

〔5〕Dijkstra E W.A note on two problems in connection with graphs〔J〕.Numeric Mathematics，1959（1）：269-271.

〔6〕徐瑞华，罗钦，高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究〔J〕.铁道学报，2009，31（2）：110-114.